AUTHORS:
This module defines the mod  Steenrod algebra
Steenrod algebra
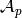 , some of its properties, and ways to
define elements of it.
, some of its properties, and ways to
define elements of it.
From a topological point of view, 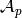 is the
algebra of stable cohomology operations on mod
is the
algebra of stable cohomology operations on mod  cohomology; thus for any topological space
cohomology; thus for any topological space  , its mod
, its mod
 cohomology algebra
cohomology algebra 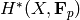 is a
module over
is a
module over 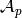 .
.
From an algebraic point of view, 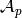 is an
is an
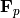 -algebra; when
-algebra; when 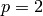 , it is
generated by elements
, it is
generated by elements 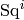 for
for 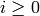 (the Steenrod squares), and when
(the Steenrod squares), and when  is odd, it is
generated by elements
is odd, it is
generated by elements 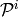 for
for
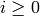 (the Steenrod reduced `p`th powers)
along with an element
(the Steenrod reduced `p`th powers)
along with an element 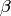 (the
mod `p` Bockstein). The Steenrod algebra is graded:
(the
mod `p` Bockstein). The Steenrod algebra is graded:
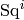 is in degree
is in degree  for each
for each
 ,
, 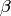 is in degree 1, and
is in degree 1, and
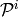 is in degree
is in degree 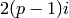 .
.
The unit element is 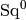 when
when 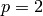 and
and
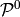 when
when  is odd. The generating
elements also satisfy the Adem relations. At the prime 2, these
have the form
is odd. The generating
elements also satisfy the Adem relations. At the prime 2, these
have the form
![\text{Sq}^a \text{Sq}^b = \sum_{c=0}^{[a/2]} \binom{b-c-1}{a-2c} \text{Sq}^{a+b-c} \text{Sq}^c.](../../_images/math/996c408329c1538831d0a2619d5dd80c9f7213c3.png)
At odd primes, they are a bit more complicated. See Steenrod and
Epstein [SE] for full details. These relations lead to the
existence of the Serre-Cartan basis for
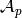 .
.
The mod  Steenrod algebra has the structure of a Hopf
algebra, and Milnor [Mil] has a beautiful description of the dual,
leading to a construction of the Milnor basis for
Steenrod algebra has the structure of a Hopf
algebra, and Milnor [Mil] has a beautiful description of the dual,
leading to a construction of the Milnor basis for
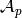 . In this module, elements in the Steenrod
algebra are represented, by default, using the Milnor basis.
. In this module, elements in the Steenrod
algebra are represented, by default, using the Milnor basis.
See the documentation for SteenrodAlgebra for many more details and examples.
REFERENCES:
Bases: sage.structure.factory.UniqueFactory
The mod  Steenrod algebra
Steenrod algebra
INPUT:
OUTPUT:
 Steenrod algebra with given basis
Steenrod algebra with given basisThis returns the mod  Steenrod algebra, elements of which are
printed using basis.
Steenrod algebra, elements of which are
printed using basis.
EXAMPLES:
Some properties of the Steenrod algebra are available:
sage: A = SteenrodAlgebra(2)
sage: A.ngens() # number of generators
+Infinity
sage: A.gen(5) # 5th generator
Sq(32)
sage: A.order()
+Infinity
sage: A.is_finite()
False
sage: A.is_commutative()
False
sage: A.is_noetherian()
False
sage: A.is_integral_domain()
False
sage: A.is_field()
False
sage: A.is_division_algebra()
False
sage: A.category()
Category of algebras over Finite Field of size 2
There are methods for constructing elements of the Steenrod algebra:
sage: A2 = SteenrodAlgebra(2); A2
mod 2 Steenrod algebra
sage: A2.Sq(1,2,6)
Sq(1,2,6)
sage: A2.Q(3,4) # product of Milnor primitives Q_3 and Q_4
Sq(0,0,0,1,1)
sage: A2.pst(2,3) # Margolis pst element
Sq(0,0,4)
sage: A5 = SteenrodAlgebra(5); A5
mod 5 Steenrod algebra
sage: A5.P(1,2,6)
P(1,2,6)
sage: A5.Q(3,4)
Q_3 Q_4
sage: A5.Q(3,4) * A5.P(1,2,6)
Q_3 Q_4 P(1,2,6)
sage: A5.pst(2,3)
P(0,0,25)
You can test whether elements are contained in the Steenrod algebra:
sage: w = Sq(2) * Sq(4)
sage: w in SteenrodAlgebra(2)
True
sage: w in SteenrodAlgebra(17)
False
Different bases for the Steenrod algebra:
There are two standard vector space bases for the mod  Steenrod algebra: the Milnor basis and the Serre-Cartan basis. When
Steenrod algebra: the Milnor basis and the Serre-Cartan basis. When
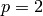 , there are also several other, less well-known,
bases. See the documentation for the function
‘steenrod_algebra_basis’ for full descriptions of each of the
implemented bases.
, there are also several other, less well-known,
bases. See the documentation for the function
‘steenrod_algebra_basis’ for full descriptions of each of the
implemented bases.
This module implements the following bases at all primes:
It implements the following bases when 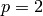 :
:
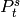 -bases.
-bases.When defining a Steenrod algebra, you can specify a basis. Then elements of that Steenrod algebra are printed in that basis
sage: adem = SteenrodAlgebra(2, 'adem')
sage: x = adem.Sq(2,1) # Sq(-) always means a Milnor basis element
sage: x
Sq^{4} Sq^{1} + Sq^{5}
sage: y = Sq(0,1) # unadorned Sq defines elements w.r.t. Milnor basis
sage: y
Sq(0,1)
sage: adem(y)
Sq^{2} Sq^{1} + Sq^{3}
sage: adem5 = SteenrodAlgebra(5, 'serre-cartan')
sage: adem5.P(0,2)
P^{10} P^{2} + 4 P^{11} P^{1} + P^{12}
You can get a list of basis elements in a given dimension:
sage: A3 = SteenrodAlgebra(3, 'milnor')
sage: A3.basis(13)
(Q_1 P(2), Q_0 P(3))
As noted above, several of the bases (‘arnon_a’, ‘wall’, ‘comm’)
have alternate, longer, representations. These provide ways of
expressing elements of the Steenrod algebra in terms of the
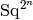 .
.
sage: A_long = SteenrodAlgebra(2, 'arnon_a_long')
sage: A_long(Sq(6))
Sq^{1} Sq^{2} Sq^{1} Sq^{2} + Sq^{2} Sq^{4}
sage: SteenrodAlgebra(2, 'wall_long')(Sq(6))
Sq^{2} Sq^{1} Sq^{2} Sq^{1} + Sq^{2} Sq^{4}
sage: SteenrodAlgebra(2, 'comm_deg_long')(Sq(6))
s_{1} s_{2} s_{12} + s_{2} s_{4}
Testing unique parents:
sage: S0 = SteenrodAlgebra(2)
sage: S1 = SteenrodAlgebra(2)
sage: S0 is S1
True
This is an internal function that is used to ensure unique parents. Not for public consumption.
EXAMPLES:
sage: SteenrodAlgebra.create_key()
(2, 'milnor')
This is an internal function that is used to ensure unique parents. Not for public consumption.
EXAMPLES:
sage: SteenrodAlgebra.create_object(1,(11,'milnor'))
mod 11 Steenrod algebra
Bases: sage.rings.ring.Algebra
The mod  Steenrod algebra.
Steenrod algebra.
Users should not call this, but use the function ‘SteenrodAlgebra’ instead. See that function for extensive documentation.
EXAMPLES:
sage: sage.algebras.steenrod_algebra.SteenrodAlgebra_generic()
mod 2 Steenrod algebra
sage: sage.algebras.steenrod_algebra.SteenrodAlgebra_generic(5)
mod 5 Steenrod algebra
sage: sage.algebras.steenrod_algebra.SteenrodAlgebra_generic(5, 'adem')
mod 5 Steenrod algebra
The element 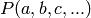
INPUT:
OUTPUT: element of the Steenrod algebra given by the single basis element P(a, b, c, ...)
Note that at the prime 2, this is the same element as
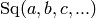 .
.
EXAMPLES:
sage: A = SteenrodAlgebra(2)
sage: A.P(5)
Sq(5)
sage: B = SteenrodAlgebra(3)
sage: B.P(5,1,1)
P(5,1,1)
The element 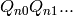 , given by specifying the
subscripts.
, given by specifying the
subscripts.
INPUT:
OUTPUT: The element 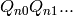
Note that at the prime 2, 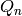 is the element
is the element
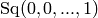 , where the 1 is in the
, where the 1 is in the
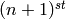 position.
position.
Compare this to the method ‘Q_exp’, which defines a similar element, but by specifying the tuple of exponents.
EXAMPLES:
sage: A2 = SteenrodAlgebra(2)
sage: A5 = SteenrodAlgebra(5)
sage: A2.Q(2,3)
Sq(0,0,1,1)
sage: A5.Q(1,4)
Q_1 Q_4
sage: A5.Q(1,4) == A5.Q_exp(0,1,0,0,1)
True
The element 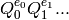 , given by
specifying the exponents.
, given by
specifying the exponents.
INPUT:
OUTPUT: The element 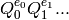
Note that at the prime 2, 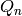 is the element
is the element
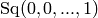 , where the 1 is in the
, where the 1 is in the
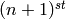 position.
position.
Compare this to the method ‘Q’, which defines a similar element, but by specifying the tuple of subscripts of terms with exponent 1.
EXAMPLES:
sage: A2 = SteenrodAlgebra(2)
sage: A5 = SteenrodAlgebra(5)
sage: A2.Q_exp(0,0,1,1,0)
Sq(0,0,1,1)
sage: A5.Q_exp(0,0,1,1,0)
Q_2 Q_3
sage: A5.Q(2,3)
Q_2 Q_3
sage: A5.Q_exp(0,0,1,1,0) == A5.Q(2,3)
True
Basis for self in dimension n
INPUT:
OUTPUT:
EXAMPLES:
sage: A3 = SteenrodAlgebra(3)
sage: A3.basis(13)
(Q_1 P(2), Q_0 P(3))
sage: SteenrodAlgebra(2, 'adem').basis(12)
(Sq^{12},
Sq^{11} Sq^{1},
Sq^{9} Sq^{2} Sq^{1},
Sq^{8} Sq^{3} Sq^{1},
Sq^{10} Sq^{2},
Sq^{9} Sq^{3},
Sq^{8} Sq^{4})
The ith generator of the Steenrod algebra.
INPUT:
OUTPUT: the ith generator of the Steenrod algebra
The 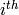 generator is
generator is 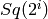 at the prime 2;
when
at the prime 2;
when  is odd, the 0th generator is
is odd, the 0th generator is
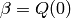 , and for
, and for 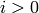 , the
, the 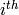 generator is
generator is 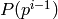 .
.
EXAMPLES:
sage: A = SteenrodAlgebra(2)
sage: A.gen(4)
Sq(16)
sage: A.gen(200)
Sq(1606938044258990275541962092341162602522202993782792835301376)
sage: B = SteenrodAlgebra(5)
sage: B.gen(0)
Q_0
sage: B.gen(2)
P(5)
List of generators for the Steenrod algebra. Not implemented (mainly because the list of generators is infinite).
EXAMPLES:
sage: A3 = SteenrodAlgebra(3, 'adem')
sage: A3.gens()
...
NotImplementedError: 'gens' is not implemented for the Steenrod algebra.
The Steenrod algebra is not commutative.
EXAMPLES:
sage: A = SteenrodAlgebra(3)
sage: A.is_commutative()
False
The Steenrod algebra is not a division algebra.
EXAMPLES:
sage: A = SteenrodAlgebra(3)
sage: A.is_division_algebra()
False
The Steenrod algebra is not a field.
EXAMPLES:
sage: A = SteenrodAlgebra(3)
sage: A.is_field()
False
The Steenrod algebra is not finite.
EXAMPLES:
sage: A = SteenrodAlgebra(3)
sage: A.is_finite()
False
The Steenrod algebra is not an integral domain.
EXAMPLES:
sage: A = SteenrodAlgebra(3)
sage: A.is_integral_domain()
False
The Steenrod algebra is not noetherian.
EXAMPLES:
sage: A = SteenrodAlgebra(3)
sage: A.is_noetherian()
False
Number of generators of the Steenrod algebra.
This returns infinity, since the Steenrod algebra is infinitely generated.
EXAMPLES:
sage: A = SteenrodAlgebra(3)
sage: A.ngens()
+Infinity
The Steenrod algebra has infinite order.
EXAMPLES:
sage: A = SteenrodAlgebra(3)
sage: A.order()
+Infinity
The Margolis element 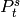 .
.
INPUT:
OUTPUT: element of the Steenrod algebra
This returns the Margolis element 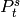 of the mod
of the mod
 Steenrod algebra: the element equal to
Steenrod algebra: the element equal to
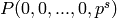 , where the
, where the 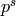 is in position
is in position
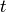 .
.
EXAMPLES:
sage: A2 = SteenrodAlgebra(2)
sage: A2.pst(3,5)
Sq(0,0,0,0,8)
sage: A2.pst(1,2) == Sq(4)*Sq(2) + Sq(2)*Sq(4)
True
sage: SteenrodAlgebra(5).pst(3,5)
P(0,0,0,0,125)
Bases: sage.algebras.steenrod_algebra.SteenrodAlgebra_generic
The mod 2 Steenrod algebra.
Users should not call this, but use the function ‘SteenrodAlgebra’ instead. See that function for extensive documentation. (This differs from SteenrodAlgebra_generic only in that it has a method ‘Sq’ for defining elements.)
Milnor element 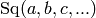 .
.
INPUT:
OUTPUT: element of the Steenrod algebra
This returns the Milnor basis element
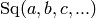 .
.
EXAMPLES:
sage: A = SteenrodAlgebra(2)
sage: A.Sq(5)
Sq(5)
sage: A.Sq(5,0,2)
Sq(5,0,2)
Entries must be non-negative integers; otherwise, an error results.
Return canonical basis named by string basis at the prime p.
INPUT:
OUTPUT:
EXAMPLES:
sage: sage.algebras.steenrod_algebra.get_basis_name('adem', 2)
'serre-cartan'
sage: sage.algebras.steenrod_algebra.get_basis_name('milnor', 2)
'milnor'
sage: sage.algebras.steenrod_algebra.get_basis_name('MiLNoR', 5)
'milnor'
sage: sage.algebras.steenrod_algebra.get_basis_name('pst-llex', 2)
'pst_llex'