AUTHORS:
This code is partly based on Sage code by David Kohel from 2005.
TESTS:
Pickling test:
sage: Q.<i,j,k> = QuaternionAlgebra(QQ,-5,-2)
sage: Q == loads(dumps(Q))
True
There are three input formats:
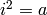 ,
, 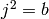 ,
,  .
.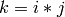 .
.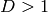 is a squarefree integer.
is a squarefree integer.EXAMPLES:
QuaternionAlgebra(a, b) - return quaternion algebra over the
smallest field containing the nonzero elements a and b with
generators i, j, k with 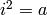 ,
, 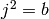 and
and 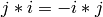 :
:
sage: QuaternionAlgebra(-2,-3)
Quaternion Algebra (-2, -3) with base ring Rational Field
sage: QuaternionAlgebra(GF(5)(2), GF(5)(3))
Quaternion Algebra (2, 3) with base ring Finite Field of size 5
sage: QuaternionAlgebra(2, GF(5)(3))
Quaternion Algebra (2, 3) with base ring Finite Field of size 5
sage: QuaternionAlgebra(QQ[sqrt(2)](-1), -5)
Quaternion Algebra (-1, -5) with base ring Number Field in sqrt2 with defining polynomial x^2 - 2
sage: QuaternionAlgebra(sqrt(-1), sqrt(-3))
Quaternion Algebra (I, sqrt(-3)) with base ring Symbolic Ring
sage: QuaternionAlgebra(0,0)
...
ValueError: a and b must be nonzero
sage: QuaternionAlgebra(GF(2)(1),1)
...
ValueError: a and b must be elements of a field with characteristic not 2
QuaternionAlgebra(K, a, b) - return quaternion algebra over the
field K with generators i, j, k with 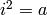 ,
, 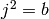 and
and 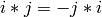 :
:
sage: QuaternionAlgebra(QQ, -7, -21)
Quaternion Algebra (-7, -21) with base ring Rational Field
sage: QuaternionAlgebra(QQ[sqrt(2)], -2,-3)
Quaternion Algebra (-2, -3) with base ring Number Field in sqrt2 with defining polynomial x^2 - 2
QuaternionAlgebra(D) - D is a squarefree integer; returns a rational quaternion algebra of discriminant D:
sage: QuaternionAlgebra(1)
Quaternion Algebra (-1, 1) with base ring Rational Field
sage: QuaternionAlgebra(2)
Quaternion Algebra (-1, -1) with base ring Rational Field
sage: QuaternionAlgebra(7)
Quaternion Algebra (-1, -7) with base ring Rational Field
sage: QuaternionAlgebra(2*3*5*7)
Quaternion Algebra (-22, 210) with base ring Rational Field
If the coefficients  and
and  in the definition of the quaternion
algebra are not integral, then a slower generic type is used for
arithmetic:
in the definition of the quaternion
algebra are not integral, then a slower generic type is used for
arithmetic:
sage: type(QuaternionAlgebra(-1,-3).0)
<type 'sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_rational_field'>
sage: type(QuaternionAlgebra(-1,-3/2).0)
<type 'sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_generic'>
Make sure caching is sane:
sage: A = QuaternionAlgebra(2,3); A
Quaternion Algebra (2, 3) with base ring Rational Field
sage: B = QuaternionAlgebra(GF(5)(2),GF(5)(3)); B
Quaternion Algebra (2, 3) with base ring Finite Field of size 5
sage: A is QuaternionAlgebra(2,3)
True
sage: B is QuaternionAlgebra(GF(5)(2),GF(5)(3))
True
sage: Q = QuaternionAlgebra(2); Q
Quaternion Algebra (-1, -1) with base ring Rational Field
sage: Q is QuaternionAlgebra(QQ,-1,-1)
True
sage: Q is QuaternionAlgebra(-1,-1)
True
sage: Q.<ii,jj,kk> = QuaternionAlgebra(15); Q.variable_names()
('ii', 'jj', 'kk')
sage: QuaternionAlgebra(15).variable_names()
('i', 'j', 'k')
Bases: sage.algebras.quatalg.quaternion_algebra.QuaternionAlgebra_abstract
The quaternion algebra of the form 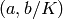 , where
, where 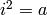 ,
, 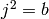 ,
and
,
and 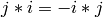 . K is a field not of characteristic 2 and a,
b are nonzero elements of K.
. K is a field not of characteristic 2 and a,
b are nonzero elements of K.
See QuaternionAlgebra for many more examples.
EXAMPLES:
sage: QuaternionAlgebra(QQ, -7, -21) # indirect doctest
Quaternion Algebra (-7, -21) with base ring Rational Field
Given a quaternion algebra  defined over the field of
rational numbers, return the discriminant of
defined over the field of
rational numbers, return the discriminant of  , i.e. the
product of the ramified primes of
, i.e. the
product of the ramified primes of  .
.
EXAMPLES:
sage: QuaternionAlgebra(210,-22).discriminant()
210
sage: QuaternionAlgebra(19).discriminant()
19
This raises a NotImplementedError if the base field is not the rational numbers:
sage: QuaternionAlgebra(QQ[sqrt(2)],3,19).discriminant()
...
NotImplementedError: base field must be rational numbers
Return the 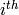 generator of self.
generator of self.
INPUT:
EXAMPLES:
sage: Q.<ii,jj,kk> = QuaternionAlgebra(QQ,-1,-2); Q
Quaternion Algebra (-1, -2) with base ring Rational Field
sage: Q.gen(0)
ii
sage: Q.gen(1)
jj
sage: Q.gen(2)
kk
sage: Q.gens()
[ii, jj, kk]
Return the quaternion ideal with given gens over  .
Neither a left or right order structure need be specified.
.
Neither a left or right order structure need be specified.
INPUT:
EXAMPLES:
sage: R = QuaternionAlgebra(-11,-1)
sage: R.ideal([2*a for a in R.basis()])
Fractional ideal (2, 2*i, 2*j, 2*k)
Return the inner product matrix associated to self, i.e. the
Gram matrix of the reduced norm as a quadratic form on self.
The standard basis  ,
,  ,
,  ,
,  is orthogonal, so this matrix
is just the diagonal matrix with diagonal entries
is orthogonal, so this matrix
is just the diagonal matrix with diagonal entries  ,
,  ,
,  ,
, 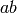 .
.
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(-5,-19)
sage: Q.inner_product_matrix()
[ 2 0 0 0]
[ 0 10 0 0]
[ 0 0 38 0]
[ 0 0 0 190]
sage: R.<a,b> = QQ[]; Q.<i,j,k> = QuaternionAlgebra(Frac(R),a,b)
sage: Q.inner_product_matrix()
[ 2 0 0 0]
[ 0 -2*a 0 0]
[ 0 0 -2*b 0]
[ 0 0 0 2*a*b]
Return the structural invariants  ,
,  of this quaternion
algebra: self is generated by
of this quaternion
algebra: self is generated by  ,
,  subject to
subject to
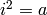 ,
, 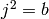 and
and 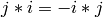 .
.
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(15)
sage: Q.invariants()
(-3, 5)
sage: i^2
-3
sage: j^2
5
Return a maximal order in this quaternion algebra.
OUTPUT: an order in this quaternion algebra
EXAMPLES:
sage: QuaternionAlgebra(-1,-7).maximal_order()
Order of Quaternion Algebra (-1, -7) with base ring Rational Field with basis (1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
Return mod  splitting data for this quaternion algebra at
the unramified prime
splitting data for this quaternion algebra at
the unramified prime  . This is
. This is 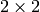 matrices
matrices  ,
, 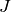 , K over the finite field
, K over the finite field 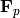 such that if
the quaternion algebra has generators
such that if
the quaternion algebra has generators 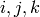 , then
, then 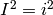 ,
, 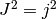 ,
, 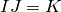 and
and 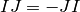 .
.
Note
Currently only implemented when  is odd and the base
ring is
is odd and the base
ring is  .
.
INPUT:
 – unramified odd prime
– unramified odd primeOUTPUT:
EXAMPLES:
sage: Q = QuaternionAlgebra(-15, -19)
sage: Q.modp_splitting_data(7)
(
[0 6] [6 1] [6 6]
[1 0], [1 1], [6 1]
)
sage: Q.modp_splitting_data(next_prime(10^5))
(
[ 0 99988] [97311 4] [99999 59623]
[ 1 0], [13334 2692], [97311 4]
)
sage: I,J,K = Q.modp_splitting_data(23)
sage: I
[0 8]
[1 0]
sage: I^2
[8 0]
[0 8]
sage: J
[19 2]
[17 4]
sage: J^2
[4 0]
[0 4]
sage: I*J == -J*I
True
sage: I*J == K
True
The following is a good test because of the asserts in the code:
sage: v = [Q.modp_splitting_data(p) for p in primes(20,1000)]
Proper error handling:
sage: Q.modp_splitting_data(5)
...
NotImplementedError: algorithm for computing local splittings not implemented in general (currently require the first invariant to be coprime to p)
sage: Q.modp_splitting_data(2)
...
NotImplementedError: p must be odd
Return Python map from the ( -integral) quaternion algebra to
the set of
-integral) quaternion algebra to
the set of 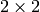 matrices over
matrices over 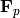 .
.
INPUT:
 – prime number
– prime numberEXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(-1, -7)
sage: f = Q.modp_splitting_map(13)
sage: a = 2+i-j+3*k; b = 7+2*i-4*j+k
sage: f(a*b)
[12 3]
[10 5]
sage: f(a)*f(b)
[12 3]
[10 5]
Return the order of this quaternion order with given basis.
INPUT:
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(-11,-1)
sage: Q.quaternion_order([1,i,j,k])
Order of Quaternion Algebra (-11, -1) with base ring Rational Field with basis (1, i, j, k)
We test out check=False:
sage: Q.quaternion_order([1,i,j,k], check=False)
Order of Quaternion Algebra (-11, -1) with base ring Rational Field with basis [1, i, j, k]
sage: Q.quaternion_order([i,j,k], check=False)
Order of Quaternion Algebra (-11, -1) with base ring Rational Field with basis [i, j, k]
Return the primes that ramify in this quaternion algebra. Currently only implemented over the rational numbers.
EXAMPLES:
sage: QuaternionAlgebra(QQ, -1, -1).ramified_primes()
[2]
Bases: sage.rings.ring.Algebra
Return the fixed basis of self, which is  ,
,  ,
,  ,
,  , where
, where
 ,
,  ,
,  are the generators of self.
are the generators of self.
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(QQ,-5,-2)
sage: Q.basis()
(1, i, j, k)
sage: Q.<xyz,abc,theta> = QuaternionAlgebra(GF(9,'a'),-5,-2)
sage: Q.basis()
(1, xyz, abc, theta)
The basis is cached:
sage: Q.basis() is Q.basis()
True
Return the inner product matrix associated to self, i.e. the
Gram matrix of the reduced norm as a quadratic form on self.
The standard basis  ,
,  ,
,  ,
,  is orthogonal, so this matrix
is just the diagonal matrix with diagonal entries
is orthogonal, so this matrix
is just the diagonal matrix with diagonal entries  ,
, 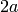 ,
, 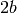 ,
,
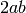 .
.
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(-5,-19)
sage: Q.inner_product_matrix()
[ 2 0 0 0]
[ 0 10 0 0]
[ 0 0 38 0]
[ 0 0 0 190]
Return False always, since all quaternion algebras are noncommutative.
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(QQ, -3,-7)
sage: Q.is_commutative()
False
Return True if the quaternion algebra is a division algebra (i.e. every nonzero element in self is invertible), and False if the quaternion algebra is isomorphic to the 2x2 matrix algebra.
EXAMPLES:
sage: QuaternionAlgebra(QQ,-5,-2).is_division_algebra()
True
sage: QuaternionAlgebra(1).is_division_algebra()
False
sage: QuaternionAlgebra(2,9).is_division_algebra()
False
sage: QuaternionAlgebra(RR(2.),1).is_division_algebra()
...
NotImplementedError: base field must be rational numbers
Return True if elements of this quaternion algebra are represented exactly, i.e. there is no precision loss when doing arithmetic. A quaternion algebra is exact if and only if its base field is exact.
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(QQ, -3, -7)
sage: Q.is_exact()
True
sage: Q.<i,j,k> = QuaternionAlgebra(Qp(7), -3, -7)
sage: Q.is_exact()
False
Return False always, since all quaternion algebras are noncommutative and all fields are commutative.
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(QQ, -3, -7)
sage: Q.is_field()
False
Return True if the quaternion algebra is finite as a set.
Algorithm: A quaternion algebra is finite if and only if the base field is finite.
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(QQ, -3, -7)
sage: Q.is_finite()
False
sage: Q.<i,j,k> = QuaternionAlgebra(GF(5), -3, -7)
sage: Q.is_finite()
True
Return False always, since all quaternion algebras are noncommutative and integral domains are commutative (in Sage).
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(QQ, -3, -7)
sage: Q.is_integral_domain()
False
Return True if the quaternion algebra is isomorphic to the 2x2 matrix ring, and False if self is a division algebra (i.e. every nonzero element in self is invertible).
EXAMPLES:
sage: QuaternionAlgebra(QQ,-5,-2).is_matrix_ring()
False
sage: QuaternionAlgebra(1).is_matrix_ring()
True
sage: QuaternionAlgebra(2,9).is_matrix_ring()
True
sage: QuaternionAlgebra(RR(2.),1).is_matrix_ring()
...
NotImplementedError: base field must be rational numbers
Return True always, since any quaternion algebra is a noetherian ring (because it is a finitely generated module over a field).
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(QQ, -3, -7)
sage: Q.is_noetherian()
True
Return the number of generators of the quaternion algebra as a K-vector
space, not including 1. This value is always 3: the algebra is spanned
by the standard basis  ,
,  ,
,  ,
,  .
.
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(QQ,-5,-2)
sage: Q.ngens()
3
sage: Q.gens()
[i, j, k]
Return the number of elements of the quaternion algebra, or +Infinity if the algebra is not finite.
EXAMPLES:
sage: Q.<i,j,k> = QuaternionAlgebra(QQ, -3, -7)
sage: Q.order()
+Infinity
sage: Q.<i,j,k> = QuaternionAlgebra(GF(5), -3, -7)
sage: Q.order()
625
Return a random element of this quaternion algebra.
The args and kwds are passed to the random_element method of the base ring.
EXAMPLES:
sage: QuaternionAlgebra(QQ[sqrt(2)],-3,7).random_element()
(sqrt2 + 2)*i + (-12*sqrt2 - 2)*j + (-sqrt2 + 1)*k
sage: QuaternionAlgebra(-3,19).random_element()
-1 + 2*i - j - 6/5*k
sage: QuaternionAlgebra(GF(17)(2),3).random_element()
14 + 10*i + 4*j + 7*k
Specify the numerator and denominator bounds:
sage: QuaternionAlgebra(-3,19).random_element(10^6,10^6)
-979933/553629 + 255525/657688*i - 3511/6929*j - 700105/258683*k
Return the vector space associated to self with inner product given by the reduced norm.
EXAMPLES:
sage: QuaternionAlgebra(-3,19).vector_space()
Ambient quadratic space of dimension 4 over Rational Field
Inner product matrix:
[ 2 0 0 0]
[ 0 6 0 0]
[ 0 0 -38 0]
[ 0 0 0 -114]
Bases: sage.algebras.quatalg.quaternion_algebra.QuaternionFractionalIdeal
A fractional ideal in a rational quaternion algebra.
Return basis for this fractional ideal. The basis is in Hermite form.
OUTPUT: tuple
EXAMPLES:
sage: QuaternionAlgebra(-11,-1).maximal_order().unit_ideal().basis()
(1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
Return basis matrix  in Hermite normal form for self as a
matrix with rational entries.
in Hermite normal form for self as a
matrix with rational entries.
If 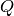 is the ambient quaternion algebra, then the
is the ambient quaternion algebra, then the  -span of
the rows of
-span of
the rows of  viewed as linear combinations of Q.basis() =
viewed as linear combinations of Q.basis() =
![[1,i,j,k]](../../../_images/math/faddecc36af13cb502df97b81717ef3101d2002f.png) is the fractional ideal self. Also, M *
M.denominator() is an integer matrix in Hermite normal form.
is the fractional ideal self. Also, M *
M.denominator() is an integer matrix in Hermite normal form.
OUTPUT: matrix over 
EXAMPLES:
sage: QuaternionAlgebra(-11,-1).maximal_order().unit_ideal().basis_matrix()
[1/2 0 1/2 0]
[ 0 1/2 0 1/2]
[ 0 0 1 0]
[ 0 0 0 1]
Return the ideal with generators the conjugates of the generators for self.
OUTPUT: a quaternionic fractional ideal
EXAMPLES:
sage: I = BrandtModule(3,5).right_ideals()[1]; I
Fractional ideal (2 + 6*j + 4*k, 2*i + 4*j + 34*k, 8*j + 32*k, 40*k)
sage: I.conjugate()
Fractional ideal (2 + 2*j + 28*k, 2*i + 4*j + 34*k, 8*j + 32*k, 40*k)
Let  = self. This function returns the right subideals
= self. This function returns the right subideals
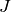 of
of  such that
such that 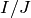 is an
is an 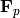 -vector space of
dimension 2.
-vector space of
dimension 2.
INPUT:
– prime number (see below)
– (default: None) element of quaternion algebra, which can be used to parameterize the order of the ideals
. More precisely the
‘s are the right annihilators of
for
OUTPUT:
- list of right ideals
Note
Currently,  must satisfy a bunch of conditions, or a
NotImplementedError is raised. In particular,
must satisfy a bunch of conditions, or a
NotImplementedError is raised. In particular,  must be
odd and unramified in the quaternion algebra, must be
coprime to the index of the right order in the maximal
order, and also coprime to the normal of self. (The Brandt
modules code has a more general algorithm in some cases.)
must be
odd and unramified in the quaternion algebra, must be
coprime to the index of the right order in the maximal
order, and also coprime to the normal of self. (The Brandt
modules code has a more general algorithm in some cases.)
EXAMPLES:
sage: B = BrandtModule(2,37); I = B.right_ideals()[0]
sage: I.cyclic_right_subideals(3)
[Fractional ideal (2 + 2*i + 10*j + 90*k, 4*i + 4*j + 152*k, 12*j + 132*k, 444*k), Fractional ideal (2 + 2*i + 2*j + 150*k, 4*i + 8*j + 196*k, 12*j + 132*k, 444*k), Fractional ideal (2 + 2*i + 6*j + 194*k, 4*i + 8*j + 344*k, 12*j + 132*k, 444*k), Fractional ideal (2 + 2*i + 6*j + 46*k, 4*i + 4*j + 4*k, 12*j + 132*k, 444*k)]
sage: B = BrandtModule(5,389); I = B.right_ideals()[0]
sage: C = I.cyclic_right_subideals(3); C
[Fractional ideal (2 + 10*j + 546*k, i + 6*j + 133*k, 12*j + 3456*k, 4668*k), Fractional ideal (2 + 2*j + 2910*k, i + 6*j + 3245*k, 12*j + 3456*k, 4668*k), Fractional ideal (2 + i + 2295*k, 3*i + 2*j + 3571*k, 4*j + 2708*k, 4668*k), Fractional ideal (2 + 2*i + 2*j + 4388*k, 3*i + 2*j + 2015*k, 4*j + 4264*k, 4668*k)]
sage: [(I.free_module()/J.free_module()).invariants() for J in C]
[(3, 3), (3, 3), (3, 3), (3, 3)]
sage: I.scale(3).cyclic_right_subideals(3)
[Fractional ideal (6 + 30*j + 1638*k, 3*i + 18*j + 399*k, 36*j + 10368*k, 14004*k), Fractional ideal (6 + 6*j + 8730*k, 3*i + 18*j + 9735*k, 36*j + 10368*k, 14004*k), Fractional ideal (6 + 3*i + 6885*k, 9*i + 6*j + 10713*k, 12*j + 8124*k, 14004*k), Fractional ideal (6 + 6*i + 6*j + 13164*k, 9*i + 6*j + 6045*k, 12*j + 12792*k, 14004*k)]
sage: C = I.scale(1/9).cyclic_right_subideals(3); C
[Fractional ideal (2/9 + 10/9*j + 182/3*k, 1/9*i + 2/3*j + 133/9*k, 4/3*j + 384*k, 1556/3*k), Fractional ideal (2/9 + 2/9*j + 970/3*k, 1/9*i + 2/3*j + 3245/9*k, 4/3*j + 384*k, 1556/3*k), Fractional ideal (2/9 + 1/9*i + 255*k, 1/3*i + 2/9*j + 3571/9*k, 4/9*j + 2708/9*k, 1556/3*k), Fractional ideal (2/9 + 2/9*i + 2/9*j + 4388/9*k, 1/3*i + 2/9*j + 2015/9*k, 4/9*j + 4264/9*k, 1556/3*k)]
sage: [(I.scale(1/9).free_module()/J.free_module()).invariants() for J in C]
[(3, 3), (3, 3), (3, 3), (3, 3)]
sage: Q.<i,j,k> = QuaternionAlgebra(-2,-5)
sage: I = Q.ideal([Q(1),i,j,k])
sage: I.cyclic_right_subideals(3)
[Fractional ideal (1 + 2*j, i + k, 3*j, 3*k), Fractional ideal (1 + j, i + 2*k, 3*j, 3*k), Fractional ideal (1 + 2*i, 3*i, j + 2*k, 3*k), Fractional ideal (1 + i, 3*i, j + k, 3*k)]
The general algorithm is not yet implemented here:
sage: I.cyclic_right_subideals(3)[0].cyclic_right_subideals(3)
...
NotImplementedError: general algorithm not implemented (The given basis vectors must be linearly independent.)
Return the underlying free  -module corresponding to this ideal.
-module corresponding to this ideal.
EXAMPLES:
sage: X = BrandtModule(3,5).right_ideals()
sage: X[0]
Fractional ideal (2 + 2*j + 8*k, 2*i + 18*k, 4*j + 16*k, 20*k)
sage: X[0].free_module()
Free module of degree 4 and rank 4 over Integer Ring
Echelon basis matrix:
[ 2 0 2 8]
[ 0 2 0 18]
[ 0 0 4 16]
[ 0 0 0 20]
sage: X[0].scale(1/7).free_module()
Free module of degree 4 and rank 4 over Integer Ring
Echelon basis matrix:
[ 2/7 0 2/7 8/7]
[ 0 2/7 0 18/7]
[ 0 0 4/7 16/7]
[ 0 0 0 20/7]
The free module method is also useful since it allows for checking if one ideal is contained in another, computing quotients I/J, etc.:
sage: X = BrandtModule(3,17).right_ideals()
sage: I = X[0].intersection(X[2]); I
Fractional ideal (2 + 2*j + 164*k, 2*i + 4*j + 46*k, 16*j + 224*k, 272*k)
sage: I.free_module().is_submodule(X[3].free_module())
False
sage: I.free_module().is_submodule(X[1].free_module())
True
sage: X[0].free_module() / I.free_module()
Finitely generated module V/W over Integer Ring with invariants (4, 4)
Return the generators for this ideal, which are the same as
the  -basis for this ideal.
-basis for this ideal.
EXAMPLES:
sage: QuaternionAlgebra(-11,-1).maximal_order().unit_ideal().gens()
(1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
Return the Gram matrix of this fractional ideal.
OUTPUT: 4x4 matrix over  .
.
EXAMPLES:
sage: I = BrandtModule(3,5).right_ideals()[1]; I
Fractional ideal (2 + 6*j + 4*k, 2*i + 4*j + 34*k, 8*j + 32*k, 40*k)
sage: I.gram_matrix()
[ 640 1920 2112 1920]
[ 1920 14080 13440 16320]
[ 2112 13440 13056 15360]
[ 1920 16320 15360 19200]
Return the intersection of the ideals self and 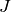 .
.
EXAMPLES:
sage: X = BrandtModule(3,5).right_ideals()
sage: I = X[0].intersection(X[1]); I
Fractional ideal (2 + 6*j + 4*k, 2*i + 4*j + 34*k, 8*j + 32*k, 40*k)
Return True if I and J are equivalent as right ideals.
INPUT:
OUTPUT: bool
EXAMPLES:
sage: R = BrandtModule(3,5).right_ideals(); len(R)
2
sage: R[0].is_equivalent(R[1])
False
sage: R[0].is_equivalent(R[0])
True
sage: OO = R[0].quaternion_order()
sage: S = OO.right_ideal([3*a for a in R[0].basis()])
sage: R[0].is_equivalent(S)
True
Return the left order associated to this fractional ideal.
OUTPUT: an order in a quaternion algebra
EXAMPLES:
sage: B = BrandtModule(11)
sage: R = B.maximal_order()
sage: I = R.unit_ideal()
sage: I.left_order()
Order of Quaternion Algebra (-1, -11) with base ring Rational Field with basis (1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
We do a consistency check:
sage: B = BrandtModule(11,19); R = B.right_ideals()
sage: print [r.left_order().discriminant() for r in R]
[209, 209, 209, 209, 209, 209, 209, 209, 209, 209, 209, 209, 209, 209, 209, 209, 209, 209]
Return product of self and the conjugate Jbar of 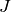 .
.
INPUT:
OUTPUT: a quaternionic fractional ideal.
EXAMPLES:
sage: R = BrandtModule(3,5).right_ideals()
sage: R[0].multiply_by_conjugate(R[1])
Fractional ideal (8 + 8*j + 112*k, 8*i + 16*j + 136*k, 32*j + 128*k, 160*k)
sage: R[0]*R[1].conjugate()
Fractional ideal (8 + 8*j + 112*k, 8*i + 16*j + 136*k, 32*j + 128*k, 160*k)
Return the norm of this fractional ideal.
OUTPUT: rational number
EXAMPLES:
sage: C = BrandtModule(37).right_ideals()
sage: [I.norm() for I in C]
[32, 64, 64]
Return the normalized quadratic form associated to this quaternion ideal.
OUTPUT: quadratic form
EXAMPLES:
sage: I = BrandtModule(11).right_ideals()[1]
sage: Q = I.quadratic_form(); Q
Quadratic form in 4 variables over Rational Field with coefficients:
[ 18 22 33 22 ]
[ * 7 22 11 ]
[ * * 22 0 ]
[ * * * 22 ]
sage: Q.theta_series(10)
1 + 12*q^2 + 12*q^3 + 12*q^4 + 12*q^5 + 24*q^6 + 24*q^7 + 36*q^8 + 36*q^9 + O(q^10)
sage: I.theta_series(10)
1 + 12*q^2 + 12*q^3 + 12*q^4 + 12*q^5 + 24*q^6 + 24*q^7 + 36*q^8 + 36*q^9 + O(q^10)
Return the ambient quaternion algebra that contains this fractional ideal.
OUTPUT: a quaternion algebra
EXAMPLES:
sage: I = BrandtModule(3,5).right_ideals()[1]; I
Fractional ideal (2 + 6*j + 4*k, 2*i + 4*j + 34*k, 8*j + 32*k, 40*k)
sage: I.quaternion_algebra()
Quaternion Algebra (-1, -3) with base ring Rational Field
Return the order for which this ideal is a left or right fractional ideal. If this ideal has both a left and right ideal structure, then the left order is returned. If it has neither structure, then an error is raised.
OUTPUT: QuaternionOrder
EXAMPLES:
sage: R = QuaternionAlgebra(-11,-1).maximal_order()
sage: R.unit_ideal().quaternion_order() is R
True
Return the right order associated to this fractional ideal.
OUTPUT: an order in a quaternion algebra
EXAMPLES:
sage: I = BrandtModule(389).right_ideals()[1]; I
Fractional ideal (2 + 6*j + 2*k, i + 2*j + k, 8*j, 8*k)
sage: I.right_order()
Order of Quaternion Algebra (-2, -389) with base ring Rational Field with basis (1/2 + 1/2*j + 1/2*k, 1/4*i + 1/2*j + 1/4*k, j, k)
sage: I.left_order()
Order of Quaternion Algebra (-2, -389) with base ring Rational Field with basis (1/2 + 1/2*j + 3/2*k, 1/8*i + 1/4*j + 9/8*k, j + k, 2*k)
The following is a big consistency check. We take reps for all the right ideal classes of a certain order, take the corresponding left orders, then take ideals in the left orders and from those compute the right order again:
sage: B = BrandtModule(11,19); R = B.right_ideals()
sage: O = [r.left_order() for r in R]
sage: J = [O[i].left_ideal(R[i].basis()) for i in range(len(R))]
sage: len(set(J))
18
sage: len(set([I.right_order() for I in J]))
1
sage: J[0].right_order() == B.order_of_level_N()
True
Return ring that this is a fractional ideal for.
EXAMPLES:
sage: R = QuaternionAlgebra(-11,-1).maximal_order()
sage: R.unit_ideal().ring() is R
True
Scale the fractional ideal self by multiplying the basis by alpha.
INPUT:
– element of quaternion algebra
- left – bool (default: False); if true multiply
on the left, otherwise multiply
on the right.
OUTPUT:
- a new fractional ideal
EXAMPLES:
sage: B = BrandtModule(5,37); I = B.right_ideals()[0]; i,j,k = B.quaternion_algebra().gens(); I
Fractional ideal (2 + 2*j + 106*k, i + 2*j + 105*k, 4*j + 64*k, 148*k)
sage: I.scale(i)
Fractional ideal [2*i + 212*j - 2*k, -2 + 210*j - 2*k, 128*j - 4*k, 296*j]
sage: I.scale(i, left=True)
Fractional ideal [2*i - 212*j + 2*k, -2 - 210*j + 2*k, -128*j + 4*k, -296*j]
sage: I.scale(i, left=False)
Fractional ideal [2*i + 212*j - 2*k, -2 + 210*j - 2*k, 128*j - 4*k, 296*j]
sage: i * I.gens()[0]
2*i - 212*j + 2*k
sage: I.gens()[0] * i
2*i + 212*j - 2*k
Return normalized theta series of self, as a power series over
 in the variable var, which is ‘q’ by default.
in the variable var, which is ‘q’ by default.
The normalized theta series is by definition
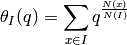
INPUT:
OUTPUT: power series
EXAMPLES:
sage: I = BrandtModule(11).right_ideals()[1]; I
Fractional ideal (2 + 6*j + 4*k, 2*i + 4*j + 2*k, 8*j, 8*k)
sage: I.norm()
64
sage: I.theta_series(5)
1 + 12*q^2 + 12*q^3 + 12*q^4 + O(q^5)
sage: I.theta_series(5,'T')
1 + 12*T^2 + 12*T^3 + 12*T^4 + O(T^5)
sage: I.theta_series(3)
1 + 12*q^2 + O(q^3)
Return theta series coefficients of self, as a vector of  integers.
integers.
INPUT:
OUTPUT: vector over  with B entries
with B entries
EXAMPLES:
sage: I = BrandtModule(37).right_ideals()[1]; I
Fractional ideal (2 + 6*j + 2*k, i + 2*j + k, 8*j, 8*k)
sage: I.theta_series_vector(5)
(1, 0, 2, 2, 6)
sage: I.theta_series_vector(10)
(1, 0, 2, 2, 6, 4, 8, 6, 10, 10)
sage: I.theta_series_vector(5)
(1, 0, 2, 2, 6)
Bases: sage.rings.ring.Algebra
An order in a quaternion algebra.
EXAMPLES:
sage: QuaternionAlgebra(-1,-7).maximal_order()
Order of Quaternion Algebra (-1, -7) with base ring Rational Field with basis (1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
sage: type(QuaternionAlgebra(-1,-7).maximal_order())
<class 'sage.algebras.quatalg.quaternion_algebra.QuaternionOrder'>
Return fix choice of basis for this quaternion order.
EXAMPLES:
sage: QuaternionAlgebra(-11,-1).maximal_order().basis()
(1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
Return the discriminant of this order, which we define as
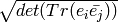 , where
, where 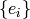 is the
basis of the order.
is the
basis of the order.
OUTPUT: rational number
EXAMPLES:
sage: QuaternionAlgebra(-11,-1).maximal_order().discriminant()
11
sage: S = BrandtModule(11,5).order_of_level_N()
sage: S.discriminant()
55
sage: type(S.discriminant())
<type 'sage.rings.rational.Rational'>
Return the free  -module that corresponds to this order
inside the vector space corresponding to the ambient
quaternion algebra.
-module that corresponds to this order
inside the vector space corresponding to the ambient
quaternion algebra.
OUTPUT: a free  -module of rank 4
-module of rank 4
EXAMPLES:
sage: R = QuaternionAlgebra(-11,-1).maximal_order()
sage: R.basis()
(1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
sage: R.free_module()
Free module of degree 4 and rank 4 over Integer Ring
Echelon basis matrix:
[1/2 0 1/2 0]
[ 0 1/2 0 1/2]
[ 0 0 1 0]
[ 0 0 0 1]
Return the n-th generator.
INPUT:
EXAMPLES:
sage: R = QuaternionAlgebra(-11,-1).maximal_order(); R
Order of Quaternion Algebra (-11, -1) with base ring Rational Field with basis (1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
sage: R.gen(0)
1/2 + 1/2*j
sage: R.gen(1)
1/2*i + 1/2*k
sage: R.gen(2)
j
sage: R.gen(3)
k
Return generators for self.
EXAMPLES:
sage: QuaternionAlgebra(-1,-7).maximal_order().gens()
(1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
Return the intersection of this order with other.
INPUT:
OUTPUT: a quaternion order
EXAMPLES:
sage: R = QuaternionAlgebra(-11,-1).maximal_order()
sage: R.intersection(R)
Order of Quaternion Algebra (-11, -1) with base ring Rational Field with basis (1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
We intersect various orders in the quaternion algebra ramified at 11:
sage: B = BrandtModule(11,3)
sage: R = B.maximal_order(); S = B.order_of_level_N()
sage: R.intersection(S)
Order of Quaternion Algebra (-1, -11) with base ring Rational Field with basis (1/2 + 1/2*j, 1/2*i + 5/2*k, j, 3*k)
sage: R.intersection(S) == S
True
sage: B = BrandtModule(11,5)
sage: T = B.order_of_level_N()
sage: S.intersection(T)
Order of Quaternion Algebra (-1, -11) with base ring Rational Field with basis (1/2 + 1/2*j, 1/2*i + 23/2*k, j, 15*k)
Return the ideal with given gens over  .
.
INPUT:
EXAMPLES:
sage: R = QuaternionAlgebra(-11,-1).maximal_order()
sage: R.left_ideal([2*a for a in R.basis()])
Fractional ideal (1 + j, i + k, 2*j, 2*k)
Return the number of generators (which is 4).
EXAMPLES:
sage: QuaternionAlgebra(-1,-7).maximal_order().ngens()
4
Return the normalized quadratic form associated to this quaternion order.
OUTPUT: quadratic form
EXAMPLES:
sage: R = BrandtModule(11,13).order_of_level_N()
sage: Q = R.quadratic_form(); Q
Quadratic form in 4 variables over Rational Field with coefficients:
[ 14 253 55 286 ]
[ * 1455 506 3289 ]
[ * * 55 572 ]
[ * * * 1859 ]
sage: Q.theta_series(10)
1 + 2*q + 2*q^4 + 4*q^6 + 4*q^8 + 2*q^9 + O(q^10)
Return ambient quaternion algebra that contains this quaternion order.
EXAMPLES:
sage: QuaternionAlgebra(-11,-1).maximal_order().quaternion_algebra()
Quaternion Algebra (-11, -1) with base ring Rational Field
Return a random element of this order.
The args and kwds are passed to the random_element method of the integer ring, and we return an element of the form
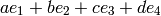
where 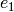 , ...,
, ..., 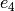 are the basis of this order and
are the basis of this order and  ,
,
 ,
,  ,
,  are random integers.
are random integers.
EXAMPLES:
sage: QuaternionAlgebra(-11,-1).maximal_order().random_element()
-4 + i - 4*j + k
sage: QuaternionAlgebra(-11,-1).maximal_order().random_element(-10,10)
-9/2 - 7/2*i - 7/2*j + 3/2*k
Return the ideal with given gens over  .
.
INPUT:
EXAMPLES:
sage: R = QuaternionAlgebra(-11,-1).maximal_order()
sage: R.right_ideal([2*a for a in R.basis()])
Fractional ideal (1 + j, i + k, 2*j, 2*k)
Return the ternary quadratic form associated to this order.
INPUT:

OUTPUT:
This function computes the positive definition quadratic form
obtained by letting G be the trace zero subspace of  +
2* self, which has rank 3, and restricting the pairing
+
2* self, which has rank 3, and restricting the pairing
(x,y) = (x.conjugate()*y).reduced_trace()
to  .
.
APPLICATIONS: Ternary quadratic forms associated to an order in a rational quaternion algebra are useful in computing with Gross points, in decided whether quaternion orders have embeddings from orders in quadratic imaginary fields, and in computing elements of the Kohnen plus subspace of modular forms of weight 3/2.
EXAMPLES:
sage: R = BrandtModule(11,13).order_of_level_N()
sage: Q = R.ternary_quadratic_form(); Q
Quadratic form in 3 variables over Rational Field with coefficients:
[ 5820 1012 13156 ]
[ * 55 1144 ]
[ * * 7436 ]
sage: factor(Q.disc())
2^4 * 11^2 * 13^2
The following theta series is a modular form of weight 3/2 and level 4*11*13:
sage: Q.theta_series(100)
1 + 2*q^23 + 2*q^55 + 2*q^56 + 2*q^75 + 4*q^92 + O(q^100)
Return the unit ideal in this quaternion order.
EXAMPLES:
sage: R = QuaternionAlgebra(-11,-1).maximal_order()
sage: I = R.unit_ideal(); I
Fractional ideal (1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
Return a basis for the  -lattice in a quaternion algebra
spanned by the given gens.
-lattice in a quaternion algebra
spanned by the given gens.
INPUT:
EXAMPLES:
sage: A.<i,j,k> = QuaternionAlgebra(-1,-7)
sage: sage.algebras.quatalg.quaternion_algebra.basis_for_quaternion_lattice([i+j, i-j, 2*k, A(1/3)])
[1/3, i + j, 2*j, 2*k]
Intersects the  -modules with basis matrices the full rank 4x4
-modules with basis matrices the full rank 4x4
 -matrices in the list v. The returned intersection is
represented by a 4x4 matrix over
-matrices in the list v. The returned intersection is
represented by a 4x4 matrix over  . This can also be done using
modules and intersection, but that would take over twice as long
because of overhead, hence this function.
. This can also be done using
modules and intersection, but that would take over twice as long
because of overhead, hence this function.
EXAMPLES:
sage: a = matrix(QQ,4,[-2, 0, 0, 0, 0, -1, -1, 1, 2, -1/2, 0, 0, 1, 1, -1, 0])
sage: b = matrix(QQ,4,[0, -1/2, 0, -1/2, 2, 1/2, -1, -1/2, 1, 2, 1, -2, 0, -1/2, -2, 0])
sage: c = matrix(QQ,4,[0, 1, 0, -1/2, 0, 0, 2, 2, 0, -1/2, 1/2, -1, 1, -1, -1/2, 0])
sage: v = [a,b,c]
sage: from sage.algebras.quatalg.quaternion_algebra import intersection_of_row_modules_over_ZZ
sage: M = intersection_of_row_modules_over_ZZ(v); M
[ 2 0 -1 -1]
[ 4 -1 -1 3]
[ -3 19/2 -1 -4]
[ 2 -3 -8 4]
sage: M2 = a.row_module(ZZ).intersection(b.row_module(ZZ)).intersection(c.row_module(ZZ))
sage: M.row_module(ZZ) == M2
True
Return True if A is of the QuaternionAlgebra data type.
EXAMPLES:
sage: sage.algebras.quatalg.quaternion_algebra.is_QuaternionAlgebra(QuaternionAlgebra(QQ,-1,-1))
True
sage: sage.algebras.quatalg.quaternion_algebra.is_QuaternionAlgebra(ZZ)
False
The 0th version of pickling for quaternion algebras.
EXAMPLES:
sage: Q = QuaternionAlgebra(-5,-19)
sage: f, t = Q.__reduce__()
sage: sage.algebras.quatalg.quaternion_algebra.unpickle_QuaternionAlgebra_v0(*t)
Quaternion Algebra (-5, -19) with base ring Rational Field
sage: loads(dumps(Q)) == Q
True
sage: loads(dumps(Q)) is Q
True