Elements of Quaternion Algebras¶

Sage allows for computation with elements of quaternion algebras over a nearly arbitrary base field of characteristic not 2. Sage also has very highly optimized implementation of arithmetic in rational quaternion algebras and quaternion algebras over number fields.

class sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_abstract¶

Bases: sage.structure.element.AlgebraElement

coefficient_tuple()¶

Return 4-tuple of coefficients of this quaternion.

EXAMPLES:

sage: K.<x> = QQ['x']
sage: Q.<i,j,k> = QuaternionAlgebra(Frac(K),-5,-2)
sage: a = 1/2*x^2 + 2/3*x*i - 3/4*j + 5/7*k
sage: type(a)
<type 'sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_generic'>
sage: a.coefficient_tuple()
(1/2*x^2, 2/3*x, -3/4, 5/7)

conjugate()¶

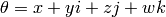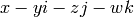Return the conjugate of the quaternion: if $\theta = x + yi + zj + wk$ , return $x - yi - zj - wk$ ; that is, return theta.reduced_trace() - theta.

EXAMPLES:

sage: A.<i,j,k> = QuaternionAlgebra(QQ,-5,-2)
sage: a = 3*i - j + 2
sage: type(a)
<type 'sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_rational_field'>
sage: a.conjugate()
2 - 3*i + j

The “universal” test:

sage: K.<x,y,z,w,a,b> = QQ[]
sage: Q.<i,j,k> = QuaternionAlgebra(a,b)
sage: theta = x+y*i+z*j+w*k
sage: theta.conjugate()
x + (-y)*i + (-z)*j + (-w)*k

is_constant()¶

Return True if this quaternion is constant, i.e., has no i, j, or k term.

OUTPUT:: bool

EXAMPLES:

sage: A.<i,j,k>=QuaternionAlgebra(-1,-2)
sage: A(1).is_constant()
True
sage: A(1+i).is_constant()
False
sage: A(i).is_constant()
False

matrix(action='right')¶

Return the matrix of right or left multiplication of self on the basis for the ambient quaternion algebra. In particular, if action is ‘right’ (the default), returns the matrix of the mapping sending x to x*self.

INPUT:

action – (default: ‘right’) ‘right’ or ‘left’.

OUTPUT:

a matrix

EXAMPLES:

sage: Q.<i,j,k> = QuaternionAlgebra(-3,-19)
sage: a = 2/3 -1/2*i + 3/5*j - 4/3*k
sage: a.matrix()
[  2/3  -1/2   3/5  -4/3]
[  3/2   2/3     4   3/5]
[-57/5 -76/3   2/3   1/2]
[   76 -57/5  -3/2   2/3]
sage: a.matrix() == a.matrix(action='right')
True
sage: a.matrix(action='left')
[  2/3  -1/2   3/5  -4/3]
[  3/2   2/3    -4  -3/5]
[-57/5  76/3   2/3  -1/2]
[   76  57/5   3/2   2/3]
sage: (i*a,j*a,k*a)
(3/2 + 2/3*i + 4*j + 3/5*k, -57/5 - 76/3*i + 2/3*j + 1/2*k, 76 - 57/5*i - 3/2*j + 2/3*k)
sage: a.matrix(action='foo')
...
ValueError: action must be either 'left' or 'right'

We test over a more generic base field:

sage: K.<x> = QQ[‘x’] sage: Q.<i,j,k> = QuaternionAlgebra(Frac(K),-5,-2) sage: a = 1/2*x^2 + 2/3*x*i - 3/4*j + 5/7*k sage: type(a) <type ‘sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_generic’> sage: a.matrix() [1/2*x^2 2/3*x -3/4 5/7] [-10/3*x 1/2*x^2 -25/7 -3/4] [ 3/2 10/7 1/2*x^2 -2/3*x] [ -50/7 3/2 10/3*x 1/2*x^2]

pair(right)¶

Return the result of pairing self and right, which should both be elements of a quaternion algebra. The pairing is (x,y) = (x.conjugate()*y).reduced_trace().

INPUT:

right – quaternion

EXAMPLES:

sage: A.<i,j,k>=QuaternionAlgebra(-1,-2)
sage: (1+i+j-2*k).pair(2/3+5*i-3*j+k)
-26/3
sage: x = 1+i+j-2*k; y = 2/3+5*i-3*j+k
sage: x.pair(y)
-26/3
sage: y.pair(x)
-26/3
sage: (x.conjugate()*y).reduced_trace()
-26/3

reduced_characteristic_polynomial(var='x')¶

Return the reduced characteristic polynomial of this quaternion algebra element, which is 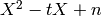$X^2 - tX + n$ , where $t$ is the reduced trace and $n$ is the reduced norm.

INPUT:

var – string (default: ‘x’); indeterminate of characteristic polynomial

EXAMPLES:

sage: A.<i,j,k>=QuaternionAlgebra(-1,-2)
sage: i.reduced_characteristic_polynomial()
x^2 + 1
sage: j.reduced_characteristic_polynomial()
x^2 + 2
sage: (i+j).reduced_characteristic_polynomial()
x^2 + 3
sage: (2+j+k).reduced_trace()
4
sage: (2+j+k).reduced_characteristic_polynomial('T')
T^2 - 4*T + 8

reduced_norm()¶

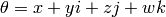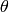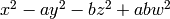Return the reduced norm of self: if $\theta = x + yi + zj + wk$ , then $\theta$ has reduced norm $x^2 - ay^2 - bz^2 + abw^2$ .

EXAMPLES:

sage: K.<x,y,z,w,a,b> = QQ[]
sage: Q.<i,j,k> = QuaternionAlgebra(a,b)
sage: theta = x+y*i+z*j+w*k
sage: theta.reduced_norm()
w^2*a*b - y^2*a - z^2*b + x^2

reduced_trace()¶

Return the reduced trace of self: if 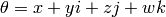$\the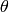ta = x + yi + zj + wk$ , then $\theta$ has reduced trace $2x$ .

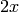EXAMPLES:

sage: K.<x,y,z,w,a,b> = QQ[]
sage: Q.<i,j,k> = QuaternionAlgebra(a,b)
sage: theta = x+y*i+z*j+w*k
sage: theta.reduced_trace()
2*x

class sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_generic¶

Bases: sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_abstract

TESTS:

We test pickling:

sage: R.<x> = Frac(QQ['x']); Q.<i,j,k> = QuaternionAlgebra(R,-5*x,-2)
sage: theta = x + i*x^3 + j*x^2 + k*x
sage: theta == loads(dumps(theta))
True

class sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_number_field¶: Bases: sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_abstract

class sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_rational_field¶

Bases: sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_abstract

TESTS:

We test pickling:

sage: Q.<i,j,k> = QuaternionAlgebra(QQ,-5,-2)
sage: i + j + k == loads(dumps(i+j+k))
True

coefficient_tuple()¶

Return 4-tuple of rational numbers which are the coefficients of this quaternion.

EXAMPLES:

sage: A.<i,j,k>=QuaternionAlgebra(-1,-2)
sage: (2/3 + 3/5*i + 4/3*j - 5/7*k).coefficient_tuple()
(2/3, 3/5, 4/3, -5/7)

conjugate()¶

Return the conjugate of this quaternion.

EXAMPLES:

sage: A.<i,j,k> = QuaternionAlgebra(QQ,-5,-2)
sage: a = 3*i - j + 2
sage: type(a)
<type 'sage.algebras.quatalg.quaternion_algebra_element.QuaternionAlgebraElement_rational_field'>
sage: a.conjugate()
2 - 3*i + j
sage: b = 1 + 1/3*i + 1/5*j - 1/7*k
sage: b.conjugate()
1 - 1/3*i - 1/5*j + 1/7*k

denominator()¶

Return the lowest common multiple of the denominators of the coefficients of i, j and k for this quaternion.

EXAMPLES:

sage: A = QuaternionAlgebra(QQ, -1, -1)
sage: A.<i,j,k> = QuaternionAlgebra(QQ, -1, -1)
sage: a = (1/2) + (1/5)*i + (5/12)*j + (1/13)*k
sage: a
1/2 + 1/5*i + 5/12*j + 1/13*k
sage: a.denominator()
780
sage: lcm([2, 5, 12, 13])
780
sage: (a * a).denominator()
608400
sage: (a + a).denominator()
390

denominator_and_integer_coefficient_tuple()¶

Return 5-tuple d, x, y, z, w, where this rational quaternion is equal to 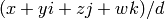$(x + yi + zj + wk)/d$ and x, y, z, w do not share a common factor with d.

OUTPUT:: 5-tuple of Integers

EXAMPLES:

sage: A.<i,j,k>=QuaternionAlgebra(-1,-2)
sage: (2 + 3*i + 4/3*j - 5*k).denominator_and_integer_coefficient_tuple()
(3, 6, 9, 4, -15)

integer_coefficient_tuple()¶

Returns integer part of this quaternion, ignoring the common denominator.

OUTPUT:: 4-tuple of Integers

EXAMPLES:

sage: A.<i,j,k>=QuaternionAlgebra(-1,-2)
sage: (2 + 3*i + 4/3*j - 5*k).integer_coefficient_tuple()
(6, 9, 4, -15)

is_constant()¶

Return True if this quaternion is constant, i.e., has no i, j, or k term.

OUTPUT:: bool

EXAMPLES:

sage: A.<i,j,k>=QuaternionAlgebra(-1,-2)
sage: A(1/3).is_constant()
True
sage: A(-1).is_constant()
True
sage: (1+i).is_constant()
False
sage: j.is_constant()
False

reduced_norm()¶

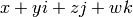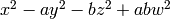Return the reduced norm of self. Given a quaternion $x+yi+zj+wk$ , this is $x^2 - ay^2 - bz^2 + abw^2$ .

EXAMPLES:

sage: K.<i,j,k> = QuaternionAlgebra(QQ, -5, -2)
sage: i.reduced_norm()
5
sage: j.reduced_norm()
2
sage: a = 1/3 + 1/5*i + 1/7*j + k
sage: a.reduced_norm()
22826/2205

reduced_trace()¶

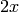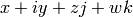Return the reduced trace of self, which is $2x$ if self is $x+iy+zj+wk$ .

EXAMPLES:

sage: K.<i,j,k> = QuaternionAlgebra(QQ, -5, -2)
sage: i.reduced_trace()
0
sage: j.reduced_trace()
0
sage: a = 1/3 + 1/5*i + 1/7*j + k
sage: a.reduced_trace()
2/3

sage.algebras.quatalg.quaternion_algebra_element.clear_mpz_globals()¶

sage.algebras.quatalg.quaternion_algebra_element.gmp_randrange(n1, n2)¶

sage.algebras.quatalg.quaternion_algebra_element.init_mpz_globals()¶

sage.algebras.quatalg.quaternion_algebra_element.unpickle_QuaternionAlgebraElement_generic_v0(*args)¶

EXAMPLES:

sage: K.<X> = QQ[]
sage: Q.<i,j,k> = QuaternionAlgebra(Frac(K), -5,-19); z = 2/3 + i*X - X^2*j + X^3*k
sage: f, t = z.__reduce__()
sage: sage.algebras.quatalg.quaternion_algebra_element.unpickle_QuaternionAlgebraElement_generic_v0(*t)
2/3 + X*i + (-X^2)*j + X^3*k
sage: sage.algebras.quatalg.quaternion_algebra_element.unpickle_QuaternionAlgebraElement_generic_v0(*t) == z
True

sage.algebras.quatalg.quaternion_algebra_element.unpickle_QuaternionAlgebraElement_number_field_v0(*args)¶

EXAMPLES:

sage: K.<a> = QQ[2^(1/3)]; Q.<i,j,k> = QuaternionAlgebra(K, -3, a); z = i + j
sage: f, t = z.__reduce__()
sage: sage.algebras.quatalg.quaternion_algebra_element.unpickle_QuaternionAlgebraElement_number_field_v0(*t)
i + j
sage: sage.algebras.quatalg.quaternion_algebra_element.unpickle_QuaternionAlgebraElement_number_field_v0(*t) == z
True

sage.algebras.quatalg.quaternion_algebra_element.unpickle_QuaternionAlgebraElement_rational_field_v0(*args)¶

EXAMPLES:

sage: Q.<i,j,k> = QuaternionAlgebra(-5,-19); a = 2/3 + i*5/7 - j*2/5 +19/2
sage: f, t = a.__reduce__()
sage: sage.algebras.quatalg.quaternion_algebra_element.unpickle_QuaternionAlgebraElement_rational_field_v0(*t)
61/6 + 5/7*i - 2/5*j

Elements of Quaternion Algebras¶

Previous topic

Next topic

This Page

Navigation

Elements of Quaternion Algebras¶

Previous topic

Next topic

This Page

Quick search

Navigation