The symbolic ring

class sage.symbolic.ring.NumpyToSRMorphism

Bases: sage.categories.morphism.Morphism

class sage.symbolic.ring.SymbolicRing

Bases: sage.rings.ring.CommutativeRing

Symbolic Ring, parent object for all symbolic expressions.

characteristic()

Return the characteristic of the symbolic ring, which is 0.

OUTPUT:

• a Sage integer

EXAMPLES:

sage: c = SR.characteristic(); c
0
sage: type(c)
<type 'sage.rings.integer.Integer'>

is_exact()

Return False, because there are approximate elements in the symbolic ring.

EXAMPLES:

sage: SR.is_exact()
False

Here is an inexact element.

sage: SR(1.9393)
1.93930000000000

is_field(proof=True)

Returns True, since the symbolic expression ring is (for the most part) a field.

EXAMPLES:

sage: SR.is_field()
True

pi()

EXAMPLES:

sage: SR.pi() is pi
True

symbol(name=None, latex_name=None, domain=None)

EXAMPLES:

sage: t0 = SR.symbol("t0")
sage: t0.conjugate()
conjugate(t0)

sage: t1 = SR.symbol("t1", domain='real')
sage: t1.conjugate()
t1

sage: t0.abs()
abs(t0)

sage: t0_2 = SR.symbol("t0", domain='positive')
sage: t0_2.abs()
t0
sage: bool(t0_2 == t0)
True
sage: t0.conjugate()
t0

sage: SR.symbol() # temporary variable
symbol...

var(name, latex_name=None, domain=None)

Return the symbolic variable defined by x as an element of the symbolic ring.

EXAMPLES:

sage: zz = SR.var('zz'); zz
zz
sage: type(zz)
<type 'sage.symbolic.expression.Expression'>
sage: t = SR.var('theta2'); t
theta2

wild(n=0)

Return the n-th wild-card for pattern matching and substitution.

INPUT:

• n - a nonnegative integer

OUTPUT:

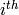• wildcard expression

EXAMPLES:

sage: x,y = var('x,y')
sage: w0 = SR.wild(0); w1 = SR.wild(1)
sage: pattern = sin(x)*w0*w1^2; pattern
$0*$1^2*sin(x)
sage: f = atan(sin(x)*3*x^2); f
arctan(3*x^2*sin(x))
sage: f.has(pattern)
True
sage: f.subs(pattern == x^2)
arctan(x^2)

class sage.symbolic.ring.UnderscoreSageMorphism

Bases: sage.categories.morphism.Morphism

sage.symbolic.ring.is_SymbolicExpressionRing(R)

Returns True if R is the symbolic expression ring.

EXAMPLES:

sage: from sage.symbolic.ring import is_SymbolicExpressionRing
sage: is_SymbolicExpressionRing(ZZ)
False
sage: is_SymbolicExpressionRing(SR)
True

sage.symbolic.ring.is_SymbolicVariable(x)

Returns True if x is a variable.

EXAMPLES:

sage: from sage.symbolic.ring import is_SymbolicVariable
sage: is_SymbolicVariable(x)
True
sage: is_SymbolicVariable(x+2)
False

TESTS:

sage: ZZ[x]
Univariate Polynomial Ring in x over Integer Ring

sage.symbolic.ring.the_SymbolicRing()

Return the unique symbolic ring object.

(This is mainly used for unpickling.)

EXAMPLES:

sage: sage.symbolic.ring.the_SymbolicRing()
Symbolic Ring
sage: sage.symbolic.ring.the_SymbolicRing() is sage.symbolic.ring.the_SymbolicRing()
True
sage: sage.symbolic.ring.the_SymbolicRing() is SR
True

sage.symbolic.ring.var(name, **kwds)

EXAMPLES:

sage: from sage.symbolic.ring import var
sage: var("x y z")
(x, y, z)
sage: var("x,y,z")
(x, y, z)
sage: var("x , y , z")
(x, y, z)
sage: var("z")
z