EXAMPLES: We illustrate each of the calculus functional functions.
sage: simplify(x - x)
0
sage: a = var('a')
sage: derivative(x^a + sin(x), x)
a*x^(a - 1) + cos(x)
sage: diff(x^a + sin(x), x)
a*x^(a - 1) + cos(x)
sage: derivative(x^a + sin(x), x)
a*x^(a - 1) + cos(x)
sage: integral(a*x*sin(x), x)
-(x*cos(x) - sin(x))*a
sage: integrate(a*x*sin(x), x)
-(x*cos(x) - sin(x))*a
sage: limit(a*sin(x)/x, x=0)
a
sage: taylor(a*sin(x)/x, x, 0, 4)
1/120*a*x^4 - 1/6*a*x^2 + a
sage: expand( (x-a)^3 )
-a^3 + 3*a^2*x - 3*a*x^2 + x^3
sage: laplace( e^(x+a), x, a)
e^a/(a - 1)
sage: inverse_laplace( e^a/(a-1), x, a)
ilt(e^a/(a - 1), x, a)
The derivative of  .
.
Repeated differentiation is supported by the syntax given in the examples below.
ALIAS: diff
EXAMPLES: We differentiate a callable symbolic function:
sage: f(x,y) = x*y + sin(x^2) + e^(-x)
sage: f
(x, y) |--> x*y + e^(-x) + sin(x^2)
sage: derivative(f, x)
(x, y) |--> 2*x*cos(x^2) + y - e^(-x)
sage: derivative(f, y)
(x, y) |--> x
We differentiate a polynomial:
sage: t = polygen(QQ, 't')
sage: f = (1-t)^5; f
-t^5 + 5*t^4 - 10*t^3 + 10*t^2 - 5*t + 1
sage: derivative(f)
-5*t^4 + 20*t^3 - 30*t^2 + 20*t - 5
sage: derivative(f, t)
-5*t^4 + 20*t^3 - 30*t^2 + 20*t - 5
sage: derivative(f, t, t)
-20*t^3 + 60*t^2 - 60*t + 20
sage: derivative(f, t, 2)
-20*t^3 + 60*t^2 - 60*t + 20
sage: derivative(f, 2)
-20*t^3 + 60*t^2 - 60*t + 20
We differentiate a symbolic expression:
sage: var('a x')
(a, x)
sage: f = exp(sin(a - x^2))/x
sage: derivative(f, x)
-2*e^(sin(-x^2 + a))*cos(-x^2 + a) - e^(sin(-x^2 + a))/x^2
sage: derivative(f, a)
e^(sin(-x^2 + a))*cos(-x^2 + a)/x
Syntax for repeated differentiation:
sage: R.<u, v> = PolynomialRing(QQ)
sage: f = u^4*v^5
sage: derivative(f, u)
4*u^3*v^5
sage: f.derivative(u) # can always use method notation too
4*u^3*v^5
sage: derivative(f, u, u)
12*u^2*v^5
sage: derivative(f, u, u, u)
24*u*v^5
sage: derivative(f, u, 3)
24*u*v^5
sage: derivative(f, u, v)
20*u^3*v^4
sage: derivative(f, u, 2, v)
60*u^2*v^4
sage: derivative(f, u, v, 2)
80*u^3*v^3
sage: derivative(f, [u, v, v])
80*u^3*v^3
The derivative of  .
.
Repeated differentiation is supported by the syntax given in the examples below.
ALIAS: diff
EXAMPLES: We differentiate a callable symbolic function:
sage: f(x,y) = x*y + sin(x^2) + e^(-x)
sage: f
(x, y) |--> x*y + e^(-x) + sin(x^2)
sage: derivative(f, x)
(x, y) |--> 2*x*cos(x^2) + y - e^(-x)
sage: derivative(f, y)
(x, y) |--> x
We differentiate a polynomial:
sage: t = polygen(QQ, 't')
sage: f = (1-t)^5; f
-t^5 + 5*t^4 - 10*t^3 + 10*t^2 - 5*t + 1
sage: derivative(f)
-5*t^4 + 20*t^3 - 30*t^2 + 20*t - 5
sage: derivative(f, t)
-5*t^4 + 20*t^3 - 30*t^2 + 20*t - 5
sage: derivative(f, t, t)
-20*t^3 + 60*t^2 - 60*t + 20
sage: derivative(f, t, 2)
-20*t^3 + 60*t^2 - 60*t + 20
sage: derivative(f, 2)
-20*t^3 + 60*t^2 - 60*t + 20
We differentiate a symbolic expression:
sage: var('a x')
(a, x)
sage: f = exp(sin(a - x^2))/x
sage: derivative(f, x)
-2*e^(sin(-x^2 + a))*cos(-x^2 + a) - e^(sin(-x^2 + a))/x^2
sage: derivative(f, a)
e^(sin(-x^2 + a))*cos(-x^2 + a)/x
Syntax for repeated differentiation:
sage: R.<u, v> = PolynomialRing(QQ)
sage: f = u^4*v^5
sage: derivative(f, u)
4*u^3*v^5
sage: f.derivative(u) # can always use method notation too
4*u^3*v^5
sage: derivative(f, u, u)
12*u^2*v^5
sage: derivative(f, u, u, u)
24*u*v^5
sage: derivative(f, u, 3)
24*u*v^5
sage: derivative(f, u, v)
20*u^3*v^4
sage: derivative(f, u, 2, v)
60*u^2*v^4
sage: derivative(f, u, v, 2)
80*u^3*v^3
sage: derivative(f, [u, v, v])
80*u^3*v^3
EXAMPLES:
sage: a = (x-1)*(x^2 - 1); a
(x - 1)*(x^2 - 1)
sage: expand(a)
x^3 - x^2 - x + 1
You can also use expand on polynomial, integer, and other factorizations:
sage: x = polygen(ZZ)
sage: F = factor(x^12 - 1); F
(x - 1) * (x + 1) * (x^2 - x + 1) * (x^2 + 1) * (x^2 + x + 1) * (x^4 - x^2 + 1)
sage: expand(F)
x^12 - 1
sage: F.expand()
x^12 - 1
sage: F = factor(2007); F
3^2 * 223
sage: expand(F)
2007
Note: If you want to compute the expanded form of a polynomial arithmetic operation quickly and the coefficients of the polynomial all lie in some ring, e.g., the integers, it is vastly faster to create a polynomial ring and do the arithmetic there.
sage: x = polygen(ZZ) # polynomial over a given base ring.
sage: f = sum(x^n for n in range(5))
sage: f*f # much faster, even if the degree is huge
x^8 + 2*x^7 + 3*x^6 + 4*x^5 + 5*x^4 + 4*x^3 + 3*x^2 + 2*x + 1
TESTS:
sage: t1 = (sqrt(3)-3)*(sqrt(3)+1)/6;
sage: tt1 = -1/sqrt(3);
sage: t2 = sqrt(3)/6;
sage: float(t1)
-0.577350269189625...
sage: float(tt1)
-0.577350269189625...
sage: float(t2)
0.28867513459481287
sage: float(expand(t1 + t2))
-0.288675134594812...
sage: float(expand(tt1 + t2))
-0.288675134594812...
The integral of  .
.
EXAMPLES:
sage: integral(sin(x), x)
-cos(x)
sage: integral(sin(x)^2, x, pi, 123*pi/2)
121/4*pi
sage: integral( sin(x), x, 0, pi)
2
We integrate a symbolic function:
sage: f(x,y,z) = x*y/z + sin(z)
sage: integral(f, z)
(x, y, z) |--> x*y*log(z) - cos(z)
sage: var('a,b')
(a, b)
sage: assume(b-a>0)
sage: integral( sin(x), x, a, b)
cos(a) - cos(b)
sage: forget()
sage: integral(x/(x^3-1), x)
1/3*sqrt(3)*arctan(1/3*(2*x + 1)*sqrt(3)) + 1/3*log(x - 1) - 1/6*log(x^2 + x + 1)
sage: integral( exp(-x^2), x )
1/2*sqrt(pi)*erf(x)
We define the Gaussian, plot and integrate it numerically and symbolically:
sage: f(x) = 1/(sqrt(2*pi)) * e^(-x^2/2)
sage: P = plot(f, -4, 4, hue=0.8, thickness=2)
sage: P.show(ymin=0, ymax=0.4)
sage: numerical_integral(f, -4, 4) # random output
(0.99993665751633376, 1.1101527003413533e-14)
sage: integrate(f, x)
x |--> 1/2*erf(1/2*sqrt(2)*x)
You can have Sage calculate multiple integrals. For example,
consider the function 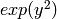 on the region between the
lines
on the region between the
lines 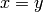 ,
, 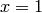 , and
, and 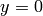 . We find the
value of the integral on this region using the command:
. We find the
value of the integral on this region using the command:
sage: area = integral(integral(exp(y^2),x,0,y),y,0,1); area
1/2*e - 1/2
sage: float(area)
0.859140914229522...
We compute the line integral of 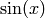 along the arc of
the curve
along the arc of
the curve 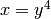 from
from 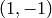 to
to
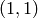 :
:
sage: t = var('t')
sage: (x,y) = (t^4,t)
sage: (dx,dy) = (diff(x,t), diff(y,t))
sage: integral(sin(x)*dx, t,-1, 1)
0
sage: restore('x,y') # restore the symbolic variables x and y
Sage is unable to do anything with the following integral:
sage: integral( exp(-x^2)*log(x), x )
integrate(e^(-x^2)*log(x), x)
Note, however, that:
sage: integral( exp(-x^2)*ln(x), x, 0, oo)
-1/4*(euler_gamma + 2*log(2))*sqrt(pi)
This definite integral is easy:
sage: integral( ln(x)/x, x, 1, 2)
1/2*log(2)^2
Sage can’t do this elliptic integral (yet):
sage: integral(1/sqrt(2*t^4 - 3*t^2 - 2), t, 2, 3)
integrate(1/sqrt(2*t^4 - 3*t^2 - 2), t, 2, 3)
A double integral:
sage: y = var('y')
sage: integral(integral(x*y^2, x, 0, y), y, -2, 2)
32/5
This illustrates using assumptions:
sage: integral(abs(x), x, 0, 5)
25/2
sage: integral(abs(x), x, 0, a)
integrate(abs(x), x, 0, a)
sage: assume(a>0)
sage: integral(abs(x), x, 0, a)
1/2*a^2
sage: forget() # forget the assumptions.
We integrate and differentiate a huge mess:
sage: f = (x^2-1+3*(1+x^2)^(1/3))/(1+x^2)^(2/3)*x/(x^2+2)^2
sage: g = integral(f, x)
sage: h = f - diff(g, x)
sage: [float(h(i)) for i in range(5)] #random
[0.0,
-1.1102230246251565e-16,
-5.5511151231257827e-17,
-5.5511151231257827e-17,
-6.9388939039072284e-17]
sage: h.factor()
0
sage: bool(h == 0)
True
The integral of  .
.
EXAMPLES:
sage: integral(sin(x), x)
-cos(x)
sage: integral(sin(x)^2, x, pi, 123*pi/2)
121/4*pi
sage: integral( sin(x), x, 0, pi)
2
We integrate a symbolic function:
sage: f(x,y,z) = x*y/z + sin(z)
sage: integral(f, z)
(x, y, z) |--> x*y*log(z) - cos(z)
sage: var('a,b')
(a, b)
sage: assume(b-a>0)
sage: integral( sin(x), x, a, b)
cos(a) - cos(b)
sage: forget()
sage: integral(x/(x^3-1), x)
1/3*sqrt(3)*arctan(1/3*(2*x + 1)*sqrt(3)) + 1/3*log(x - 1) - 1/6*log(x^2 + x + 1)
sage: integral( exp(-x^2), x )
1/2*sqrt(pi)*erf(x)
We define the Gaussian, plot and integrate it numerically and symbolically:
sage: f(x) = 1/(sqrt(2*pi)) * e^(-x^2/2)
sage: P = plot(f, -4, 4, hue=0.8, thickness=2)
sage: P.show(ymin=0, ymax=0.4)
sage: numerical_integral(f, -4, 4) # random output
(0.99993665751633376, 1.1101527003413533e-14)
sage: integrate(f, x)
x |--> 1/2*erf(1/2*sqrt(2)*x)
You can have Sage calculate multiple integrals. For example,
consider the function 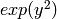 on the region between the
lines
on the region between the
lines 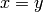 ,
, 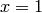 , and
, and 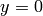 . We find the
value of the integral on this region using the command:
. We find the
value of the integral on this region using the command:
sage: area = integral(integral(exp(y^2),x,0,y),y,0,1); area
1/2*e - 1/2
sage: float(area)
0.859140914229522...
We compute the line integral of 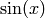 along the arc of
the curve
along the arc of
the curve 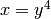 from
from 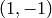 to
to
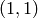 :
:
sage: t = var('t')
sage: (x,y) = (t^4,t)
sage: (dx,dy) = (diff(x,t), diff(y,t))
sage: integral(sin(x)*dx, t,-1, 1)
0
sage: restore('x,y') # restore the symbolic variables x and y
Sage is unable to do anything with the following integral:
sage: integral( exp(-x^2)*log(x), x )
integrate(e^(-x^2)*log(x), x)
Note, however, that:
sage: integral( exp(-x^2)*ln(x), x, 0, oo)
-1/4*(euler_gamma + 2*log(2))*sqrt(pi)
This definite integral is easy:
sage: integral( ln(x)/x, x, 1, 2)
1/2*log(2)^2
Sage can’t do this elliptic integral (yet):
sage: integral(1/sqrt(2*t^4 - 3*t^2 - 2), t, 2, 3)
integrate(1/sqrt(2*t^4 - 3*t^2 - 2), t, 2, 3)
A double integral:
sage: y = var('y')
sage: integral(integral(x*y^2, x, 0, y), y, -2, 2)
32/5
This illustrates using assumptions:
sage: integral(abs(x), x, 0, 5)
25/2
sage: integral(abs(x), x, 0, a)
integrate(abs(x), x, 0, a)
sage: assume(a>0)
sage: integral(abs(x), x, 0, a)
1/2*a^2
sage: forget() # forget the assumptions.
We integrate and differentiate a huge mess:
sage: f = (x^2-1+3*(1+x^2)^(1/3))/(1+x^2)^(2/3)*x/(x^2+2)^2
sage: g = integral(f, x)
sage: h = f - diff(g, x)
sage: [float(h(i)) for i in range(5)] #random
[0.0,
-1.1102230246251565e-16,
-5.5511151231257827e-17,
-5.5511151231257827e-17,
-6.9388939039072284e-17]
sage: h.factor()
0
sage: bool(h == 0)
True
Return the limit as the variable  approaches
approaches  from the given direction.
from the given direction.
limit(expr, x = a)
limit(expr, x = a, dir='above')
INPUT:
ALIAS: You can also use lim instead of limit.
EXAMPLES:
sage: limit(sin(x)/x, x=0)
1
sage: limit(exp(x), x=oo)
+Infinity
sage: lim(exp(x), x=-oo)
0
sage: lim(1/x, x=0)
Infinity
sage: limit(sqrt(x^2+x+1)+x, taylor=True, x=-oo)
-1/2
sage: limit((tan(sin(x)) - sin(tan(x)))/x^7, taylor=True, x=0)
1/30
Sage does not know how to do this limit (which is 0), so it returns it unevaluated:
sage: lim(exp(x^2)*(1-erf(x)), x=infinity)
limit(-e^(x^2)*erf(x) + e^(x^2), x, +Infinity)
Return the limit as the variable  approaches
approaches  from the given direction.
from the given direction.
limit(expr, x = a)
limit(expr, x = a, dir='above')
INPUT:
ALIAS: You can also use lim instead of limit.
EXAMPLES:
sage: limit(sin(x)/x, x=0)
1
sage: limit(exp(x), x=oo)
+Infinity
sage: lim(exp(x), x=-oo)
0
sage: lim(1/x, x=0)
Infinity
sage: limit(sqrt(x^2+x+1)+x, taylor=True, x=-oo)
-1/2
sage: limit((tan(sin(x)) - sin(tan(x)))/x^7, taylor=True, x=0)
1/30
Sage does not know how to do this limit (which is 0), so it returns it unevaluated:
sage: lim(exp(x^2)*(1-erf(x)), x=infinity)
limit(-e^(x^2)*erf(x) + e^(x^2), x, +Infinity)
Simplify the expression  .
.
EXAMPLES: We simplify the expression 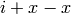 .
.
sage: f = I + x - x; simplify(f)
I
In fact, printing  yields the same thing - i.e., the
simplified form.
yields the same thing - i.e., the
simplified form.
Expands self in a truncated Taylor or Laurent series in the
variable  around the point
around the point  , containing terms
through
, containing terms
through 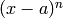 . Functions in more variables are also
supported.
. Functions in more variables are also
supported.
INPUT:
EXAMPLES:
sage: var('x,k,n')
(x, k, n)
sage: taylor (sqrt (1 - k^2*sin(x)^2), x, 0, 6)
-1/720*(45*k^6 - 60*k^4 + 16*k^2)*x^6 - 1/24*(3*k^4 - 4*k^2)*x^4 - 1/2*k^2*x^2 + 1
sage: taylor ((x + 1)^n, x, 0, 4)
1/24*(n^4 - 6*n^3 + 11*n^2 - 6*n)*x^4 + 1/6*(n^3 - 3*n^2 + 2*n)*x^3 + 1/2*(n^2 - n)*x^2 + n*x + 1
sage: taylor ((x + 1)^n, x, 0, 4)
1/24*(n^4 - 6*n^3 + 11*n^2 - 6*n)*x^4 + 1/6*(n^3 - 3*n^2 + 2*n)*x^3 + 1/2*(n^2 - n)*x^2 + n*x + 1
Taylor polynomial in two variables:
sage: x,y=var('x y'); taylor(x*y^3,(x,1),(y,-1),4)
(y + 1)^3*(x - 1) + (y + 1)^3 - 3*(y + 1)^2*(x - 1) - 3*(y + 1)^2 + 3*(y + 1)*(x - 1) - x + 3*y + 3