AUTHORS:
There are several ways to construct an elliptic curve:
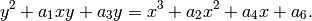
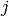 . Warning: this is deprecated. Use EllipticCurve_from_j(j)
or EllipticCurve(j=j) instead.
. Warning: this is deprecated. Use EllipticCurve_from_j(j)
or EllipticCurve(j=j) instead.EXAMPLES: We illustrate creating elliptic curves.
sage: EllipticCurve([0,0,1,-1,0])
Elliptic Curve defined by y^2 + y = x^3 - x over Rational Field
We create a curve from a Cremona label:
sage: EllipticCurve('37b2')
Elliptic Curve defined by y^2 + y = x^3 + x^2 - 1873*x - 31833 over Rational Field
sage: EllipticCurve('5077a')
Elliptic Curve defined by y^2 + y = x^3 - 7*x + 6 over Rational Field
sage: EllipticCurve('389a')
Elliptic Curve defined by y^2 + y = x^3 + x^2 - 2*x over Rational Field
We create curves over a finite field as follows:
sage: EllipticCurve([GF(5)(0),0,1,-1,0])
Elliptic Curve defined by y^2 + y = x^3 + 4*x over Finite Field of size 5
sage: EllipticCurve(GF(5), [0, 0,1,-1,0])
Elliptic Curve defined by y^2 + y = x^3 + 4*x over Finite Field of size 5
Elliptic curves over 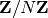 with
with 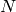 prime are of type
“elliptic curve over a finite field”:
prime are of type
“elliptic curve over a finite field”:
sage: F = Zmod(101)
sage: EllipticCurve(F, [2, 3])
Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Ring of integers modulo 101
sage: E = EllipticCurve([F(2), F(3)])
sage: type(E)
<class 'sage.schemes.elliptic_curves.ell_finite_field.EllipticCurve_finite_field'>
In contrast, elliptic curves over 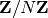 with
with 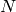 composite
are of type “generic elliptic curve”:
composite
are of type “generic elliptic curve”:
sage: F = Zmod(95)
sage: EllipticCurve(F, [2, 3])
Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Ring of integers modulo 95
sage: E = EllipticCurve([F(2), F(3)])
sage: type(E)
<class 'sage.schemes.elliptic_curves.ell_generic.EllipticCurve_generic'>
The following is a curve over the complex numbers:
sage: E = EllipticCurve(CC, [0,0,1,-1,0])
sage: E
Elliptic Curve defined by y^2 + 1.00000000000000*y = x^3 + (-1.00000000000000)*x over Complex Field with 53 bits of precision
sage: E.j_invariant()
2988.97297297297
We can also create elliptic curves by giving the Weierstrass equation:
sage: x, y = var('x,y')
sage: EllipticCurve(y^2 + y == x^3 + x - 9)
Elliptic Curve defined by y^2 + y = x^3 + x - 9 over Rational Field
sage: R.<x,y> = GF(5)[]
sage: EllipticCurve(x^3 + x^2 + 2 - y^2 - y*x)
Elliptic Curve defined by y^2 + x*y = x^3 + x^2 + 2 over Finite Field of size 5
We can explicitly specify the 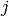 -invariant:
-invariant:
sage: E = EllipticCurve(j=1728); E; E.j_invariant(); E.label()
Elliptic Curve defined by y^2 = x^3 - x over Rational Field
1728
'32a2'
sage: E = EllipticCurve(j=GF(5)(2)); E; E.j_invariant()
Elliptic Curve defined by y^2 = x^3 + x + 1 over Finite Field of size 5
2
See trac #6657:
sage: EllipticCurve(GF(144169),j=1728)
Elliptic Curve defined by y^2 = x^3 + x over Finite Field of size 144169
TESTS:
sage: R = ZZ['u', 'v']
sage: EllipticCurve(R, [1,1])
Elliptic Curve defined by y^2 = x^3 + x + 1 over Multivariate Polynomial Ring in u, v
over Integer Ring
We create a curve and a point over QQbar (see #6879):
sage: E = EllipticCurve(QQbar,[0,1])
sage: E(0)
(0 : 1 : 0)
sage: E.base_field()
Algebraic Field
sage: E = EllipticCurve(RR,[1,2]); E; E.base_field()
Elliptic Curve defined by y^2 = x^3 + 1.00000000000000*x + 2.00000000000000 over Real Field with 53 bits of precision
Real Field with 53 bits of precision
sage: EllipticCurve(CC,[3,4]); E; E.base_field()
Elliptic Curve defined by y^2 = x^3 + 3.00000000000000*x + 4.00000000000000 over Complex Field with 53 bits of precision
Elliptic Curve defined by y^2 = x^3 + 1.00000000000000*x + 2.00000000000000 over Real Field with 53 bits of precision
Real Field with 53 bits of precision
sage: E = EllipticCurve(QQbar,[5,6]); E; E.base_field()
Elliptic Curve defined by y^2 = x^3 + 5*x + 6 over Algebraic Field
Algebraic Field
See trac #6657:
sage: EllipticCurve(3,j=1728)
...
ValueError: First parameter (if present) must be a ring when j is specified
sage: EllipticCurve(GF(5),j=3/5)
...
ValueError: First parameter must be a ring containing 3/5
Return an elliptic curve with given 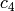 and
and
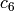 invariants.
invariants.
EXAMPLES:
sage: E = EllipticCurve_from_c4c6(17, -2005)
sage: E
Elliptic Curve defined by y^2 = x^3 - 17/48*x + 2005/864 over Rational Field
sage: E.c_invariants()
(17, -2005)
Construct an elliptic curve from a ternary cubic with a rational point.
INPUT:
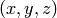 defining a projective point on the
curve
defining a projective point on the
curve 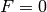 .
.OUTPUT:
(elliptic curve) An elliptic curve (in minimal Weierstrass form)
isomorphic to the curve 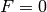 .
.
Note
USES MAGMA - This function will not work on computers that do not have magma installed.
TO DO: implement this without using MAGMA.
For a more general version, see the function EllipticCurve_from_plane_curve().
EXAMPLES:
First we find that the Fermat cubic is isomorphic to the curve with Cremona label 27a1:
sage: E = EllipticCurve_from_cubic('x^3 + y^3 + z^3', [1,-1,0]) # optional - magma
sage: E # optional - magma
Elliptic Curve defined by y^2 + y = x^3 - 7 over Rational Field
sage: E.cremona_label() # optional - magma
'27a1'
Next we find the minimal model and conductor of the Jacobian of the Selmer curve.
sage: E = EllipticCurve_from_cubic('u^3 + v^3 + 60*w^3', [1,-1,0]) # optional - magma
sage: E # optional - magma
Elliptic Curve defined by y^2 = x^3 - 24300 over Rational Field
sage: E.conductor() # optional - magma
24300
Return an elliptic curve with given 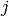 -invariant.
-invariant.
EXAMPLES:
sage: E = EllipticCurve_from_j(0); E; E.j_invariant(); E.label()
Elliptic Curve defined by y^2 + y = x^3 over Rational Field
0
'27a3'
sage: E = EllipticCurve_from_j(1728); E; E.j_invariant(); E.label()
Elliptic Curve defined by y^2 = x^3 - x over Rational Field
1728
'32a2'
sage: E = EllipticCurve_from_j(1); E; E.j_invariant()
Elliptic Curve defined by y^2 + x*y = x^3 + 36*x + 3455 over Rational Field
1
Construct an elliptic curve from a smooth plane cubic with a rational point.
INPUT:
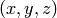 defining a projective point on the
curve C.
defining a projective point on the
curve C.OUTPUT:
(elliptic curve) An elliptic curve (in minimal Weierstrass form) isomorphic to C.
Note
USES MAGMA - This function will not work on computers that do not have magma installed.
TO DO: implement this without using MAGMA.
EXAMPLES:
First we check that the Fermat cubic is isomorphic to the curve with Cremona label ‘27a1’:
sage: x,y,z=PolynomialRing(QQ,3,'xyz').gens() # optional - magma
sage: C=Curve(x^3+y^3+z^3) # optional - magma
sage: P=C(1,-1,0) # optional - magma
sage: E=EllipticCurve_from_plane_curve(C,P) # optional - magma
sage: E # optional - magma
Elliptic Curve defined by y^2 + y = x^3 - 7 over Rational Field
sage: E.label() # optional - magma
'27a1'
Now we try a quartic example:
sage: u,v,w=PolynomialRing(QQ,3,'uvw').gens() # optional - magma
sage: C=Curve(u^4+u^2*v^2-w^4) # optional - magma
sage: P=C(1,0,1) # optional - magma
sage: E=EllipticCurve_from_plane_curve(C,P) # optional - magma
sage: E # optional - magma
Elliptic Curve defined by y^2 = x^3 + 4*x over Rational Field
sage: E.label() # optional - magma
'32a1'
Returns a sorted list of all elliptic curves defined over 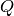 with good reduction outside the set
with good reduction outside the set  of primes.
of primes.
INPUT:
- S - list of primes (default: empty list).
- proof - True/False (default True): the MW basis for auxiliary curves will be computed with this proof flag.
- verbose - True/False (default False): if True, some details of the computation will be output.
Note
Proof flag: The algorithm used requires determining all S-integral points on several auxiliary curves, which in turn requires the computation of their generators. This is not always possible (even in theory) using current knowledge.
The value of this flag is passed to the function which computes generators of various auxiliary elliptic curves, in order to find their S-integral points. Set to False if the default (True) causes warning messages, but note that you can then not rely on the set of curves returned being complete.
EXAMPLES:
sage: EllipticCurves_with_good_reduction_outside_S([])
[]
sage: elist = EllipticCurves_with_good_reduction_outside_S([2])
sage: elist
[Elliptic Curve defined by y^2 = x^3 + 4*x over Rational Field,
Elliptic Curve defined by y^2 = x^3 - x over Rational Field,
...
Elliptic Curve defined by y^2 = x^3 - x^2 - 13*x + 21 over Rational Field]
sage: len(elist)
24
sage: ', '.join([e.label() for e in elist])
'32a1, 32a2, 32a3, 32a4, 64a1, 64a2, 64a3, 64a4, 128a1, 128a2, 128b1, 128b2, 128c1, 128c2, 128d1, 128d2, 256a1, 256a2, 256b1, 256b2, 256c1, 256c2, 256d1, 256d2'
Without the “Proof=False”, this example gives two warnings:
sage: elist = EllipticCurves_with_good_reduction_outside_S([11],proof=False)
sage: len(elist)
12
sage: ', '.join([e.label() for e in elist])
'11a1, 11a2, 11a3, 121a1, 121a2, 121b1, 121b2, 121c1, 121c2, 121d1, 121d2, 121d3'
sage: elist = EllipticCurves_with_good_reduction_outside_S([2,3]) # long time (~35s)
sage: len(elist) # long time
752
sage: max([e.conductor() for e in elist]) # long time
62208
sage: [N.factor() for N in Set([e.conductor() for e in elist])] # long time
[2^7,
2^8,
2^3 * 3^4,
2^2 * 3^3,
2^8 * 3^4,
2^4 * 3^4,
2^3 * 3,
2^7 * 3,
2^3 * 3^5,
3^3,
2^8 * 3,
2^5 * 3^4,
2^4 * 3,
2 * 3^4,
2^2 * 3^2,
2^6 * 3^4,
2^6,
2^7 * 3^2,
2^4 * 3^5,
2^4 * 3^3,
2 * 3^3,
2^6 * 3^3,
2^6 * 3,
2^5,
2^2 * 3^4,
2^3 * 3^2,
2^5 * 3,
2^7 * 3^4,
2^2 * 3^5,
2^8 * 3^2,
2^5 * 3^2,
2^7 * 3^5,
2^8 * 3^5,
2^3 * 3^3,
2^8 * 3^3,
2^5 * 3^5,
2^4 * 3^2,
2 * 3^5,
2^5 * 3^3,
2^6 * 3^5,
2^7 * 3^3,
3^5,
2^6 * 3^2]