Hyperelliptic curve constructor

sage.schemes.hyperelliptic_curves.constructor.HyperellipticCurve(f, h=None, names=None, PP=None)

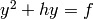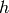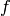Returns the hyperelliptic curve , for univariate polynomials and . If 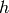is not given, then it defaults to 0.

INPUT:

• f - univariate polynomial
• h - optional univariate polynomial

EXAMPLES: A curve with and without the h term:

sage: R.<x> = QQ[]
sage: HyperellipticCurve(x^5 + x + 1)
Hyperelliptic Curve over Rational Field defined by y^2 = x^5 + x + 1
sage: HyperellipticCurve(x^19 + x + 1, x-2)
Hyperelliptic Curve over Rational Field defined by y^2 + (x - 2)*y = x^19 + x + 1

A curve over a non-prime finite field:

sage: k.<a> = GF(9); R.<x> = k[]
sage: HyperellipticCurve(x^3 + x - 1, x+a)
Hyperelliptic Curve over Finite Field in a of size 3^2 defined by y^2 + (x + a)*y = x^3 + x + 2

Here’s one where we change the names of the vars in the homogeneous polynomial:

sage: k.<a> = GF(9); R.<x> = k[]    
sage: HyperellipticCurve(x^3 + x - 1, x+a, names=['X','Y'])
Hyperelliptic Curve over Finite Field in a of size 3^2 defined by Y^2 + (X + a)*Y = X^3 + X + 2