Complex multiplication for elliptic curves

This module implements the functions

• hilbert_class_polynomial
• cm_j_invariants
• cm_j_invariants_and_orders

sage.schemes.elliptic_curves.cm.cm_j_invariants(K)

Return a list of all CM -invariants in the field .

INPUT:

• K – a number field (currently only implemented for )

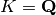OUTPUT:

(list) – A list of CM -invariants in the field .

Note

This is currently only implemented for the rationals. David Kohel has large tables for other fields, but they are not in Sage yet.

EXAMPLE:

sage: cm_j_invariants(QQ)
[0, 54000, -12288000, 1728, 287496, -3375, 16581375, 8000, -32768, -884736, -884736000, -147197952000, -262537412640768000]

sage: cm_j_invariants(QuadraticField(-1, 'i'))
...
NotImplementedError: Enumeration of CM j-invariants over Number Field in i with defining polynomial x^2 + 1 not yet implemented

sage.schemes.elliptic_curves.cm.cm_j_invariants_and_orders(K)

Return a list of all CM -invariants in the field , together with the associated orders.

INPUT:

• K – a number field (currently only implemented for )

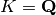OUTPUT:

(list) A list of 3-tuples 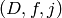where is a CM -invariant with quadratic fundamental discriminant and conductor

EXAMPLE:

sage: cm_j_invariants_and_orders(QQ)
[(-3, 3, -12288000), (-3, 2, 54000), (-3, 1, 0), (-4, 2, 287496), (-4, 1, 1728), (-7, 2, 16581375), (-7, 1, -3375), (-8, 1, 8000), (-11, 1, -32768), (-19, 1, -884736), (-43, 1, -884736000), (-67, 1, -147197952000), (-163, 1, -262537412640768000)]

sage: cm_j_invariants_and_orders(QuadraticField(-1, 'i'))
...
NotImplementedError: Enumeration of CM j-invariants over Number Field in i with defining polynomial x^2 + 1 not yet implemented

sage.schemes.elliptic_curves.cm.hilbert_class_polynomial(D, algorithm=None)

Returns the Hilbert class polynomial for discriminant .

INPUT:

• D (int) – a negative integer congruent to 0 or 1 modulo 4.
• algorithm (string, default None) – if “sage” then use the Sage implementation; if “magma” then call Magma (if available).

OUTPUT:

(integer polynomial) The Hilbert class polynomial for the discriminant .

ALGORITHM:

• If algorithm = “sage”: Use complex approximations to the roots.
• If algorithm = “magma”: Call the appropriate Magma function.

AUTHORS:

• Sage implementation originally by Eduardo Ocampo Alvarez and AndreyTimofeev
• Sage implementation corrected by John Cremona (using corrected precision bounds from Andreas Enge)
• Magma implementation by David Kohel

EXAMPLES:

sage: hilbert_class_polynomial(-4)
x - 1728
sage: hilbert_class_polynomial(-7)
x + 3375
sage: hilbert_class_polynomial(-23)
x^3 + 3491750*x^2 - 5151296875*x + 12771880859375
sage: hilbert_class_polynomial(-37*4)
x^2 - 39660183801072000*x - 7898242515936467904000000
sage: hilbert_class_polynomial(-37*4, algorithm="magma") # optional - magma
x^2 - 39660183801072000*x - 7898242515936467904000000
sage: hilbert_class_polynomial(-163)
x + 262537412640768000
sage: hilbert_class_polynomial(-163, algorithm="magma") # optional - magma
x + 262537412640768000