 space over a ring.¶
space over a ring.¶EXAMPLES: We construct projective space over various rings of various dimensions.
The simplest projective space:
sage: ProjectiveSpace(0)
Projective Space of dimension 0 over Integer Ring
A slightly bigger projective space over  :
:
sage: X = ProjectiveSpace(1000, QQ); X
Projective Space of dimension 1000 over Rational Field
sage: X.dimension()
1000
We can use “over” notation to create projective spaces over various base rings.
sage: X = ProjectiveSpace(5)/QQ; X
Projective Space of dimension 5 over Rational Field
sage: X/CC
Projective Space of dimension 5 over Complex Field with 53 bits of precision
The third argument specifies the printing names of the generators of the homogenous coordinate ring. Using objgens() you can obtain both the space and the generators as ready to use variables.
sage: P2, (x,y,z) = ProjectiveSpace(2, QQ, 'xyz').objgens()
sage: P2
Projective Space of dimension 2 over Rational Field
sage: x.parent()
Multivariate Polynomial Ring in x, y, z over Rational Field
For example, we use 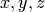 to define the intersection of
two lines.
to define the intersection of
two lines.
sage: V = P2.subscheme([x+y+z, x+y-z]); V
Closed subscheme of Projective Space of dimension 2 over Rational Field defined by:
x + y + z,
x + y - z
sage: V.dimension()
0
Return projective space of dimension  over the ring
over the ring  .
.
EXAMPLES: The dimension and ring can be given in either order.
sage: ProjectiveSpace(3, QQ)
Projective Space of dimension 3 over Rational Field
sage: ProjectiveSpace(5, QQ)
Projective Space of dimension 5 over Rational Field
sage: P = ProjectiveSpace(2, QQ, names='XYZ'); P
Projective Space of dimension 2 over Rational Field
sage: P.coordinate_ring()
Multivariate Polynomial Ring in X, Y, Z over Rational Field
The divide operator does base extension.
sage: ProjectiveSpace(5)/GF(17)
Projective Space of dimension 5 over Finite Field of size 17
The default base ring is  .
.
sage: ProjectiveSpace(5)
Projective Space of dimension 5 over Integer Ring
There is also an projective space associated each polynomial ring.
sage: R = GF(7)['x,y,z']
sage: P = ProjectiveSpace(R); P
Projective Space of dimension 2 over Finite Field of size 7
sage: P.coordinate_ring()
Multivariate Polynomial Ring in x, y, z over Finite Field of size 7
sage: P.coordinate_ring() is R
True
Projective spaces are not cached, i.e., there can be several with the same base ring and dimension (to facilitate gluing constructions).
Bases: sage.schemes.generic.projective_space.ProjectiveSpace_field
Return the list of 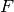 -rational points on the affine space self,
where
-rational points on the affine space self,
where 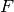 is a given finite field, or the base ring of self.
is a given finite field, or the base ring of self.
EXAMPLES:
sage: P = ProjectiveSpace(1, GF(3))
sage: P.rational_points()
[(0 : 1), (1 : 1), (2 : 1), (1 : 0)]
sage: P.rational_points(GF(3^2, 'b'))
[(0 : 1), (2*b : 1), (b + 1 : 1), (b + 2 : 1), (2 : 1), (b : 1), (2*b + 2 : 1), (2*b + 1 : 1), (1 : 1), (1 : 0)]
Bases: sage.schemes.generic.projective_space.ProjectiveSpace_field
Returns the projective points 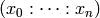 over
over
 with
with 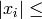 bound.
bound.
INPUT:
EXAMPLES:
sage: PP = ProjectiveSpace(0,QQ)
sage: PP.rational_points(1)
[(1)]
sage: PP = ProjectiveSpace(1,QQ)
sage: PP.rational_points(2)
[(-2 : 1), (-1 : 1), (0 : 1), (1 : 1), (2 : 1), (-1/2 : 1), (1/2 : 1), (1 : 0)]
sage: PP = ProjectiveSpace(2,QQ)
sage: PP.rational_points(2)
[(-2 : -2 : 1), (-1 : -2 : 1), (0 : -2 : 1), (1 : -2 : 1), (2 : -2 : 1),
(-2 : -1 : 1), (-1 : -1 : 1), (0 : -1 : 1), (1 : -1 : 1), (2 : -1 : 1),
(-2 : 0 : 1), (-1 : 0 : 1), (0 : 0 : 1), (1 : 0 : 1), (2 : 0 : 1), (-2 :
1 : 1), (-1 : 1 : 1), (0 : 1 : 1), (1 : 1 : 1), (2 : 1 : 1), (-2 : 2 :
1), (-1 : 2 : 1), (0 : 2 : 1), (1 : 2 : 1), (2 : 2 : 1), (-1/2 : -1 :
1), (1/2 : -1 : 1), (-1 : -1/2 : 1), (-1/2 : -1/2 : 1), (0 : -1/2 : 1),
(1/2 : -1/2 : 1), (1 : -1/2 : 1), (-1/2 : 0 : 1), (1/2 : 0 : 1), (-1 :
1/2 : 1), (-1/2 : 1/2 : 1), (0 : 1/2 : 1), (1/2 : 1/2 : 1), (1 : 1/2 :
1), (-1/2 : 1 : 1), (1/2 : 1 : 1), (-2 : 1 : 0), (-1 : 1 : 0), (0 : 1 :
0), (1 : 1 : 0), (2 : 1 : 0), (-1/2 : 1 : 0), (1/2 : 1 : 0), (1 : 0 :
0)]
Note
The very simple algorithm works as follows: every point
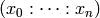 in projective space has a unique
largest index
in projective space has a unique
largest index  for which
for which 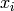 is not
zero. The algorithm then iterates downward on this
index. We normalize by choosing
is not
zero. The algorithm then iterates downward on this
index. We normalize by choosing 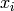 positive. Then,
the points
positive. Then,
the points 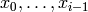 are the points of
affine
are the points of
affine  -space that are relatively prime to
-space that are relatively prime to
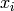 . We access these by using the Tuples method.
. We access these by using the Tuples method.
AUTHORS:
Bases: sage.schemes.generic.ambient_space.AmbientSpace
Projective space of dimension  over the ring
over the ring
 .
.
EXAMPLES:
sage: X.<x,y,z,w> = ProjectiveSpace(3, QQ)
sage: X.base_scheme()
Spectrum of Rational Field
sage: X.base_ring()
Rational Field
sage: X.structure_morphism ()
Scheme morphism:
From: Projective Space of dimension 3 over Rational Field
To: Spectrum of Rational Field
Defn: Structure map
sage: X.coordinate_ring()
Multivariate Polynomial Ring in x, y, z, w over Rational Field
Loading and saving:
sage: loads(X.dumps()) == X
True
Return the 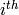 affine patch of this projective space.
This is an ambient affine space
affine patch of this projective space.
This is an ambient affine space 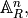 where
where
 is the base ring of self, whose “projective embedding”
map is
is the base ring of self, whose “projective embedding”
map is  in the
in the 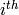 factor.
factor.
INPUT:
OUTPUT: an ambient affine space with fixed projective_embedding map.
EXAMPLES:
sage: PP = ProjectiveSpace(5) / QQ
sage: AA = PP.affine_patch(2)
sage: AA
Affine Space of dimension 5 over Rational Field
sage: AA.projective_embedding()
Scheme morphism:
From: Affine Space of dimension 5 over Rational Field
To: Projective Space of dimension 5 over Rational Field
Defn: Defined on coordinates by sending (x0, x1, x2, x3, x4) to
(x0 : x1 : 1 : x2 : x3 : x4)
sage: AA.projective_embedding(0)
Scheme morphism:
From: Affine Space of dimension 5 over Rational Field
To: Projective Space of dimension 5 over Rational Field
Defn: Defined on coordinates by sending (x0, x1, x2, x3, x4) to
(1 : x0 : x1 : x2 : x3 : x4)
Return a projective space over ring  and otherwise the same as self.
and otherwise the same as self.
INPUT:
OUTPUT:
Note
There is no need to have any relation between  and the base ring
of self, if you want to have such a relation, use
self.base_extend(R) instead.
and the base ring
of self, if you want to have such a relation, use
self.base_extend(R) instead.
EXAMPLES:
sage: P.<x, y, z> = ProjectiveSpace(2, ZZ)
sage: PQ = P.change_ring(QQ); PQ
Projective Space of dimension 2 over Rational Field
sage: PQ.change_ring(GF(5))
Projective Space of dimension 2 over Finite Field of size 5
Return the coordinate ring of this scheme.
EXAMPLES:
sage: ProjectiveSpace(3, GF(19^2,'alpha'), 'abcd').coordinate_ring()
Multivariate Polynomial Ring in a, b, c, d over Finite Field in alpha of size 19^2
sage: ProjectiveSpace(3).coordinate_ring()
Multivariate Polynomial Ring in x0, x1, x2, x3 over Integer Ring
sage: ProjectiveSpace(2, QQ, ['alpha', 'beta', 'gamma']).coordinate_ring()
Multivariate Polynomial Ring in alpha, beta, gamma over Rational Field
Return that this ambient space is projective n-space.
EXAMPLES:
sage: ProjectiveSpace(3,QQ).is_projective()
True
Return the number of generators of self, i.e. the number of variables in the coordinate ring of self.
EXAMPLES:
sage: ProjectiveSpace(3, QQ).ngens()
4
sage: ProjectiveSpace(7, ZZ).ngens()
8
Return the closed subscheme defined by X.
INPUT:
EXAMPLES:
sage: A.<x,y,z> = ProjectiveSpace(2, QQ)
sage: X = A.subscheme([x*z^2, y^2*z, x*y^2]); X
Closed subscheme of Projective Space of dimension 2 over Rational Field defined by:
x*z^2,
y^2*z,
x*y^2
sage: X.defining_polynomials ()
(x*z^2, y^2*z, x*y^2)
sage: I = X.defining_ideal(); I
Ideal (x*z^2, y^2*z, x*y^2) of Multivariate Polynomial Ring in x, y, z over Rational Field
sage: I.groebner_basis()
[x*y^2, y^2*z, x*z^2]
sage: X.dimension()
0
sage: X.base_ring()
Rational Field
sage: X.base_scheme()
Spectrum of Rational Field
sage: X.structure_morphism()
Scheme morphism:
From: Closed subscheme of Projective Space of dimension 2 over Rational Field defined by:
x*z^2,
y^2*z,
x*y^2
To: Spectrum of Rational Field
Defn: Structure map
Return True if  is a projective space, i.e., an ambient space
is a projective space, i.e., an ambient space
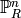 , where
, where  is a ring and
is a ring and 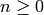 is an
integer.
is an
integer.
EXAMPLES:
sage: from sage.schemes.generic.projective_space import is_ProjectiveSpace
sage: is_ProjectiveSpace(ProjectiveSpace(5, names='x'))
True
sage: is_ProjectiveSpace(ProjectiveSpace(5, GF(9,'alpha'), names='x'))
True
sage: is_ProjectiveSpace(Spec(ZZ))
False