Scheme morphism

AUTHORS:

• David Kohel, William Stein
• William Stein (2006-02-11): fixed bug where P(0,0,0) was allowed as a projective point.

class sage.schemes.generic.morphism.PyMorphism(parent)

Bases: sage.structure.element.Element

category()

codomain()

domain()

is_endomorphism()

class sage.schemes.generic.morphism.SchemeMorphism(parent)

Bases: sage.schemes.generic.morphism.PyMorphism

A scheme morphism

glue_along_domains(other)

Assuming that self and other are open immersions with the same domain, return scheme obtained by gluing along the images.

EXAMPLES: We construct a scheme isomorphic to the projective line over 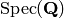by gluing two copies of 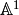minus a point.

sage: R.<x,y> = PolynomialRing(QQ, 2)
sage: S.<xbar, ybar> = R.quotient(x*y - 1)
sage: Rx = PolynomialRing(QQ, 'x')
sage: i1 = Rx.hom([xbar])
sage: Ry = PolynomialRing(QQ, 'y')
sage: i2 = Ry.hom([ybar])
sage: Sch = Schemes()
sage: f1 = Sch(i1)
sage: f2 = Sch(i2)

Now f1 and f2 have the same domain, which is a 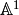minus a point. We glue along the domain:

sage: P1 = f1.glue_along_domains(f2)
sage: P1
Scheme obtained by gluing X and Y along U, where
  X: Spectrum of Univariate Polynomial Ring in x over Rational Field
  Y: Spectrum of Univariate Polynomial Ring in y over Rational Field
  U: Spectrum of Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x*y - 1)

sage: a, b = P1.gluing_maps()
sage: a
Affine Scheme morphism:
 From: Spectrum of Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x*y - 1)
  To:   Spectrum of Univariate Polynomial Ring in x over Rational Field
  Defn: Ring morphism:
          From: Univariate Polynomial Ring in x over Rational Field
          To:   Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x*y - 1)
          Defn: x |--> xbar
sage: b
Affine Scheme morphism:
  From: Spectrum of Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x*y - 1)
  To:   Spectrum of Univariate Polynomial Ring in y over Rational Field
  Defn: Ring morphism:
          From: Univariate Polynomial Ring in y over Rational Field
          To:   Quotient of Multivariate Polynomial Ring in x, y over Rational Field by the ideal (x*y - 1)
          Defn: y |--> ybar

class sage.schemes.generic.morphism.SchemeMorphism_abelian_variety_coordinates_field(X, v, check=True)

Bases: sage.structure.element.AdditiveGroupElement, sage.schemes.generic.morphism.SchemeMorphism_projective_coordinates_field

class sage.schemes.generic.morphism.SchemeMorphism_affine_coordinates(X, v, check=True)

Bases: sage.schemes.generic.morphism.SchemeMorphism_coordinates

A morphism determined by giving coordinates in a ring.

INPUT:

• X - a subscheme of an ambient affine space over a ring R.
• v - a list or tuple of coordinates in R

EXAMPLES:

sage: A = AffineSpace(2, QQ)
sage: A(1,2)
(1, 2)

class sage.schemes.generic.morphism.SchemeMorphism_coordinates(parent)

Bases: sage.schemes.generic.morphism.SchemeMorphism

scheme()

class sage.schemes.generic.morphism.SchemeMorphism_id(X)

Bases: sage.schemes.generic.morphism.SchemeMorphism

Return the identity morphism from X to itself.

EXAMPLES:

sage: X = Spec(ZZ)
sage: X.identity_morphism()
Scheme endomorphism of Spectrum of Integer Ring
  Defn: Identity map

class sage.schemes.generic.morphism.SchemeMorphism_on_points(parent, polys, check=True)

Bases: sage.schemes.generic.morphism.SchemeMorphism

A morphism of schemes determined by rational functions that define what the morphism does on points in the ambient space.

EXAMPLES: An example involving the affine plane:

sage: R.<x,y> = QQ[]
sage: A2 = AffineSpace(R)
sage: H = A2.Hom(A2)
sage: f = H([x-y, x*y])
sage: f([0,1])
(-1, 0)

An example involving the projective line:

sage: R.<x,y> = QQ[]
sage: P1 = ProjectiveSpace(R)
sage: H = P1.Hom(P1)
sage: f = H([x^2+y^2,x*y])
sage: f([0,1])
(1 : 0)

Some checks are performed to make sure the given polynomials define a morphism:

sage: R.<x,y> = QQ[]
sage: P1 = ProjectiveSpace(R)
sage: H = P1.Hom(P1)
sage: f = H([x^2, x*y])
...
ValueError: polys (=[x^2, x*y]) must not have common factors

sage: f = H([exp(x),exp(y)])
...
TypeError: polys (=[e^x, e^y]) must be elements of Multivariate Polynomial Ring in x, y over Rational Field

defining_polynomials()

Return the immutable sequence of polynomials that defines this scheme morphism.

EXAMPLES:

sage: R.<x,y> = QQ[]
sage: A.<x,y> = AffineSpace(R)
sage: H = A.Hom(A)
sage: H([x^3+y, 1-x-y]).defining_polynomials()
[x^3 + y, -x - y + 1]

class sage.schemes.generic.morphism.SchemeMorphism_on_points_affine_space(parent, polys, check=True)

Bases: sage.schemes.generic.morphism.SchemeMorphism_on_points

A morphism of schemes determined by rational functions that define what the morphism does on points in the ambient affine space.

EXAMPLES:

sage: RA.<x,y> = QQ[]
sage: A2 = AffineSpace(RA)
sage: RP.<u,v,w> = QQ[]
sage: P2 = ProjectiveSpace(RP)
sage: H = A2.Hom(P2)
sage: f = H([x, y, 1])
sage: f
Scheme morphism:
  From: Affine Space of dimension 2 over Rational Field
  To:   Projective Space of dimension 2 over Rational Field
  Defn: Defined on coordinates by sending (x, y) to
        (x : y : 1)

class sage.schemes.generic.morphism.SchemeMorphism_on_points_projective_space(parent, polys, check=True)

Bases: sage.schemes.generic.morphism.SchemeMorphism_on_points

A morphism of schemes determined by rational functions that define what the morphism does on points in the ambient projective space.

EXAMPLES:

sage: R.<x,y> = QQ[]
sage: P1 = ProjectiveSpace(R)
sage: H = P1.Hom(P1)
sage: H([y,2*x])
Scheme endomorphism of Projective Space of dimension 1 over Rational Field
  Defn: Defined on coordinates by sending (x : y) to
        (y : 2*x)

We illustrate some error checking:

sage: f = H([x-y, x*y])
...
ValueError: polys (=[x - y, x*y]) must be homogeneous of the same degree

sage: H([exp(x),exp(y)])
...
TypeError: polys (=[e^x, e^y]) must be elements of Multivariate Polynomial Ring in x, y over Rational Field

class sage.schemes.generic.morphism.SchemeMorphism_projective_coordinates_field(X, v, check=True)

Bases: sage.schemes.generic.morphism.SchemeMorphism_projective_coordinates_ring

A morphism determined by giving coordinates in a field.

INPUT:

• X - a subscheme of an ambient projective space over a field K
• v - a list or tuple of coordinates in K

EXAMPLES:

sage: P = ProjectiveSpace(3, RR)
sage: P(2,3,4,5)
(0.400000000000000 : 0.600000000000000 : 0.800000000000000 : 1.00000000000000)

sage: P = ProjectiveSpace(3, QQ)
sage: P(0,0,0,0)
...
ValueError: [0, 0, 0, 0] does not define a valid point since all entries are 0

class sage.schemes.generic.morphism.SchemeMorphism_projective_coordinates_ring(X, v, check=True)

Bases: sage.schemes.generic.morphism.SchemeMorphism_coordinates

A morphism determined by giving coordinates in a ring (how?).

class sage.schemes.generic.morphism.SchemeMorphism_spec(parent, phi, check=True)

Bases: sage.schemes.generic.morphism.SchemeMorphism

A morphism of spectrums of rings

EXAMPLES:

sage: R.<x> = PolynomialRing(QQ)
sage: phi = R.hom([QQ(7)]); phi
Ring morphism:
  From: Univariate Polynomial Ring in x over Rational Field
  To:   Rational Field
  Defn: x |--> 7

sage: X = Spec(QQ); Y = Spec(R)
sage: f = X.hom(phi); f
Affine Scheme morphism:
  From: Spectrum of Rational Field
  To:   Spectrum of Univariate Polynomial Ring in x over Rational Field
  Defn: Ring morphism:
          From: Univariate Polynomial Ring in x over Rational Field
          To:   Rational Field
          Defn: x |--> 7

sage: f.ring_homomorphism()
Ring morphism:
  From: Univariate Polynomial Ring in x over Rational Field
  To:   Rational Field
  Defn: x |--> 7

ring_homomorphism()

class sage.schemes.generic.morphism.SchemeMorphism_structure_map(parent)

Bases: sage.schemes.generic.morphism.SchemeMorphism

sage.schemes.generic.morphism.is_SchemeMorphism(f)

Return True if f is a scheme morphism or a point on an elliptic curve.

EXAMPLES:

sage: R.<x,y> = QQ[]; A.<x,y> = AffineSpace(R); H = A.Hom(A)
sage: f = H([y,x^2+y])
sage: sage.schemes.generic.morphism.is_SchemeMorphism(f)
True