Divisors on schemes

AUTHORS:

• William Stein
• David Kohel
• David Joyner

EXAMPLES:

sage: x,y,z = ProjectiveSpace(2, GF(5), names='x,y,z').gens()
sage: C = Curve(y^2*z^7 - x^9 - x*z^8)
sage: pts = C.rational_points(); pts
[(0 : 0 : 1), (0 : 1 : 0), (2 : 2 : 1), (2 : 3 : 1), (3 : 1 : 1), (3 : 4 : 1)]
sage: D1 = C.divisor(pts[0])*3
sage: D2 = C.divisor(pts[1])
sage: D3 = 10*C.divisor(pts[5])
sage: D1.parent() is D2.parent()
True
sage: D = D1 - D2 + D3; D
-(x, z) + 3*(x, y) + 10*(x + 2*z, y + z)
sage: D[1][0]
3
sage: D[1][1]
Ideal (x, y) of Multivariate Polynomial Ring in x, y, z over Finite Field of size 5
sage: C.divisor([(3, pts[0]), (-1, pts[1]), (10,pts[5])])
-(x, z) + 3*(x, y) + 10*(x + 2*z, y + z)

sage.schemes.generic.divisor.CurvePointToIdeal(C, P)

class sage.schemes.generic.divisor.Divisor_curve(v, check=True, reduce=True, parent=None)

Bases: sage.schemes.generic.divisor.Divisor_generic

For any curve , use C.divisor(v) to construct a divisor on . Here can be either

• a rational point on
• a list of rational points
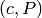• a list of 2-tuples , where is an integer and is a rational point.

TODO: Divisors shouldn’t be restricted to rational points. The problem is that the divisor group is the formal sum of the group of points on the curve, and there’s no implemented notion of point on 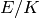that has coordinates in . This is what should be implemented, by adding an appropriate class to schemes/generic/morphism.py.

EXAMPLES:

sage: E = EllipticCurve([0, 0, 1, -1, 0])
sage: P = E(0,0)
sage: 10*P
(161/16 : -2065/64 : 1)
sage: D = E.divisor(P)
sage: D
(x, y)
sage: 10*D
10*(x, y)
sage: E.divisor([P, P])
2*(x, y)
sage: E.divisor([(3,P), (-4,5*P)])
3*(x, y) - 4*(x - 1/4*z, y + 5/8*z)

coeff(P)

Return the coefficient of a given point P in this divisor.

EXAMPLES:

sage: x,y = AffineSpace(2, GF(5), names='xy').gens()
sage: C = Curve(y^2 - x^9 - x)
sage: pts = C.rational_points(); pts
[(0, 0), (2, 2), (2, 3), (3, 1), (3, 4)]
sage: D = C.divisor(pts[0])
sage: D.coeff(pts[0])
1
sage: D = C.divisor([(3,pts[0]), (-1,pts[1])]); D
3*(x, y) - (x - 2, y - 2)
sage: D.coeff(pts[0])
3
sage: D.coeff(pts[1])
-1

support()

Return the support of this divisor, which is the set of points that occur in this divisor with nonzero coefficients.

EXAMPLES:

sage: x,y = AffineSpace(2, GF(5), names='xy').gens()
sage: C = Curve(y^2 - x^9 - x)
sage: pts = C.rational_points(); pts
[(0, 0), (2, 2), (2, 3), (3, 1), (3, 4)]
sage: D = C.divisor([(3,pts[0]), (-1, pts[1])]); D
3*(x, y) - (x - 2, y - 2)
sage: D.support()
[(0, 0), (2, 2)]

class sage.schemes.generic.divisor.Divisor_generic(v, check=True, reduce=True, parent=None)

Bases: sage.structure.formal_sum.FormalSum

scheme()

Return the scheme that this divisor is on.

EXAMPLES:

sage: A.<x, y> = AffineSpace(2, GF(5))
sage: C = Curve(y^2 - x^9 - x)
sage: pts = C.rational_points(); pts
[(0, 0), (2, 2), (2, 3), (3, 1), (3, 4)]
sage: D = C.divisor(pts[0])*3 - C.divisor(pts[1]); D
3*(x, y) - (x - 2, y - 2)
sage: D.scheme()
Affine Curve over Finite Field of size 5 defined by -x^9 + y^2 - x

sage.schemes.generic.divisor.is_Divisor(Div)

sage.schemes.generic.divisor.is_DivisorGroup(Div)