Let  be an elliptic curve defined over a number field
be an elliptic curve defined over a number field  (including
(including  ). We attach a period lattice (a discrete rank 2
subgroup of
). We attach a period lattice (a discrete rank 2
subgroup of 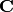 ) to each embedding of
) to each embedding of  into
into 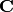 .
.
In the case of real embeddings, the lattice is stable under complex conjugation and is called a real lattice. These have two types: rectangular, (the real curve has two connected components and positive discriminant) or non-rectangular (one connected component, negative discriminant).
The periods are computed to arbitrary precision using the AGM (Gauss’s Arithmetic-Geometric Mean).
EXAMPLES:
sage: K.<a> = NumberField(x^3-2)
sage: E = EllipticCurve([0,1,0,a,a])
First we try a real embedding:
sage: emb = K.embeddings(RealField())[0]
sage: L = E.period_lattice(emb); L
Period lattice associated to Elliptic Curve defined by y^2 = x^3 + x^2 + a*x + a over Number Field in a with defining polynomial x^3 - 2 with respect to the embedding Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Algebraic Real Field
Defn: a |--> 1.259921049894873?
The first basis period is real:
sage: L.basis()
(3.81452977217855, 1.90726488608927 + 1.34047785962440*I)
sage: L.is_real()
True
For a basis 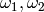 normalised so that
normalised so that 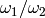 is in the fundamental region of the upper half-plane, use the function
normalised_basis() instead:
is in the fundamental region of the upper half-plane, use the function
normalised_basis() instead:
sage: L.normalised_basis()
(1.90726488608927 - 1.34047785962440*I, -1.90726488608927 - 1.34047785962440*I)
Next a complex embedding:
sage: emb = K.embeddings(ComplexField())[0]
sage: L = E.period_lattice(emb); L
Period lattice associated to Elliptic Curve defined by y^2 = x^3 + x^2 + a*x + a over Number Field in a with defining polynomial x^3 - 2 with respect to the embedding Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Algebraic Field
Defn: a |--> -0.6299605249474365? - 1.091123635971722?*I
In this case, the basis 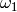 ,
, 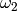 is always normalised so
that
is always normalised so
that  is in the fundamental region in the
upper half plane:
is in the fundamental region in the
upper half plane:
sage: w1,w2 = L.basis(); w1,w2
(-1.37588604166076 - 2.58560946624443*I, -2.10339907847356 + 0.428378776460622*I)
sage: L.is_real()
False
sage: tau = w1/w2; tau
0.387694505032876 + 1.30821088214407*I
sage: L.normalised_basis()
(-1.37588604166076 - 2.58560946624443*I, -2.10339907847356 + 0.428378776460622*I)
We test that bug #8415 (caused by a Pari bug fixed in v2.3.5) is OK:
sage: E = EllipticCurve('37a')
sage: K.<a> = QuadraticField(-7)
sage: EK = E.change_ring(K)
sage: EK.period_lattice(K.complex_embeddings()[0])
Period lattice associated to Elliptic Curve defined by y^2 + y = x^3 + (-1)*x over Number Field in a with defining polynomial x^2 + 7 with respect to the embedding Ring morphism:
From: Number Field in a with defining polynomial x^2 + 7
To: Algebraic Field
Defn: a |--> -2.645751311064591?*I
AUTHORS:
Bases: sage.modules.free_module.FreeModule_generic_pid
The class for the period lattice of an algebraic variety.
Bases: sage.schemes.elliptic_curves.period_lattice.PeriodLattice
The class for the period lattice of an elliptic curve.
Currently supported are elliptic curves defined over  , and
elliptic curves defined over a number field with a real or complex
embedding, where the lattice constructed depends on that
embedding.
, and
elliptic curves defined over a number field with a real or complex
embedding, where the lattice constructed depends on that
embedding.
Return a basis for this period lattice as a 2-tuple.
INPUT:
OUTPUT:
(tuple of Complex) 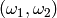 where the lattice is
where the lattice is
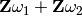 . If the lattice is real then
. If the lattice is real then
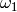 is real and positive,
is real and positive,  and
and
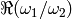 is either
is either 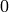 (for rectangular
lattices) or
(for rectangular
lattices) or  (for non-rectangular lattices).
Otherwise,
(for non-rectangular lattices).
Otherwise, 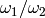 is in the fundamental region of
the upper half-plane. If the latter normalisation is required
for real lattices, use the function normalised_basis()
instead.
is in the fundamental region of
the upper half-plane. If the latter normalisation is required
for real lattices, use the function normalised_basis()
instead.
EXAMPLES:
sage: E = EllipticCurve('37a')
sage: E.period_lattice().basis()
(2.99345864623196, 2.45138938198679*I)
This shows that the issue reported at trac #3954 is fixed:
sage: E = EllipticCurve('37a')
sage: b1 = E.period_lattice().basis(prec=30)
sage: b2 = E.period_lattice().basis(prec=30)
sage: b1 == b2
True
This shows that the issue reported at trac #4064 is fixed:
sage: E = EllipticCurve('37a')
sage: E.period_lattice().basis(prec=30)[0].parent()
Real Field with 30 bits of precision
sage: E.period_lattice().basis(prec=100)[0].parent()
Real Field with 100 bits of precision
sage: K.<a> = NumberField(x^3-2)
sage: emb = K.embeddings(RealField())[0]
sage: E = EllipticCurve([0,1,0,a,a])
sage: L = E.period_lattice(emb)
sage: L.basis(64)
(3.81452977217854509, 1.90726488608927255 + 1.34047785962440202*I)
sage: emb = K.embeddings(ComplexField())[0]
sage: L = E.period_lattice(emb)
sage: w1,w2 = L.basis(); w1,w2
(-1.37588604166076 - 2.58560946624443*I, -2.10339907847356 + 0.428378776460622*I)
sage: L.is_real()
False
sage: tau = w1/w2; tau
0.387694505032876 + 1.30821088214407*I
Return the basis matrix of this period lattice.
INPUT:
OUTPUT:
A 2x2 real matrix whose rows are the lattice basis vectors,
after identifying 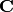 with
with 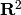 .
.
EXAMPLES:
sage: E = EllipticCurve('37a')
sage: E.period_lattice().basis_matrix()
[ 2.99345864623196 0.000000000000000]
[0.000000000000000 2.45138938198679]
sage: K.<a> = NumberField(x^3-2)
sage: emb = K.embeddings(RealField())[0]
sage: E = EllipticCurve([0,1,0,a,a])
sage: L = E.period_lattice(emb)
sage: L.basis_matrix(64)
[ 3.81452977217854509 0.000000000000000000]
[ 1.90726488608927255 1.34047785962440202]
See #4388:
sage: L = EllipticCurve('11a1').period_lattice()
sage: L.basis_matrix()
[ 1.26920930427955 0.000000000000000]
[0.634604652139777 1.45881661693850]
sage: L.basis_matrix(normalised=True)
[0.634604652139777 -1.45881661693850]
[-1.26920930427955 0.000000000000000]
sage: L = EllipticCurve('389a1').period_lattice()
sage: L.basis_matrix()
[ 2.49021256085505 0.000000000000000]
[0.000000000000000 1.97173770155165]
sage: L.basis_matrix(normalised=True)
[ 2.49021256085505 0.000000000000000]
[0.000000000000000 -1.97173770155165]
Return the area of a fundamental domain for the period lattice of the elliptic curve.
INPUT:
EXAMPLES:
sage: E = EllipticCurve('37a')
sage: E.period_lattice().complex_area()
7.33813274078958
sage: K.<a> = NumberField(x^3-2)
sage: embs = K.embeddings(ComplexField())
sage: E = EllipticCurve([0,1,0,a,a])
sage: [E.period_lattice(emb).is_real() for emb in K.embeddings(CC)]
[False, False, True]
sage: [E.period_lattice(emb).complex_area() for emb in embs]
[6.02796894766694, 6.02796894766694, 5.11329270448345]
Returns the coordinates of a complex number w.r.t. the lattice basis
INPUT:
z (complex) – A complex number.
output (see below).
OUTPUT:
When rounding is None (the default), returns a tuple
of reals  ,
, 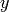 such that
such that 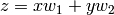 where
where  ,
,  are a basis for the lattice (normalised in the case of complex
embeddings).
are a basis for the lattice (normalised in the case of complex
embeddings).
When rounding is ‘round’, returns a tuple of integers 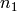 ,
,
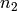 which are the closest integers to the
which are the closest integers to the  ,
, 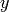 defined
above. If
defined
above. If  is in the lattice these are the coordinates of
is in the lattice these are the coordinates of
 with respect to the lattice basis.
with respect to the lattice basis.
When rounding is ‘floor’, returns a tuple of integers
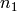 ,
, 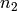 which are the integer parts to the
which are the integer parts to the  ,
, 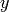 defined above. These are used in :meth:.reduce
defined above. These are used in :meth:.reduce
Return the elliptic curve associated with this period lattice.
EXAMPLES:
sage: E = EllipticCurve('37a')
sage: L = E.period_lattice()
sage: L.curve() is E
True
sage: K.<a> = NumberField(x^3-2)
sage: E = EllipticCurve([0,1,0,a,a])
sage: L = E.period_lattice(K.embeddings(RealField())[0])
sage: L.curve() is E
True
sage: L = E.period_lattice(K.embeddings(ComplexField())[0])
sage: L.curve() is E
True
Return the x-coordinates of the 2-division points of the elliptic curve associated with this period lattice, as elements of QQbar.
EXAMPLES:
sage: E = EllipticCurve('37a')
sage: L = E.period_lattice()
sage: L.ei()
[-1.107159871688768?, 0.2695944364054446?, 0.8375654352833230?]
sage: K.<a> = NumberField(x^3-2)
sage: E = EllipticCurve([0,1,0,a,a])
sage: L = E.period_lattice(K.embeddings(RealField())[0])
sage: L.ei()
[0.?e-19 - 1.122462048309373?*I, 0.?e-19 + 1.122462048309373?*I, -1]
sage: L = E.period_lattice(K.embeddings(ComplexField())[0]) sage: L.ei() [-1.000000000000000? + 0.?e-1...*I, -0.9720806486198328? - 0.561231024154687?*I, 0.9720806486198328? + 0.561231024154687?*I]
Return the elliptic exponential of a complex number.
INPUT:
OUTPUT:
(Either an elliptic curve point, or a 2-tuple of real or
complex numbers). The elliptic exponential of  modulo this
period lattice. If to_curve is False this is the pair
modulo this
period lattice. If to_curve is False this is the pair
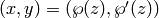 where
where 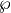 denotes the Weierstrass
function with respect to this lattice. If to_curve is
True it is the point with coordinates
denotes the Weierstrass
function with respect to this lattice. If to_curve is
True it is the point with coordinates
 as a point in
as a point in 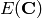 .
.
If the lattice is real and  is also real then the output is
a pair of real numbers (if to_curve is True), or a point in
is also real then the output is
a pair of real numbers (if to_curve is True), or a point in
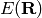 if to_curve is False.
if to_curve is False.
Note
The precision is taken from that of the input z.
EXAMPLES:
sage: E = EllipticCurve([1,1,1,-8,6])
sage: P = E(0,2)
sage: L = E.period_lattice()
sage: z = L(P); z
2.65289807021917
sage: L.elliptic_exponential(z)
(1.06...e-15 : 2.00000000000000 : 1.00000000000000)
sage: _.curve()
Elliptic Curve defined by y^2 + 1.00000000000000*x*y + 1.00000000000000*y = x^3 + 1.00000000000000*x^2 - 8.00000000000000*x + 6.00000000000000 over Real Field with 53 bits of precision
sage: L.elliptic_exponential(z,False)
(0.416666666666668, 2.50000000000000)
sage: z = L(P,prec=200); z
2.6528980702191653584337189314791830484705213985544997536510
sage: L.elliptic_exponential(z)
(-1.0773...e-60 : 2.0000000000000000000000000000000000000000000000000000000000 : 1.0000000000000000000000000000000000000000000000000000000000)
Return the elliptic logarithm of a point.
INPUT:
P (point) – A point on the elliptic curve associated with this period lattice.
(default real precision if None).
OUTPUT:
(complex number) The elliptic logarithm of the point 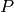 with
respect to this period lattice. If
with
respect to this period lattice. If  is the elliptic curve
and
is the elliptic curve
and 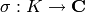 the embedding, the the returned value
the embedding, the the returned value  is such that
is such that 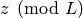 maps to
maps to 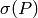 under the
standard Weierstrass isomorphism from
under the
standard Weierstrass isomorphism from 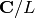 to
to 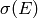 .
The output is reduced: it is in the fundamental period
parallelogram with respect to the normalised lattice basis.
.
The output is reduced: it is in the fundamental period
parallelogram with respect to the normalised lattice basis.
EXAMPLES:
sage: E = EllipticCurve('389a')
sage: L = E.period_lattice()
sage: E.discriminant() > 0
True
sage: L.real_flag
1
sage: P = E([-1,1])
sage: P.is_on_identity_component ()
False
sage: L.elliptic_logarithm(P, prec=96)
0.4793482501902193161295330101 + 0.9858688507758241022112038491*I
sage: Q=E([3,5])
sage: Q.is_on_identity_component()
True
sage: L.elliptic_logarithm(Q, prec=96)
1.931128271542559442488585220
Note that this is actually the inverse of the Weierstrass isomorphism:
sage: pari(E).ellztopoint(_)
[3.00000000000000 + 0.E-18*I, 5.00000000000000 + 0.E-18*I]
An example with negative discriminant, and a torsion point:
sage: E = EllipticCurve('11a1')
sage: L = E.period_lattice()
sage: E.discriminant() < 0
True
sage: L.real_flag
-1
sage: P = E([16,-61])
sage: L.elliptic_logarithm(P)
0.253841860855911
sage: L.real_period() / L.elliptic_logarithm(P)
5.00000000000000
An example where precision is problematic:
sage: E = EllipticCurve([1, 0, 1, -85357462, 303528987048]) #18074g1 sage: P = E([4458713781401/835903744, -64466909836503771/24167649046528, 1]) sage: L = E.period_lattice() sage: L.ei() [5334.003952567705? - 1.964393150436?e-6*I, 5334.003952567705? + 1.964393150436?e-6*I, -10668.25790513541?] sage: L.elliptic_logarithm(P,prec=100) 0.27656204014107061464076203097
Some complex exampes, taken from the paper by Cremona and Thongjunthug:
sage: K.<i> = QuadraticField(-1)
sage: a4 = 9*i-10
sage: a6 = 21-i
sage: E = EllipticCurve([0,0,0,a4,a6])
sage: e1 = 3-2*i; e2 = 1+i; e3 = -4+i
sage: emb = K.embeddings(CC)[1]
sage: L = E.period_lattice(emb)
sage: P = E(2-i,4+2*i)
sage: L.elliptic_logarithm(P,prec=100)
0.70448375537782208460499649302 - 0.79246725643650979858266018068*I
sage: L.elliptic_logarithm(E(e1,0),prec=100)
0.64607575874356525952487867052 + 0.22379609053909448304176885364*I
sage: L.elliptic_logarithm(E(e2,0),prec=100)
0.71330686725892253793705940192 - 0.40481924028150941053684639367*I
sage: L.elliptic_logarithm(E(e3,0),prec=100)
0.067231108515357278412180731396 - 0.62861533082060389357861524731*I
sage: L.coordinates(2*L.elliptic_logarithm(E(e1,0),prec=100))
(1.0000000000000000000000000000, 0.00000000000000000000000000000)
sage: L.coordinates(2*L.elliptic_logarithm(E(e2,0),prec=100))
(1.0000000000000000000000000000, 1.0000000000000000000000000000)
sage: L.coordinates(2*L.elliptic_logarithm(E(e3,0),prec=100))
(0.00000000000000000000000000000, 1.0000000000000000000000000000)
sage: a4 = -78*i + 104
sage: a6 = -216*i - 312
sage: E = EllipticCurve([0,0,0,a4,a6])
sage: emb = K.embeddings(CC)[1]
sage: L = E.period_lattice(emb)
sage: P = E(3+2*i,14-7*i)
sage: L.elliptic_logarithm(P)
0.297147783912228 - 0.546125549639461*I
sage: L.coordinates(L.elliptic_logarithm(P))
(0.628653378040238, 0.371417754610223)
sage: e1 = 1+3*i; e2 = -4-12*i; e3=-e1-e2
sage: L.coordinates(L.elliptic_logarithm(E(e1,0)))
(0.500000000000000, 0.500000000000000)
sage: L.coordinates(L.elliptic_logarithm(E(e2,0)))
(1.00000000000000, 0.500000000000000)
sage: L.coordinates(L.elliptic_logarithm(E(e3,0)))
(0.500000000000000, 0.000000000000000)
Return True if this period lattice is real.
EXAMPLES:
sage: f = EllipticCurve('11a')
sage: f.period_lattice().is_real()
True
sage: K.<i> = QuadraticField(-1)
sage: E = EllipticCurve(K,[0,0,0,i,2*i])
sage: emb = K.embeddings(ComplexField())[0]
sage: L = E.period_lattice(emb)
sage: L.is_real()
False
sage: K.<a> = NumberField(x^3-2)
sage: E = EllipticCurve([0,1,0,a,a])
sage: [E.period_lattice(emb).is_real() for emb in K.embeddings(CC)]
[False, False, True]
ALGORITHM:
The lattice is real if it is associated to a real embedding; such lattices are stable under conjugation.
Return True if this period lattice is rectangular.
Note
Only defined for real lattices; a RuntimeError is raised for non-real lattices.
EXAMPLES:
sage: f = EllipticCurve('11a')
sage: f.period_lattice().basis()
(1.26920930427955, 0.634604652139777 + 1.45881661693850*I)
sage: f.period_lattice().is_rectangular()
False
sage: f = EllipticCurve('37b')
sage: f.period_lattice().basis()
(1.08852159290423, 1.76761067023379*I)
sage: f.period_lattice().is_rectangular()
True
ALGORITHM:
The period lattice is rectangular precisely if the discriminant of the Weierstrass equation is positive, or equivalently if the number of real components is 2.
Return a normalised basis for this period lattice as a 2-tuple.
INPUT:
OUTPUT:
(tuple of Complex) 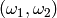 where the lattice has
the form
where the lattice has
the form 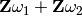 . The basis is normalised
so that
. The basis is normalised
so that 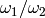 is in the fundamental region of
the upper half-plane. For an alternative normalisation for
real lattices (with the first period real), use the function
basis() instead.
is in the fundamental region of
the upper half-plane. For an alternative normalisation for
real lattices (with the first period real), use the function
basis() instead.
EXAMPLES:
sage: E = EllipticCurve('37a')
sage: E.period_lattice().normalised_basis()
(2.99345864623196, -2.45138938198679*I)
sage: K.<a> = NumberField(x^3-2)
sage: emb = K.embeddings(RealField())[0]
sage: E = EllipticCurve([0,1,0,a,a])
sage: L = E.period_lattice(emb)
sage: L.normalised_basis(64)
(1.90726488608927255 - 1.34047785962440202*I, -1.90726488608927255 - 1.34047785962440202*I)
sage: emb = K.embeddings(ComplexField())[0]
sage: L = E.period_lattice(emb)
sage: w1,w2 = L.normalised_basis(); w1,w2
(-1.37588604166076 - 2.58560946624443*I, -2.10339907847356 + 0.428378776460622*I)
sage: L.is_real()
False
sage: tau = w1/w2; tau
0.387694505032876 + 1.30821088214407*I
Returns the real or complex volume of this period lattice.
INPUT:
OUTPUT:
(real) For real lattices, this is the real period times the number of connected components. For non-real lattices it is the complex area.
Note
If the curve is defined over  and is given by a
minimal Weierstrass equation, then this is the correct
period in the BSD conjecture, i.e., it is the least real
period * 2 when the period lattice is rectangular. More
generally the product of this quantity over all embeddings
appears in the generalised BSD formula.
and is given by a
minimal Weierstrass equation, then this is the correct
period in the BSD conjecture, i.e., it is the least real
period * 2 when the period lattice is rectangular. More
generally the product of this quantity over all embeddings
appears in the generalised BSD formula.
EXAMPLES:
sage: E = EllipticCurve('37a')
sage: E.period_lattice().omega()
5.98691729246392
This is not a minimal model:
sage: E = EllipticCurve([0,-432*6^2])
sage: E.period_lattice().omega()
0.486109385710056
If you were to plug the above omega into the BSD conjecture, you would get nonsense. The following works though:
sage: F = E.minimal_model()
sage: F.period_lattice().omega()
0.972218771420113
sage: K.<a> = NumberField(x^3-2)
sage: emb = K.embeddings(RealField())[0]
sage: E = EllipticCurve([0,1,0,a,a])
sage: L = E.period_lattice(emb)
sage: L.omega(64)
3.81452977217854509
A complex example (taken from J.E.Cremona and E.Whitley, Periods of cusp forms and elliptic curves over imaginary quadratic fields, Mathematics of Computation 62 No. 205 (1994), 407-429):
sage: K.<i> = QuadraticField(-1)
sage: E = EllipticCurve([0,1-i,i,-i,0])
sage: L = E.period_lattice(K.embeddings(CC)[0])
sage: L.omega()
8.80694160502647
Returns the real period of this period lattice.
INPUT:
Note
Only defined for real lattices; a RuntimeError is raised for non-real lattices.
EXAMPLES:
sage: E = EllipticCurve('37a')
sage: E.period_lattice().real_period()
2.99345864623196
sage: K.<a> = NumberField(x^3-2)
sage: emb = K.embeddings(RealField())[0]
sage: E = EllipticCurve([0,1,0,a,a])
sage: L = E.period_lattice(emb)
sage: L.real_period(64)
3.81452977217854509
Reduce a complex number modulo the lattice
INPUT:
- z (complex) – A complex number.
OUTPUT:
(complex) the reduction of  modulo the lattice, lying in
the fundamental period parallelogram with respect to the
lattice basis. For curves defined over the reals (i.e. real
embeddings) the output will be real when possible.
modulo the lattice, lying in
the fundamental period parallelogram with respect to the
lattice basis. For curves defined over the reals (i.e. real
embeddings) the output will be real when possible.
Returns the value of the Weierstrass sigma function for this elliptic curve period lattice.
INPUT:
z – a complex number
(default real precision if None).
flag –
0: (default) ???;
1: computes an arbitrary determination of log(sigma(z))
2, 3: same using the product expansion instead of theta series. ???
Note
The reason for the ???’s above, is that the PARI
documentation for ellsigma is very vague. Also this is
only implemented for curves defined over  .
.
TODO:
This function does not use any of the PeriodLattice functions and so should be moved to ell_rational_field.
EXAMPLES:
sage: EllipticCurve('389a1').period_lattice().sigma(CC(2,1))
2.60912163570108 - 0.200865080824587*I
Internal function for the extended AGM used in elliptic logarithm computation. INPUT:
OUTPUT:
(3-tuple) 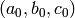 , the limit of the iteration
, the limit of the iteration 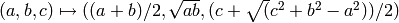 .
.
EXAMPLES:
sage: from sage.schemes.elliptic_curves.period_lattice import extended_agm_iteration
sage: extended_agm_iteration(RR(1),RR(2),RR(3))
(1.45679103104691, 1.45679103104691, 3.21245294970054)
sage: extended_agm_iteration(CC(1,2),CC(2,3),CC(3,4))
(1.46242448156430 + 2.47791311676267*I,
1.46242448156430 + 2.47791311676267*I,
3.22202144343535 + 4.28383734262540*I)
TESTS:
sage: extended_agm_iteration(1,2,3)
...
ValueError: values must be real or complex numbers
Normalise the period basis  so that
so that 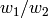 is in the fundamental region.
is in the fundamental region.
INPUT:
OUTPUT:
(tuple) ![((\omega_1',\omega_2'),[a,b,c,d])](../../../_images/math/73944374486fd0bde0e173cd9833593b23c72648.png) where
where 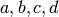 are
integers such that
are
integers such that
;
;
is in the upper half plane;
and
.
EXAMPLES:
sage: from sage.schemes.elliptic_curves.period_lattice import reduce_tau, normalise_periods
sage: w1 = CC(1.234, 3.456)
sage: w2 = CC(1.234, 3.456000001)
sage: w1/w2 # in lower half plane!
0.999999999743367 - 9.16334785827644e-11*I
sage: w1w2, abcd = normalise_periods(w1,w2)
sage: a,b,c,d = abcd
sage: w1w2 == (a*w1+b*w2, c*w1+d*w2)
True
sage: w1w2[0]/w1w2[1]
1.23400010389203e9*I
sage: a*d-b*c # note change of orientation
-1
Transform a point in the upper half plane to the fundamental region.
INPUT:
OUTPUT:
(tuple) ![(\tau',[a,b,c,d])](../../../_images/math/48d5ff56914ee077cbde67b02770fa2cf7977377.png) where
where 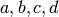 are integers such that
are integers such that
;
;
;
.
EXAMPLES:
sage: from sage.schemes.elliptic_curves.period_lattice import reduce_tau
sage: reduce_tau(CC(1.23,3.45))
(0.230000000000000 + 3.45000000000000*I, [1, -1, 0, 1])
sage: reduce_tau(CC(1.23,0.0345))
(-0.463960069171512 + 1.35591888067914*I, [-5, 6, 4, -5])
sage: reduce_tau(CC(1.23,0.0000345))
(0.130000000001761 + 2.89855072463768*I, [13, -16, 100, -123])