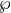 function for elliptic curves.¶
function for elliptic curves.¶The Weierstrass 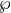 function associated to an elliptic curve over a field
function associated to an elliptic curve over a field  is a Laurent series
of the form
is a Laurent series
of the form
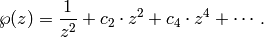
If the field is contained in 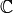 , then
this is the series expansion of the map from
, then
this is the series expansion of the map from 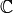 to
to 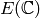 whose kernel is the period lattice of
whose kernel is the period lattice of  .
.
Over other fields, like finite fields, this still makes sense as a formal power series with coefficients in  - at least its first
- at least its first 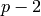 coefficients where
coefficients where  is the characteristic of
is the characteristic of  . It can be defined via the formal group as
. It can be defined via the formal group as 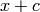 in the variable
in the variable 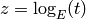 for a constant
for a constant  such that the constant term
such that the constant term 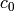 in
in 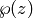 is zero.
is zero.
EXAMPLE:
sage: E = EllipticCurve([0,1])
sage: E.weierstrass_p()
z^-2 - 1/7*z^4 + 1/637*z^10 - 1/84721*z^16 + O(z^20)
REFERENCES:
AUTHORS:
Computes the Weierstrass function of an elliptic curve defined by short Weierstrass model: 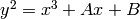 . It does this with as fast as polynomial of degree
. It does this with as fast as polynomial of degree  can be multiplied together in the base ring, i.e.
can be multiplied together in the base ring, i.e. 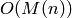 in the notation of [BMSS].
in the notation of [BMSS].
Let  be the characteristic of the underlying field: Then we must have either
be the characteristic of the underlying field: Then we must have either 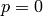 , or
, or 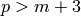 .
.
INPUT:
- k - the base field of the curve
- A - and
- B - as the coeffients of the short Weierstrass model
, and
- m - the precision to which the function is computed to.
OUTPUT:
the Weierstrass 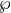 function as a Laurent series to precision
function as a Laurent series to precision  .
.
ALGORITHM:
This function uses the algorithm described in section 3.3 of [BMSS].
EXAMPLES:
sage: from sage.schemes.elliptic_curves.ell_wp import compute_wp_fast
sage: compute_wp_fast(QQ, 1, 8, 7)
z^-2 - 1/5*z^2 - 8/7*z^4 + 1/75*z^6 + O(z^7)
sage: k = GF(37)
sage: compute_wp_fast(k, k(1), k(8), 5)
z^-2 + 22*z^2 + 20*z^4 + O(z^5)
Computes the Weierstrass 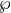 -function via calling the corresponding function in pari.
-function via calling the corresponding function in pari.
EXAMPLES:
sage: E = EllipticCurve([0,1])
sage: E.weierstrass_p(algorithm='pari')
z^-2 - 1/7*z^4 + 1/637*z^10 - 1/84721*z^16 + O(z^20)
sage: E = EllipticCurve(GF(101),[5,4])
sage: E.weierstrass_p(prec=30, algorithm='pari')
z^-2 + 100*z^2 + 86*z^4 + 34*z^6 + 50*z^8 + 82*z^10 + 45*z^12 + 70*z^14 + 33*z^16 + 87*z^18 + 33*z^20 + 36*z^22 + 45*z^24 + 40*z^26 + 12*z^28 + O(z^30)
sage: from sage.schemes.elliptic_curves.ell_wp import compute_wp_pari
sage: compute_wp_pari(E, prec= 20)
z^-2 + 100*z^2 + 86*z^4 + 34*z^6 + 50*z^8 + 82*z^10 + 45*z^12 + 70*z^14 + 33*z^16 + 87*z^18 + O(z^20)
Computes the truncated Weierstrass function of an elliptic curve defined by short Weierstrass model: 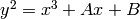 . Uses an algorithm that is of complexity
. Uses an algorithm that is of complexity 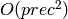 .
.
Let p be the characteristic of the underlying field: Then we must have either p=0, or p > prec + 3.
INPUT:
- k - the field of definition of the curve
- A - and
- B - the coefficients of the elliptic curve
- prec - the precision to which we compute the series.
OUTPUT:
A Laurent series aproximating the Weierstrass 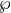 -function to precision prec.
-function to precision prec.
ALGORITHM: This function uses the algorithm described in section 3.2 of [BMSS].
REFERENCES: [BMSS] Boston, Morain, Salvy, Schost, “Fast Algorithms for Isogenies.”
EXAMPLES:
sage: E = EllipticCurve([7,0])
sage: E.weierstrass_p(prec=10, algorithm='quadratic')
z^-2 - 7/5*z^2 + 49/75*z^6 + O(z^10)
sage: E = EllipticCurve(GF(103),[1,2])
sage: E.weierstrass_p(algorithm='quadratic')
z^-2 + 41*z^2 + 88*z^4 + 11*z^6 + 57*z^8 + 55*z^10 + 73*z^12 + 11*z^14 + 17*z^16 + 50*z^18 + O(z^20)
sage: from sage.schemes.elliptic_curves.ell_wp import compute_wp_quadratic
sage: compute_wp_quadratic(E.base_ring(), E.a4(), E.a6(), prec=10)
z^-2 + 41*z^2 + 88*z^4 + 11*z^6 + 57*z^8 + O(z^10)
Solves a system of linear differential equations: 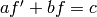 and
and 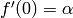 where
where  ,
,  , and
, and  are power series in one variable and
are power series in one variable and  is a constant in the coefficient ring.
is a constant in the coefficient ring.
ALGORITHM:
due to Brent and Kung ‘78.
EXAMPLES:
sage: from sage.schemes.elliptic_curves.ell_wp import solve_linear_differential_system
sage: k = GF(17)
sage: R.<x> = PowerSeriesRing(k)
sage: a = 1+x+O(x^7); b = x+O(x^7); c = 1+x^3+O(x^7); alpha = k(3)
sage: f = solve_linear_differential_system(a,b,c,alpha)
sage: f
3 + x + 15*x^2 + x^3 + 10*x^5 + 3*x^6 + 13*x^7 + O(x^8)
sage: a*f.derivative()+b*f - c
O(x^7)
sage: f(0) == alpha
True
Computes the Weierstrass 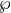 -function on an elliptic curve.
-function on an elliptic curve.
INPUT:
OUTPUT:
a Laurent series in one variable  with coefficients in the base field
with coefficients in the base field  of
of  .
.
EXAMPLES:
sage: E = EllipticCurve('11a1')
sage: E.weierstrass_p(prec=10)
z^-2 + 31/15*z^2 + 2501/756*z^4 + 961/675*z^6 + 77531/41580*z^8 + O(z^10)
sage: E.weierstrass_p(prec=8)
z^-2 + 31/15*z^2 + 2501/756*z^4 + 961/675*z^6 + O(z^8)
sage: Esh = E.short_weierstrass_model()
sage: Esh.weierstrass_p(prec=8)
z^-2 + 13392/5*z^2 + 1080432/7*z^4 + 59781888/25*z^6 + O(z^8)
sage: E.weierstrass_p(prec=8, algorithm='pari')
z^-2 + 31/15*z^2 + 2501/756*z^4 + 961/675*z^6 + O(z^8)
sage: E.weierstrass_p(prec=8, algorithm='quadratic')
z^-2 + 31/15*z^2 + 2501/756*z^4 + 961/675*z^6 + O(z^8)
sage: k = GF(11)
sage: E = EllipticCurve(k, [1,1])
sage: E.weierstrass_p(prec=6, algorithm='fast')
z^-2 + 2*z^2 + 3*z^4 + O(z^6)
sage: E.weierstrass_p(prec=7, algorithm='fast')
...
ValueError: For computing the Weierstrass p-function via the fast algorithm, the characteristic (11) of the underlying field must be greater than prec + 4 = 11.
sage: E.weierstrass_p(prec=8 ,algorithm='pari')
z^-2 + 2*z^2 + 3*z^4 + 5*z^6 + O(z^8)
sage: E.weierstrass_p(prec=9, algorithm='pari')
...
ValueError: For computing the Weierstrass p-function via pari, the characteristic (11) of the underlying field must be greater than prec + 2 = 11.