Modular symbols

To an elliptic curves 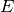over the rational numbers one can associate a space - or better two spaces - of modular symbols of level 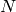, equal to the conductor of 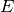; because 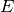is known to be modular.

There are two implementations of modular symbols, one within sage and the other as part of Cremona’s eclib. One can choose here which one is used.

The normalisation of our modular symbols attached to 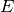can be chosen, too. For instance one can make it depended on 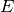rather than on its isogeny class. This is useful for -adic L-functions.

For more details on modular symbols consult the following

REFERENCES:

• [MTT] B. Mazur, J. Tate, and J. Teitelbaum, On -adic analogues of the conjectures of Birch and Swinnerton-Dyer, Inventiones mathematicae 84, (1986), 1-48.
• [Cre] John Cremona, Algorithms for modular elliptic curves, Cambridge University Press, 1997.
• [SW] William Stein and Christian Wuthrich, Computations About Tate-Shafarevich Groups using Iwasawa theory, preprint 2009.

AUTHORS:

• William Stein (2007): first version
• Chris Wuthrich (2008): add scaling and reference to eclib

class sage.schemes.elliptic_curves.ell_modular_symbols.ModularSymbol

Bases: sage.structure.sage_object.SageObject

A modular symbol attached to an elliptic curve, which is the map 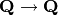obtained by sending to the normalized symmetrized (or anti-symmetrized) integral from to .

This is as defined in [MTT], but normalized to depend on the curve and not only its isogeny class as in [SW].

See the documentation of E.modular_symbol() in Elliptic curves over the rational numbers for help.

REFERENCES:

• [MTT] B. Mazur, J. Tate, and J. Teitelbaum, On -adic analogues of the conjectures of Birch and Swinnerton-Dyer, Inventiones mathematicae 84, (1986), 1-48.
• [SW] William Stein and Christian Wuthrich, Computations About Tate-Shafarevich Groups using Iwasawa theory, preprint 2009.

base_ring()

Return the base ring for this modular symbol.

EXAMPLES:

sage: m = EllipticCurve('11a1').modular_symbol()
sage: m.base_ring()
Rational Field

elliptic_curve()

Return the elliptic curve of this modular symbol.

EXAMPLES:

sage: m = EllipticCurve('11a1').modular_symbol()
sage: m.elliptic_curve()
Elliptic Curve defined by y^2 + y = x^3 - x^2 - 10*x - 20 over Rational Field

sign()

Return the sign of this elliptic curve modular symbol.

EXAMPLES:

sage: m = EllipticCurve('11a1').modular_symbol()
sage: m.sign()
1
sage: m = EllipticCurve('11a1').modular_symbol(sign=-1)
sage: m.sign()
-1

class sage.schemes.elliptic_curves.ell_modular_symbols.ModularSymbolECLIB(E, sign, normalize='L_ratio')

Bases: sage.schemes.elliptic_curves.ell_modular_symbols.ModularSymbol

class sage.schemes.elliptic_curves.ell_modular_symbols.ModularSymbolSage(E, sign, normalize='L_ratio')

Bases: sage.schemes.elliptic_curves.ell_modular_symbols.ModularSymbol

sage.schemes.elliptic_curves.ell_modular_symbols.modular_symbol_space(E, sign, base_ring, bound=None)

Creates the space of modular symbols of a given sign over a give base_ring, attached to the isogeny class of elliptic curves.

INPUT:

• E - an elliptic curve over
• sign - integer, -1, 0, or 1
• base_ring - ring
• bound - (default: None) maximum number of Hecke operators to use to cut out modular symbols factor. If None, use enough to provably get the correct answer.

OUTPUT: a space of modular symbols

EXAMPLES:

sage: import sage.schemes.elliptic_curves.ell_modular_symbols
sage: E=EllipticCurve('11a1')
sage: M=sage.schemes.elliptic_curves.ell_modular_symbols.modular_symbol_space(E,-1,GF(37))
sage: M
Modular Symbols space of dimension 1 for Gamma_0(11) of weight 2 with sign -1 over Finite Field of size 37