Kodaira symbols.

Kodaira symbols encode the type of reduction of an elliptic curve at a (finite) place.

The standard notation for Kodaira Symbols is as a string which is one of 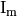, , 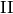, , 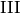, , 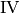, , 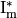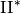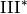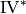where denotes a non-negative integer. These have been encoded by single integers by different people. For convenience we give here the conversion table between strings, the eclib coding and the pari encoding.

Kodaira Symbol	Eclib coding	Pari Coding

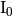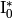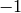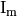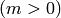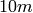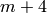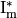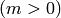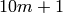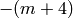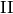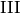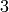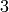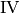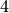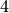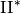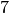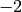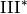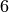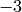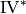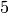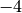AUTHORS:

• David Roe <roed@math.harvard.edu>
• John Cremona

sage.schemes.elliptic_curves.kodaira_symbol.KodairaSymbol(symbol)

Returns the specified Kodaira symbol.

INPUT:

• symbol (string or integer) – Either a string of the form “I0”, “I1”, ..., “In”, “II”, “III”, “IV”, “I0*”, “I1*”, ..., “In*”, “II*”, “III*”, or “IV*”, or an integer encoding a Kodaira symbol using Pari’s conventions.

OUTPUT:

(KodairaSymbol) The corresponding Kodaira symbol.

EXAMPLES:

sage: KS = KodairaSymbol
sage: [KS(n) for n in range(1,10)]
[I0, II, III, IV, I1, I2, I3, I4, I5]
sage: [KS(-n) for n in range(1,10)]
[I0*, II*, III*, IV*, I1*, I2*, I3*, I4*, I5*]
sage: all([KS(str(KS(n)))==KS(n) for n in range(-10,10) if n!=0])
True

class sage.schemes.elliptic_curves.kodaira_symbol.KodairaSymbol_class(symbol)

Bases: sage.structure.sage_object.SageObject

Class to hold a Kodaira symbol of an elliptic curve over a -adic local field.

Users should use the KodairaSymbol() function to construct Kodaira Symbols rather than use the class constructor directly.