Isomorphisms between Weierstrass models of elliptic curves

AUTHORS:

• Robert Bradshaw (2007): initial version
• John Cremona (Jan 2008): isomorphisms, automorphisms and twists in all characteristics

class sage.schemes.elliptic_curves.weierstrass_morphism.WeierstrassIsomorphism(E=None, urst=None, F=None)

Bases: sage.schemes.elliptic_curves.weierstrass_morphism.baseWI, sage.categories.morphism.Morphism

Class representing a Weierstrass isomorphism between two elliptic curves.

class sage.schemes.elliptic_curves.weierstrass_morphism.baseWI(u=1, r=0, s=0, t=0)

This class implements the basic arithmetic of isomorphisms between Weierstrass models of elliptic curves. These are specified by lists of the form (with 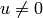) which specifies a transformation 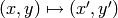where

INPUT:

• u,r,s,t (default (1,0,0,0)) – standard parameters of an isomorphism between Weierstrass models.

EXAMPLES:

sage: from sage.schemes.elliptic_curves.weierstrass_morphism import *
sage: baseWI()
(1, 0, 0, 0)
sage: baseWI(2,3,4,5)
(2, 3, 4, 5)
sage: R.<u,r,s,t>=QQ[]; baseWI(u,r,s,t)
(u, r, s, t)

is_identity()

Returns True if this is the identity isomorphism.

EXAMPLES:

sage: from sage.schemes.elliptic_curves.weierstrass_morphism import *
sage: w=baseWI(); w.is_identity()
True
sage: w=baseWI(2,3,4,5); w.is_identity()
False

tuple()

Returns the parameters 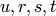as a tuple.

EXAMPLES:

sage: from sage.schemes.elliptic_curves.weierstrass_morphism import *
sage: u,r,s,t=baseWI(2,3,4,5).tuple()
sage: w=baseWI(2,3,4,5)
sage: u,r,s,t=w.tuple()
sage: u
2

sage.schemes.elliptic_curves.weierstrass_morphism.isomorphisms(E, F, JustOne=False)

Returns one or all isomorphisms between two elliptic curves.

INPUT:

• E, F (EllipticCurve) – Two elliptic curves.
• JustOne (bool) If True, returns one isomorphism, or None if the curves are not isomorphic. If False, returns a (possibly empty) list of isomorphisms.

OUTPUT:

Either None, or a 4-tupl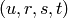e representing an isomorphism, or a list of these.

Note

This function is not intended for users, who should use the interface provided by ell_generic.

EXAMPLES:

sage: from sage.schemes.elliptic_curves.weierstrass_morphism import *
sage: isomorphisms(EllipticCurve_from_j(0),EllipticCurve('27a3'))
[(-1, 0, 0, -1), (1, 0, 0, 0)]
sage: isomorphisms(EllipticCurve_from_j(0),EllipticCurve('27a3'),JustOne=True)
(1, 0, 0, 0)
sage: isomorphisms(EllipticCurve_from_j(0),EllipticCurve('27a1'))
[]
sage: isomorphisms(EllipticCurve_from_j(0),EllipticCurve('27a1'),JustOne=True)