Local data for elliptic curves over number fields

Let be an elliptic curve over a number field (including ). There are several local invariants at a finite place that can be computed via Tate’s algorithm (see [Sil2] IV.9.4 or [Ta]).

These include the type of reduction (good, additive, multiplicative), a minimal equation of over 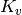, the Tamagawa number 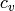, defined to be the index of the points with good reduction among the local points, and the exponent of the conductor .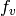

The functions in this file will typically be called by using local_data.

EXAMPLES:

sage: K.<i> = NumberField(x^2+1)
sage: E = EllipticCurve([(2+i)^2,(2+i)^7])
sage: pp = K.fractional_ideal(2+i)
sage: da = E.local_data(pp)
sage: da.has_bad_reduction()
True
sage: da.has_multiplicative_reduction()
False
sage: da.kodaira_symbol()
I0*
sage: da.tamagawa_number()
4
sage: da.minimal_model()
Elliptic Curve defined by y^2 = x^3 + (4*i+3)*x + (-29*i-278) over Number Field in i with defining polynomial x^2 + 1

An example to show how the Neron model can change as one extends the field:

sage: E = EllipticCurve([0,-1])
sage: E.local_data(2)
Local data at Principal ideal (2) of Integer Ring:
Reduction type: bad additive
Local minimal model: Elliptic Curve defined by y^2 = x^3 - 1 over Rational Field
Minimal discriminant valuation: 4
Conductor exponent: 4
Kodaira Symbol: II
Tamagawa Number: 1

sage: EK = E.base_extend(K)
sage: EK.local_data(1+i)
Local data at Fractional ideal (i + 1):
Reduction type: bad additive
Local minimal model: Elliptic Curve defined by y^2 = x^3 + (-1) over Number Field in i with defining polynomial x^2 + 1
Minimal discriminant valuation: 8
Conductor exponent: 2
Kodaira Symbol: IV*
Tamagawa Number: 3

Or how the minimal equation changes:

sage: E = EllipticCurve([0,8])
sage: E.is_minimal()
True
sage: EK = E.base_extend(K)
sage: da = EK.local_data(1+i)
sage: da.minimal_model()
Elliptic Curve defined by y^2 = x^3 + i over Number Field in i with defining polynomial x^2 + 1

REFERENCES:

• [Sil2] Silverman, Joseph H., Advanced topics in the arithmetic of elliptic curves. Graduate Texts in Mathematics, 151. Springer-Verlag, New York, 1994.
• [Ta] Tate, John, Algorithm for determining the type of a singular fiber in an elliptic pencil. Modular functions of one variable, IV, pp. 33–52. Lecture Notes in Math., Vol. 476, Springer, Berlin, 1975.

AUTHORS:

• John Cremona: First version 2008-09-21 (refactoring code from ell_number_field.py and ell_rational_field.py)
• Chris Wuthrich: more documentation 2010-01

class sage.schemes.elliptic_curves.ell_local_data.EllipticCurveLocalData(E, P, proof=None, algorithm='pari')

Bases: sage.structure.sage_object.SageObject

The class for the local reduction data of an elliptic curve.

Currently supported are elliptic curves defined over , and elliptic curves defined over a number field, at an arbitrary prime or prime ideal.

INPUT:

• E – an elliptic curve defined over a number field, or .
• P – a prime ideal of the field, or a prime integer if the field is .
• proof (bool)– if True, only use provably correct methods (default controlled by global proof module). Note that the proof module is number_field, not elliptic_curves, since the functions that actually need the flag are in number fields.
• algorithm (string, default: “pari”) – Ignored unless the base field is . If “pari”, use the PARI C-library ellglobalred implementation of Tate’s algorithm over . If “generic”, use the general number field implementation.

Note

This function is not normally called directly by users, who may access the data via methods of the EllipticCurve classes.

EXAMPLES:

sage: from sage.schemes.elliptic_curves.ell_local_data import EllipticCurveLocalData
sage: E = EllipticCurve('14a1')
sage: EllipticCurveLocalData(E,2)
Local data at Principal ideal (2) of Integer Ring:
Reduction type: bad non-split multiplicative
Local minimal model: Elliptic Curve defined by y^2 + x*y + y = x^3 + 4*x - 6 over Rational Field
Minimal discriminant valuation: 6
Conductor exponent: 1
Kodaira Symbol: I6
Tamagawa Number: 2

bad_reduction_type()

Return the type of bad reduction of this reduction data.

OUTPUT:

(int or None):

• +1 for split multiplicative reduction
• -1 for non-split multiplicative reduction
• 0 for additive reduction
• None for good reduction

EXAMPLES:

sage: E=EllipticCurve('14a1')
sage: [(p,E.local_data(p).bad_reduction_type()) for p in prime_range(15)]
[(2, -1), (3, None), (5, None), (7, 1), (11, None), (13, None)]

sage: K.<a>=NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.local_data(p).bad_reduction_type()) for p in [P17a,P17b]]           
[(Fractional ideal (4*a^2 - 2*a + 1), None), (Fractional ideal (2*a + 1), 0)]

conductor_valuation()

Return the valuation of the conductor from this local reduction data.

EXAMPLES:

sage: from sage.schemes.elliptic_curves.ell_local_data import EllipticCurveLocalData
sage: E = EllipticCurve([0,0,0,0,64]); E
Elliptic Curve defined by y^2 = x^3 + 64 over Rational Field
sage: data = EllipticCurveLocalData(E,2)
sage: data.conductor_valuation()
2

has_additive_reduction()

Return True if there is additive reduction.

EXAMPLES:

sage: E = EllipticCurve('27a1')
sage: [(p,E.local_data(p).has_additive_reduction()) for p in prime_range(15)]
[(2, False), (3, True), (5, False), (7, False), (11, False), (13, False)]

sage: K.<a> = NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.local_data(p).has_additive_reduction()) for p in [P17a,P17b]]           
[(Fractional ideal (4*a^2 - 2*a + 1), False),
(Fractional ideal (2*a + 1), True)]

has_bad_reduction()

Return True if there is bad reduction.

EXAMPLES:

sage: E = EllipticCurve('14a1')
sage: [(p,E.local_data(p).has_bad_reduction()) for p in prime_range(15)]
[(2, True), (3, False), (5, False), (7, True), (11, False), (13, False)]

sage: K.<a> = NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.local_data(p).has_bad_reduction()) for p in [P17a,P17b]]           
[(Fractional ideal (4*a^2 - 2*a + 1), False),
(Fractional ideal (2*a + 1), True)]

has_good_reduction()

Return True if there is good reduction.

EXAMPLES:

sage: E = EllipticCurve('14a1')
sage: [(p,E.local_data(p).has_good_reduction()) for p in prime_range(15)]
[(2, False), (3, True), (5, True), (7, False), (11, True), (13, True)]

sage: K.<a> = NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.local_data(p).has_good_reduction()) for p in [P17a,P17b]]           
[(Fractional ideal (4*a^2 - 2*a + 1), True),
(Fractional ideal (2*a + 1), False)]

has_multiplicative_reduction()

Return True if there is multiplicative reduction.

Note

See also has_split_multiplicative_reduction() and has_nonsplit_multiplicative_reduction().

EXAMPLES:

sage: E = EllipticCurve('14a1')
sage: [(p,E.local_data(p).has_multiplicative_reduction()) for p in prime_range(15)]
[(2, True), (3, False), (5, False), (7, True), (11, False), (13, False)]

sage: K.<a> = NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.local_data(p).has_multiplicative_reduction()) for p in [P17a,P17b]]           
[(Fractional ideal (4*a^2 - 2*a + 1), False), (Fractional ideal (2*a + 1), False)]

has_nonsplit_multiplicative_reduction()

Return True if there is non-split multiplicative reduction.

EXAMPLES:

sage: E = EllipticCurve('14a1')
sage: [(p,E.local_data(p).has_nonsplit_multiplicative_reduction()) for p in prime_range(15)]
[(2, True), (3, False), (5, False), (7, False), (11, False), (13, False)]

sage: K.<a> = NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.local_data(p).has_nonsplit_multiplicative_reduction()) for p in [P17a,P17b]]           
[(Fractional ideal (4*a^2 - 2*a + 1), False), (Fractional ideal (2*a + 1), False)]

has_split_multiplicative_reduction()

Return True if there is split multiplicative reduction.

EXAMPLES:

sage: E = EllipticCurve('14a1')
sage: [(p,E.local_data(p).has_split_multiplicative_reduction()) for p in prime_range(15)]
[(2, False), (3, False), (5, False), (7, True), (11, False), (13, False)]

sage: K.<a> = NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.local_data(p).has_split_multiplicative_reduction()) for p in [P17a,P17b]]           
[(Fractional ideal (4*a^2 - 2*a + 1), False),
(Fractional ideal (2*a + 1), False)]

kodaira_symbol()

Return the Kodaira symbol from this local reduction data.

EXAMPLES:

sage: from sage.schemes.elliptic_curves.ell_local_data import EllipticCurveLocalData
sage: E = EllipticCurve([0,0,0,0,64]); E
Elliptic Curve defined by y^2 = x^3 + 64 over Rational Field
sage: data = EllipticCurveLocalData(E,2)
sage: data.kodaira_symbol()
IV

minimal_model()

Return the (local) minimal model from this local reduction data.

EXAMPLES:

sage: from sage.schemes.elliptic_curves.ell_local_data import EllipticCurveLocalData
sage: E = EllipticCurve([0,0,0,0,64]); E
Elliptic Curve defined by y^2  = x^3 + 64 over Rational Field
sage: data = EllipticCurveLocalData(E,2)
sage: data.minimal_model()
Elliptic Curve defined by y^2 = x^3 + 1 over Rational Field
sage: data.minimal_model() == E.local_minimal_model(2)
True

prime()

Return the prime ideal associated with this local reduction data.

EXAMPLES:

sage: from sage.schemes.elliptic_curves.ell_local_data import EllipticCurveLocalData
sage: E = EllipticCurve([0,0,0,0,64]); E
Elliptic Curve defined by y^2 = x^3 + 64 over Rational Field
sage: data = EllipticCurveLocalData(E,2)
sage: data.prime()
Principal ideal (2) of Integer Ring

tamagawa_exponent()

Return the Tamagawa index from this local reduction data.

This is the exponent of 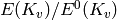; in most cases it is the same as the Tamagawa index.

EXAMPLES:

sage: from sage.schemes.elliptic_curves.ell_local_data import EllipticCurveLocalData
sage: E = EllipticCurve('816a1')
sage: data = EllipticCurveLocalData(E,2)
sage: data.kodaira_symbol()
I2*
sage: data.tamagawa_number()
4
sage: data.tamagawa_exponent()
2

sage: E = EllipticCurve('200c4')
sage: data = EllipticCurveLocalData(E,5)
sage: data.kodaira_symbol()
I4*
sage: data.tamagawa_number()
4
sage: data.tamagawa_exponent()
2

tamagawa_number()

Return the Tamagawa number from this local reduction data.

This is the index .

EXAMPLES:

sage: from sage.schemes.elliptic_curves.ell_local_data import EllipticCurveLocalData
sage: E = EllipticCurve([0,0,0,0,64]); E
Elliptic Curve defined by y^2 = x^3 + 64 over Rational Field
sage: data = EllipticCurveLocalData(E,2)
sage: data.tamagawa_number()
3

sage.schemes.elliptic_curves.ell_local_data.check_prime(K, P)

Function to check that determines a prime of , and return that ideal.

INPUT:

• K – a number field (including ).
• P – an element of K or a (fractional) ideal of K.

OUTPUT:

• If K is : the prime integer equal to or which generates .
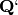• If K is not : the prime ideal equal to or generated by .

Note

If is not a prime and does not generate a prime, a TypeError is raised.

EXAMPLES:

sage: from sage.schemes.elliptic_curves.ell_local_data import check_prime
sage: check_prime(QQ,3)
3
sage: check_prime(QQ,ZZ.ideal(31))
31
sage: K.<a>=NumberField(x^2-5)
sage: check_prime(K,a)
Fractional ideal (a)
sage: check_prime(K,a+1)
Fractional ideal (a + 1)
sage: [check_prime(K,P) for P in K.primes_above(31)]
[Fractional ideal (-5/2*a - 1/2), Fractional ideal (-5/2*a + 1/2)]