If  is an elliptic curve over a global field
is an elliptic curve over a global field  , currently only implemented over
, currently only implemented over  .
.
Given an elliptic curve  over a number field
over a number field  and a rational prime number
and a rational prime number  , the
, the  -torsion
-torsion
![E[p^n]](../../../_images/math/17578c5290e70ffbae76bd91d2ca2d6dfee7fd55.png) points of
points of  is a representation of the
absolute Galois group
is a representation of the
absolute Galois group 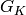 of
of  . As
. As  varies
we obtain the Tate module
varies
we obtain the Tate module 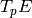 which is a
a representation of
which is a
a representation of 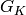 on a free
on a free 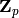 -module
of rank
-module
of rank  . As
. As  varies the representations
are compatible.
varies the representations
are compatible.
Currently sage can decide whether the Galois module
![E[p]](../../../_images/math/5d889bb1b1427121620fc76b1ce4441abd1c078c.png) is reducible, i.e. if
is reducible, i.e. if  admits an isogeny
of degree
admits an isogeny
of degree  , and whether the image of
the representation on
, and whether the image of
the representation on ![E[p]](../../../_images/math/5d889bb1b1427121620fc76b1ce4441abd1c078c.png) is surjective onto
is surjective onto
![Aut(E[p]) = GL_2(\mathbb{F}_p)](../../../_images/math/4e9435c7bb8c8cd9aa08395066aabba5d7ab037a.png) .
.
EXAMPLES:
sage: E = EllipticCurve('196a1')
sage: rho = E.galois_representation()
sage: rho.is_irreducible(7)
True
sage: rho.is_reducible(3)
True
sage: rho.is_irreducible(2)
True
sage: rho.is_surjective(2)
False
sage: rho.is_surjective(3)
False
sage: rho.is_surjective(5)
True
sage: rho.reducible_primes()
[3]
sage: rho.non_surjective()
[2, 3]
For semi-stable curve it is known that the representation is surjective if and only if it is irreducible:
sage: E = EllipticCurve('11a1')
sage: rho = E.galois_representation()
sage: rho.non_surjective()
[5]
sage: rho.reducible_primes()
[5]
For cm curves it is not true that there are only finitely many primes for which the
Galois representation mod p is surjective onto 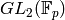 :
:
sage: E = EllipticCurve('27a1')
sage: rho = E.galois_representation()
sage: rho.non_surjective()
[0]
sage: rho.reducible_primes()
[3]
sage: E.has_cm()
True
REFERENCES:
| [Se1] | Jean-Pierre Serre, Propriétés galoisiennes des points d’ordre fini des courbes elliptiques. Invent. Math. 15 (1972), no. 4, 259–331. |
| [Se2] | Jean-Pierre Serre, Sur les représentations modulaires de degré 2 de Gal`(overlineQQ/QQ)`. Duke Math. J. 54 (1987), no. 1, 179–230. |
| [Co] | Alina Carmen Cojocaru, On the surjectivity of the Galois representations associated to non-CM elliptic curves. With an appendix by Ernst Kani. Canad. Math. Bull. 48 (2005), no. 1, 16–31. |
AUTHORS:
Bases: sage.structure.sage_object.SageObject
The compatible family of Galois representation attached to an elliptic curve over a number field.
Given an elliptic curve  over a number field
over a number field  and a rational prime number
and a rational prime number  , the
, the  -torsion
-torsion
![E[p^n]](../../../_images/math/17578c5290e70ffbae76bd91d2ca2d6dfee7fd55.png) points of
points of  is a representation of the
absolute Galois group
is a representation of the
absolute Galois group 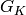 of
of  . As
. As  varies
we obtain the Tate module
varies
we obtain the Tate module 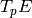 which is a
a representation of
which is a
a representation of 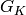 on a free
on a free 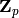 -module
of rank
-module
of rank  . As
. As  varies the representations
are compatible.
varies the representations
are compatible.
EXAMPLES:
sage: rho = EllipticCurve('11a1').galois_representation()
sage: rho
Compatible family of Galois representations associated to the Elliptic Curve defined by y^2 + y = x^3 - x^2 - 10*x - 20 over Rational Field
The elliptic curve associated to this representation.
EXAMPLES:
sage: E = EllipticCurve('11a1')
sage: rho = E.galois_representation()
sage: rho.elliptic_curve() == E
True
Return True if the mod p representation is irreducible.
EXAMPLES:
sage: rho = EllipticCurve('37b').galois_representation()
sage: rho.is_irreducible(2)
True
sage: rho.is_irreducible(3)
False
sage: rho.is_reducible(2)
False
sage: rho.is_reducible(3)
True
Return True if the mod-p representation is
reducible. This is equivalent to the existence of an
isogeny of degree  from the elliptic curve.
from the elliptic curve.
INPUT:
Note
The answer is cached.
EXAMPLES:
sage: rho = EllipticCurve('121a').galois_representation()
sage: rho.is_reducible(7)
False
sage: rho.is_reducible(11)
True
sage: EllipticCurve('11a').galois_representation().is_reducible(5)
True
sage: rho = EllipticCurve('11a2').galois_representation()
sage: rho.is_reducible(5)
True
sage: EllipticCurve('11a2').torsion_order()
1
Return True if the mod-p representation is
surjective onto ![Aut(E[p]) = GL_2(\mathbb{F}_p)](../../../_images/math/4e9435c7bb8c8cd9aa08395066aabba5d7ab037a.png) .
.
False if it is not, or None if we were unable to determine whether it is or not.
Note
The answer is cached.
INPUT:
OUTPUT:
EXAMPLES:
sage: rho = EllipticCurve('37b').galois_representation()
sage: rho.is_surjective(2)
True
sage: rho.is_surjective(3)
False
REMARKS:
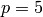 then the mod-p representation is
surjective if and only if the p-adic representation is
surjective. When
then the mod-p representation is
surjective if and only if the p-adic representation is
surjective. When 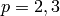 there are
counterexamples. See a very recent paper of Elkies for more
details when
there are
counterexamples. See a very recent paper of Elkies for more
details when 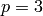 .
.Returns a list of primes p such that the mod-p representation
might not be surjective (this list
usually contains 2, because of shortcomings of the algorithm). If  is not in the returned list, then the mod-p representation
is provably surjective.
is not in the returned list, then the mod-p representation
is provably surjective.
By a theorem of Serre, there are only finitely many primes in this list, except when the curve has complex multiplication.
If the curve has CM, we simply return the sequence [0] and do no further computation.
INPUT:
OUTPUT:
EXAMPLES:
sage: E = EllipticCurve([0, 0, 1, -38, 90]) # 361A
sage: E.galois_representation().non_surjective() # CM curve
[0]
sage: E = EllipticCurve([0, -1, 1, 0, 0]) # X_1(11)
sage: E.galois_representation().non_surjective()
[5]
sage: E = EllipticCurve([0, 0, 1, -1, 0]) # 37A
sage: E.galois_representation().non_surjective()
[]
sage: E = EllipticCurve([0,-1,1,-2,-1]) # 141C
sage: E.galois_representation().non_surjective()
[13]
ALGORITHM: When 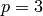 use division polynomials.
For
use division polynomials.
For 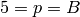 , where
, where
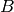 is Cojocaru’s bound, use the results in Section 2 of
is Cojocaru’s bound, use the results in Section 2 of
Returns a list of the primes  such that the mod
such that the mod
 representation is reducible. For
all other primes the representation is irreducible.
representation is reducible. For
all other primes the representation is irreducible.
EXAMPLES:
sage: rho = EllipticCurve('225a').galois_representation()
sage: rho.reducible_primes()
[3]