If  is an elliptic curve over a global field
is an elliptic curve over a global field  , the Shafarevich-Tate group
is the subgroup of elements in
, the Shafarevich-Tate group
is the subgroup of elements in 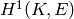 which map to zero under every global-to-local
restriction map
which map to zero under every global-to-local
restriction map 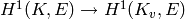 , one for each place
, one for each place  of
of  . It is known to be a torsion group and the
. It is known to be a torsion group and the 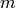 -torsion is finite for all
-torsion is finite for all 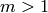 .
It is conjectured to be finite.
.
It is conjectured to be finite.
AUTHORS:
Bases: sage.structure.sage_object.SageObject
The Shafarevich-Tate group associated to an elliptic curve.
If  is an elliptic curve over a global field
is an elliptic curve over a global field  , the Shafarevich-Tate group
is the subgroup of elements in
, the Shafarevich-Tate group
is the subgroup of elements in 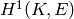 which map to zero under every global-to-local
restriction map
which map to zero under every global-to-local
restriction map 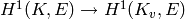 , one for each place
, one for each place  of
of  .
.
EXAMPLES:
sage: E = EllipticCurve('389a')
sage: E.sha()
Shafarevich-Tate group for the Elliptic Curve defined by y^2 + y = x^3 + x^2 - 2*x over Rational Field
Returns the Birch and Swinnerton-Dyer conjectural order of Sha as a provably correct integer, unless the analytic rank is > 1, in which case this function returns a numerical value.
INPUT:
- use_database – bool (default: False); if True, try to use any databases installed to lookup the analytic order of Sha, if possible. The order of Sha is computed if it can’t be looked up.
- descent_second_limit – int (default: 12); limit to use on point searching for the quartic twist in the hard case
This result is proved correct if the order of vanishing is 0 and the Manin constant is <= 2.
If the optional parameter use_database is True (default: False), this function returns the analytic order of Sha as listed in Cremona’s tables, if this curve appears in Cremona’s tables.
NOTE:
If you come across the following error:
sage: E = EllipticCurve([0, 0, 1, -34874, -2506691])
sage: E.sha().an()
...
RuntimeError: Unable to compute the rank, hence generators, with certainty (lower bound=0, generators found=[]). This could be because Sha(E/Q)[2] is nontrivial.
Try increasing descent_second_limit then trying this command again.
You can increase the 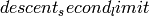 (in the above example,
set to the default, 12) option to try again:
(in the above example,
set to the default, 12) option to try again:
sage: E.sha().an(descent_second_limit=16)
1
EXAMPLES:
sage: E = EllipticCurve([0, -1, 1, -10, -20]) # 11A = X_0(11)
sage: E.sha().an()
1
sage: E = EllipticCurve([0, -1, 1, 0, 0]) # X_1(11)
sage: E.sha().an()
1
sage: EllipticCurve('14a4').sha().an()
1
sage: EllipticCurve('14a4').sha().an(use_database=True) # will be faster if you have large Cremona database installed
1
The smallest conductor curve with nontrivial Sha:
sage: E = EllipticCurve([1,1,1,-352,-2689]) # 66b3
sage: E.sha().an()
4
The four optimal quotients with nontrivial Sha and conductor <= 1000:
sage: E = EllipticCurve([0, -1, 1, -929, -10595]) # 571A
sage: E.sha().an()
4
sage: E = EllipticCurve([1, 1, 0, -1154, -15345]) # 681B
sage: E.sha().an()
9
sage: E = EllipticCurve([0, -1, 0, -900, -10098]) # 960D
sage: E.sha().an()
4
sage: E = EllipticCurve([0, 1, 0, -20, -42]) # 960N
sage: E.sha().an()
4
The smallest conductor curve of rank > 1:
sage: E = EllipticCurve([0, 1, 1, -2, 0]) # 389A (rank 2)
sage: E.sha().an()
1.00000000000000
The following are examples that require computation of the Mordell-Weil group and regulator:
sage: E = EllipticCurve([0, 0, 1, -1, 0]) # 37A (rank 1)
sage: E.sha().an()
1
sage: E = EllipticCurve("1610f3")
sage: E.sha().an()
4
In this case the input curve is not minimal, and if this function didn’t transform it to be minimal, it would give nonsense:
sage: E = EllipticCurve([0,-432*6^2])
sage: E.sha().an()
1
Return the numerical analytic order of Sha, which is a floating point number in all cases.
INPUT:
Note
See also the an() command, which will return a provably correct integer when the rank is 0 or 1.
Warning
If the curve’s generators are not known, computing them may be very time-consuming. Also, computation of the L-series derivative will be time-consuming for large rank and large conductor, and the computation time for this may increase substantially at greater precision. However, use of very low precision less than about 10 can cause the underlying pari library functions to fail.
EXAMPLES:
sage: EllipticCurve('11a').sha().an_numerical()
1.00000000000000
sage: EllipticCurve('37a').sha().an_numerical() # long time
1.00000000000000
sage: EllipticCurve('389a').sha().an_numerical() # long time
1.00000000000000
sage: EllipticCurve('66b3').sha().an_numerical()
4.00000000000000
sage: EllipticCurve('5077a').sha().an_numerical() # long time
1.00000000000000
A rank 4 curve:
sage: EllipticCurve([1, -1, 0, -79, 289]).sha().an_numerical() # long time
1.00000000000000
A rank 5 curve:
sage: EllipticCurve([0, 0, 1, -79, 342]).sha().an_numerical(prec=10, proof=False) # long time -- about 30 seconds.
1.0
# See trac #1115
sage: sha=EllipticCurve('37a1').sha()
sage: [sha.an_numerical(prec) for prec in xrange(40,100,10)] # long time
[1.0000000000,
1.0000000000000,
1.0000000000000000,
1.0000000000000000000,
1.0000000000000000000000,
1.0000000000000000000000000]
Returns the conjectural order of Sha(E),
according to the  -adic analogue of the Birch
and Swinnerton-Dyer conjecture as formulated
in [MTT] and [BP].
-adic analogue of the Birch
and Swinnerton-Dyer conjecture as formulated
in [MTT] and [BP].
REFERENCES:
 -adic analogues of the conjectures of Birch and
Swinnerton-Dyer, Inventiones mathematicae 84, (1986), 1-48.
-adic analogues of the conjectures of Birch and
Swinnerton-Dyer, Inventiones mathematicae 84, (1986), 1-48. -adique de la conjecture de Birch et
Swinnerton-Dyer (le cas supersingulier), C. R. Acad. Sci. Paris,
Ser I. Math, 317 (1993), no 3, 227-232.
-adique de la conjecture de Birch et
Swinnerton-Dyer (le cas supersingulier), C. R. Acad. Sci. Paris,
Ser I. Math, 317 (1993), no 3, 227-232.INPUT:
 -adic L-Series
-adic L-SeriesOUTPUT:  -adic number - that conjecturally equals
-adic number - that conjecturally equals  .
.
If prec is set to zero (default) then the precision is set so that
at least the first  -adic digit of conjectural
-adic digit of conjectural  is
determined.
is
determined.
EXAMPLES: Good ordinary examples:
sage: EllipticCurve('11a1').sha().an_padic(5) #rank 0
1 + O(5^2)
sage: EllipticCurve('43a1').sha().an_padic(5) #rank 1
1 + O(5)
sage: EllipticCurve('389a1').sha().an_padic(5,4) #rank 2 (long time)
1 + O(5^3)
sage: EllipticCurve('858k2').sha().an_padic(7) #rank 0, non trivial sha (long time)
7^2 + O(7^6)
sage: EllipticCurve('300b2').sha().an_padic(3) # an example with 9 elements in sha
3^2 + O(3^6)
sage: EllipticCurve('300b2').sha().an_padic(7, prec=6)
2 + 7 + O(7^8)
Exceptional cases:
sage: EllipticCurve('11a1').sha().an_padic(11) #rank 0
1 + O(11^2)
sage: EllipticCurve('130a1').sha().an_padic(5) #rank 1
1 + O(5)
Non-split, but rank 0 case (trac #7331):
sage: EllipticCurve('270b1').sha().an_padic(5) #rank 0
1 + O(5^2)
The output has the correct sign
sage: EllipticCurve('123a1').sha().an_padic(41) #rank 1 (long time)
1 + O(41)
Supersingular cases:
sage: EllipticCurve('34a1').sha().an_padic(5) # rank 0
1 + O(5^2)
sage: EllipticCurve('53a1').sha().an_padic(5) # rank 1 (long time)
1 + O(5)
Cases that use a twist to a lower conductor
sage: EllipticCurve('99a1').sha().an_padic(5)
1 + O(5)
sage: EllipticCurve('240d3').sha().an_padic(5) # sha has 4 elements here
4 + O(5)
sage: EllipticCurve('448c5').sha().an_padic(7,prec=4, use_twists=False)
2 + 7 + O(7^6)
sage: E = EllipticCurve([-19,34]) # trac 6455
sage: E.sha().an_padic(5) # long time
1 + O(5)
Compute a provably correct bound on the order of the Shafarevich-Tate group of this curve. The bound is a either False (no bound) or a list B of primes such that any divisor of Sha is in this list.
EXAMPLES:
sage: EllipticCurve('37a').sha().bound()
([2], 1)
Returns a list  of primes such that the theorems of Kato’s [Ka]
and others (e.g., as explained in a paper/thesis of Grigor
Grigorov [Gri]) imply that if
of primes such that the theorems of Kato’s [Ka]
and others (e.g., as explained in a paper/thesis of Grigor
Grigorov [Gri]) imply that if  divides the order of Sha(E) then
divides the order of Sha(E) then  is in
the list.
is in
the list.
If 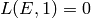 , then this function gives no information, so
it returns False.
, then this function gives no information, so
it returns False.
THEOREM (Kato): Suppose  and
and 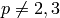 is a prime such that
is a prime such that
does not have additive reduction at
,
- the mod-
representation is surjective.
Then 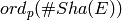 divides
divides 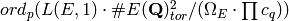 .
.
EXAMPLES:
sage: E = EllipticCurve([0, -1, 1, -10, -20]) # 11A = X_0(11)
sage: E.sha().bound_kato()
[2, 3, 5]
sage: E = EllipticCurve([0, -1, 1, 0, 0]) # X_1(11)
sage: E.sha().bound_kato()
[2, 3, 5]
sage: E = EllipticCurve([1,1,1,-352,-2689]) # 66B3
sage: E.sha().bound_kato()
[2, 3]
For the following curve one really has that 25 divides the order of Sha (by Grigorov-Stein paper [GS]):
sage: E = EllipticCurve([1, -1, 0, -332311, -73733731]) # 1058D1
sage: E.sha().bound_kato() # long time (about 1 second)
[2, 3, 5, 23]
sage: E.galois_representation().non_surjective() # long time (about 1 second)
[]
For this one, Sha is divisible by 7:
sage: E = EllipticCurve([0, 0, 0, -4062871, -3152083138]) # 3364C1
sage: E.sha().bound_kato() # long time (< 10 seconds)
[2, 3, 7, 29]
No information about curves of rank > 0:
sage: E = EllipticCurve([0, 0, 1, -1, 0]) # 37A (rank 1)
sage: E.sha().bound_kato()
False
REFERENCES:
 -adic Hodge theory and values of zeta functions of modular
forms, Cohomologies
-adic Hodge theory and values of zeta functions of modular
forms, Cohomologies  -adiques et applications arithmetiques III,
Asterisque vol 295, SMF, Paris, 2004.
-adiques et applications arithmetiques III,
Asterisque vol 295, SMF, Paris, 2004.Given a fundamental discriminant 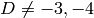 that satisfies the
Heegner hypothesis for
that satisfies the
Heegner hypothesis for  , return a list of primes so that
Kolyvagin’s theorem (as in Gross’s paper) implies that any
prime divisor of Sha is in this list.
, return a list of primes so that
Kolyvagin’s theorem (as in Gross’s paper) implies that any
prime divisor of Sha is in this list.
INPUT:
 ; if not given, use the first such
; if not given, use the first such 
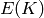 ; if not given, will
be computed (which could take a long time)
; if not given, will
be computed (which could take a long time) representation.
representation.OUTPUT:
 divides Sha(E/K), then
divides Sha(E/K), then
 is in this list, unless
is in this list, unless 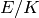 has complex multiplication or
analytic rank greater than 2 (in which case we return 0).
has complex multiplication or
analytic rank greater than 2 (in which case we return 0). -rational points on E. (If
-rational points on E. (If  has CM, returns 0.)
has CM, returns 0.)REMARKS:
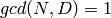 , instead of the stronger
hypothesis
, instead of the stronger
hypothesis 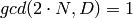 that is in the original
Gross-Zagier paper. That Gross-Zagier is true when
that is in the original
Gross-Zagier paper. That Gross-Zagier is true when
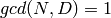 is”well-known” to the experts, but doesn’t
seem to written up well in the literature.
is”well-known” to the experts, but doesn’t
seem to written up well in the literature.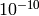 , i.e., they are
correct up to addition or a real number with absolute
value less than
, i.e., they are
correct up to addition or a real number with absolute
value less than 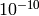 .
.EXAMPLES:
sage: E = EllipticCurve('37a')
sage: E.sha().bound_kolyvagin()
([2], 1)
sage: E = EllipticCurve('141a')
sage: E.sha().an()
1
sage: E.sha().bound_kolyvagin()
([2, 7], 49)
We get no information the curve has rank 2.:
sage: E = EllipticCurve('389a')
sage: E.sha().bound_kolyvagin()
(0, 0)
sage: E = EllipticCurve('681b')
sage: E.sha().an()
9
sage: E.sha().bound_kolyvagin()
([2, 3], 9)
Returns a provable upper bound for the order of  . In particular,
if this algorithm does not fail, then it proves that the
. In particular,
if this algorithm does not fail, then it proves that the  -primary
part of Sha is finite.
-primary
part of Sha is finite.
INPUT: p – a prime > 2
OUTPUT: integer – power of  that bounds the order of
that bounds the order of  from above
from above
The result is a proven upper bound on the order of  .
So in particular it proves it finiteness even if the rank of
the curve is larger than 1. Note also that this bound is sharp
if one assumes the main conjecture of Iwasawa theory of
elliptic curves (and this is known in certain cases).
.
So in particular it proves it finiteness even if the rank of
the curve is larger than 1. Note also that this bound is sharp
if one assumes the main conjecture of Iwasawa theory of
elliptic curves (and this is known in certain cases).
Currently the algorithm is only implemented when certain conditions are verified.
 Galois representation must be surjective.
Galois representation must be surjective. is not allowed to be additive.
is not allowed to be additive. is non-split multiplicative, then the rank has to be 0.
is non-split multiplicative, then the rank has to be 0.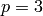 then the reduction at 3 must be good ordinary or split multiplicative and the rank must be 0.
then the reduction at 3 must be good ordinary or split multiplicative and the rank must be 0.EXAMPLES:
sage: e = EllipticCurve('11a3')
sage: e.sha().p_primary_bound(3)
0
sage: e.sha().p_primary_bound(7)
0
sage: e.sha().p_primary_bound(11)
0
sage: e.sha().p_primary_bound(13)
0
sage: e = EllipticCurve('389a1')
sage: e.sha().p_primary_bound(5)
0
sage: e.sha().p_primary_bound(7)
0
sage: e.sha().p_primary_bound(11)
0
sage: e.sha().p_primary_bound(13)
0
sage: e = EllipticCurve('858k2')
sage: e.sha().p_primary_bound(3) # long time
0
# checks for trac 6406
sage: e.sha().p_primary_bound(7)
...
ValueError: The mod-p Galois representation is not surjective. Current knowledge about Euler systems does not provide an upper bound in this case. Try an_padic for a conjectural bound.
sage: e.sha().an_padic(7)
7^2 + O(7^6)
sage: e = EllipticCurve('11a3')
sage: e.sha().p_primary_bound(5)
...
ValueError: The mod-p Galois representation is not surjective. Current knowledge about Euler systems does not provide an upper bound in this case. Try an_padic for a conjectural bound.
sage: e.sha().an_padic(5)
1 + O(5^2)
This returns the 2-rank, i.e. the 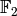 -dimension
of the 2-torsion part of Sha, provided we can determine the
rank of
-dimension
of the 2-torsion part of Sha, provided we can determine the
rank of  .
EXAMPLE:
.
EXAMPLE:
sage: sh = EllipticCurve('571a1').sha()
sage: sh.two_selmer_bound()
2
sage: sh.an()
4
sage: sh = EllipticCurve('66a1').sha()
sage: sh.two_selmer_bound()
0
sage: sh.an()
1
sage: sh = EllipticCurve('960d1').sha()
sage: sh.two_selmer_bound()
2
sage: sh.an()
4