AUTHORS:
Bases: sage.schemes.elliptic_curves.ell_field.EllipticCurve_field, sage.schemes.hyperelliptic_curves.hyperelliptic_finite_field.HyperellipticCurve_finite_field
Elliptic curve over a finite field.
Returns the abelian group structure of the group of points on this elliptic curve.
Warning
The algorithm is definitely not intended for use with
large finite fields! The factorization of the orders of
elements must be feasible. Also, baby-step-giant-step
methods are used which have space and time requirements
which are 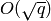 .
.
Also, the algorithm uses random points on the curve and hence the generators are likely to differ from one run to another; but the group is cached so the generators will not change in any one run of Sage.
Note
This function applies to elliptic curves over arbitrary finite fields. The related function abelian_group_prime_field() uses the pari script, for prime fields only; it is now obsolete
INPUT:
OUTPUT:
AUTHORS:
EXAMPLES:
sage: E=EllipticCurve(GF(11),[2,5])
sage: E.abelian_group()
(Multiplicative Abelian Group isomorphic to C10, ...
sage: E=EllipticCurve(GF(41),[2,5])
sage: E.abelian_group()
(Multiplicative Abelian Group isomorphic to C22 x C2, ...
sage: F.<a>=GF(3^6,'a')
sage: E=EllipticCurve([a^4 + a^3 + 2*a^2 + 2*a, 2*a^5 + 2*a^3 + 2*a^2 + 1])
sage: E.abelian_group()
(Multiplicative Abelian Group isomorphic to C26 x C26, ...
sage: F.<a>=GF(101^3,'a')
sage: E=EllipticCurve([2*a^2 + 48*a + 27, 89*a^2 + 76*a + 24])
sage: E.abelian_group()
(Multiplicative Abelian Group isomorphic to C1031352, ...
The group can be trivial:
sage: E=EllipticCurve(GF(2),[0,0,1,1,1])
sage: E.abelian_group()
(Trivial Abelian Group, ())
Of course, there are plenty of points if we extend the field:
sage: E.cardinality(extension_degree=100)
1267650600228231653296516890625
This tests the patch for trac #3111, using 10 primes randomly selected:
sage: E = EllipticCurve('389a')
sage: for p in [5927, 2297, 1571, 1709, 3851, 127, 3253, 5783, 3499, 4817]:
... G = E.change_ring(GF(p)).abelian_group()
sage: for p in prime_range(10000): #long time (~20s)
... if p != 389:
... G=E.change_ring(GF(p)).abelian_group()
This tests that the bug reported in trac #3926 has been fixed:
sage: K.<i> = QuadraticField(-1)
sage: OK = K.ring_of_integers()
sage: P=K.factor(10007)[0][0]
sage: OKmodP = OK.residue_field(P)
sage: E = EllipticCurve([0,0,0,i,i+3])
sage: Emod = E.change_ring(OKmodP); Emod
Elliptic Curve defined by y^2 = x^3 + ibar*x + (ibar+3) over Residue field in ibar of Fractional ideal (10007)
sage: Emod.abelian_group() #random generators
(Multiplicative Abelian Group isomorphic to C50067594 x C2,
((3152*ibar + 7679 : 7330*ibar + 7913 : 1), (8466*ibar + 1770 : 0 : 1)))
Return the number of points on this elliptic curve over an extension field (default: the base field).
INPUT:
algorithm - string (default: ‘heuristic’), used only for point counting over prime fields
- 'heuristic' - use a heuristic to choose between pari, bsgs and sea.
- 'pari' - use the baby step giant step method as implemented in PARI via the C-library function ellap.
- 'sea' - use sea.gp as implemented in PARI by Christophe Doche and Sylvain Duquesne. (‘sea’ stands for ‘Schoof-Elkies-Atkin’.)
- bsgs - use the baby step giant step method as implemented in Sage, with the Cremona - Sutherland version of Mestre’s trick.
- all - (over prime fields only) compute cardinality with all of pari, sea and bsgs; return result if they agree or raise a RuntimeError if they do not.
early_abort - bool (default: False); this is used only by sea. if True, stop early if a small factor of the order is found.
extension_degree - int (default: 1); if the
base field is 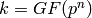 and extension_degree=d, returns
the cardinality of
and extension_degree=d, returns
the cardinality of 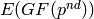 .
.
OUTPUT: an integer
The cardinality is cached.
Over prime fields, one of the above algorithms is used. Over non-prime fields, the serious point counting is done on a standard curve with the same j-invariant over the field GF(p)(j), then lifted to the base_field, and finally account is taken of twists.
For j=0 and j=1728 special formulas are used instead.
EXAMPLES:
sage: EllipticCurve(GF(4,'a'),[1,2,3,4,5]).cardinality()
8
sage: k.<a> = GF(3^3)
sage: l = [a^2 + 1, 2*a^2 + 2*a + 1, a^2 + a + 1, 2, 2*a]
sage: EllipticCurve(k,l).cardinality()
29
sage: l = [1, 1, 0, 2, 0]
sage: EllipticCurve(k,l).cardinality()
38
An even bigger extension (which we check against Magma):
sage: EllipticCurve(GF(3^100,'a'),[1,2,3,4,5]).cardinality()
515377520732011331036459693969645888996929981504
sage: magma.eval("Order(EllipticCurve([GF(3^100)|1,2,3,4,5]))") # optional - magma
'515377520732011331036459693969645888996929981504'
sage: EllipticCurve(GF(10007),[1,2,3,4,5]).cardinality()
10076
sage: EllipticCurve(GF(10007),[1,2,3,4,5]).cardinality(algorithm='sea')
10076
sage: EllipticCurve(GF(10007),[1,2,3,4,5]).cardinality(algorithm='pari')
10076
sage: EllipticCurve(GF(next_prime(10**20)),[1,2,3,4,5]).cardinality(algorithm='sea')
100000000011093199520
The cardinality is cached:
sage: E = EllipticCurve(GF(3^100,'a'),[1,2,3,4,5])
sage: E.cardinality() is E.cardinality()
True
sage: E=EllipticCurve(GF(11^2,'a'),[3,3])
sage: E.cardinality()
128
sage: EllipticCurve(GF(11^100,'a'),[3,3]).cardinality()
137806123398222701841183371720896367762643312000384671846835266941791510341065565176497846502742959856128
Return the cardinality of self over the base field. Will be called by user function cardinality only when necessary, i.e. when the j_invariant is not in the prime field.
ALGORITHM: A variant of “Mestre’s trick” extended to all finite fields by Cremona and Sutherland, 2008.
Note
- The Mestre-Schoof-Cremona-Sutherland algorithm may fail for a small finite number of curves over
for
at most 49, so for
we use an exhaustive count.
- Quadratic twists are not implemented in characteristic 2 when
; but this case is treated separately.
EXAMPLES:
sage: p=next_prime(10^3)
sage: E=EllipticCurve(GF(p),[3,4])
sage: E.cardinality_bsgs()
1020
sage: E=EllipticCurve(GF(3^4,'a'),[1,1])
sage: E.cardinality_bsgs()
64
sage: F.<a>=GF(101^3,'a')
sage: E=EllipticCurve([2*a^2 + 48*a + 27, 89*a^2 + 76*a + 24])
sage: E.cardinality_bsgs()
1031352
Return the cardinality of self over the base field. Simply adds up the number of points with each x-coordinate: only used for small field sizes!
EXAMPLES:
sage: p=next_prime(10^3)
sage: E=EllipticCurve(GF(p),[3,4])
sage: E.cardinality_exhaustive()
1020
sage: E=EllipticCurve(GF(3^4,'a'),[1,1])
sage: E.cardinality_exhaustive()
64
Return the cardinality of self over the (prime) base field using pari.
The result is not cached.
EXAMPLES:
sage: p=next_prime(10^3)
sage: E=EllipticCurve(GF(p),[3,4])
sage: E.cardinality_pari()
1020
sage: K=GF(next_prime(10^6))
sage: E=EllipticCurve(K,[1,0,0,1,1])
sage: E.cardinality_pari()
999945
TESTS:
sage: K.<a>=GF(3^20)
sage: E=EllipticCurve(K,[1,0,0,1,a])
sage: E.cardinality_pari()
...
ValueError: cardinality_pari() only works over prime fields.
sage: E.cardinality()
3486794310
Return the cardinality of self over the (prime) base field using sea.
INPUT:
The result is not cached.
EXAMPLES:
sage: p=next_prime(10^3)
sage: E=EllipticCurve(GF(p),[3,4])
sage: E.cardinality_sea()
1020
sage: K=GF(next_prime(10^6))
sage: E=EllipticCurve(K,[1,0,0,1,1])
sage: E.cardinality_sea()
999945
TESTS:
sage: K.<a>=GF(3^20)
sage: E=EllipticCurve(K,[1,0,0,1,a])
sage: E.cardinality_sea()
...
ValueError: cardinality_sea() only works over prime fields.
sage: E.cardinality()
3486794310
Returns the cardinality of this elliptic curve over the base field or extensions.
INPUT:
OUTPUT:
If 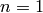 , returns the cardinality of the curve over its base field.
, returns the cardinality of the curve over its base field.
If 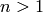 , returns a list
, returns a list ![[c_1, c_2, ..., c_n]](../../../_images/math/bf473d75713c725fffd24e0c869bdcdbc5d5fc97.png) where
where 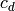 is
the cardinality of the curve over the extension of degree
is
the cardinality of the curve over the extension of degree  of its base field.
of its base field.
EXAMPLES:
sage: p = 101
sage: F = GF(p)
sage: E = EllipticCurve(F, [2,3])
sage: E.count_points(1)
96
sage: E.count_points(5)
[96, 10368, 1031904, 104053248, 10509895776]
sage: F.<a> = GF(p^2)
sage: E = EllipticCurve(F, [a,a])
sage: E.cardinality()
10295
sage: E.count_points()
10295
sage: E.count_points(1)
10295
sage: E.count_points(5)
[10295, 104072155, 1061518108880, 10828567126268595, 110462212555439192375]
Return the frobenius of self as an element of a quadratic order
Note
This computes the curve cardinality, which may be time-consuming.
Frobenius is only determined up to conjugacy.
EXAMPLES:
sage: E=EllipticCurve(GF(11),[3,3])
sage: E.frobenius()
phi
sage: E.frobenius().minpoly()
x^2 - 4*x + 11
For some supersingular curves, Frobenius is in Z:
sage: E=EllipticCurve(GF(25,'a'),[0,0,0,0,1])
sage: E.frobenius()
-5
Return the quadratic order Z[phi] where phi is the Frobenius endomorphism of the elliptic curve
Note
This computes the curve cardinality, which may be time-consuming.
EXAMPLES:
sage: E=EllipticCurve(GF(11),[3,3])
sage: E.frobenius_order()
Order in Number Field in phi with defining polynomial x^2 - 4*x + 11
For some supersingular curves, Frobenius is in Z and the Frobenius order is Z:
sage: E=EllipticCurve(GF(25,'a'),[0,0,0,0,1])
sage: R=E.frobenius_order()
sage: R
Order in Number Field in phi with defining polynomial x + 5
sage: R.degree()
1
Return the characteristic polynomial of Frobenius.
The Frobenius endomorphism of the elliptic curve has quadratic
characteristic polynomial. In most cases this is irreducible and
defines an imaginary quadratic order; for some supersingular
curves, Frobenius is an integer a and the polynomial is
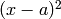 .
.
Note
This computes the curve cardinality, which may be time-consuming.
EXAMPLES:
sage: E=EllipticCurve(GF(11),[3,3])
sage: E.frobenius_polynomial()
x^2 - 4*x + 11
For some supersingular curves, Frobenius is in Z and the polynomial is a square:
sage: E=EllipticCurve(GF(25,'a'),[0,0,0,0,1])
sage: E.frobenius_polynomial().factor()
(x + 5)^2
Returns a tuple of length up to 2 of points which generate the abelian group of points on this elliptic curve. See abelian_group() for limitations.
The algorithm uses random points on the curve, and hence the generators are likely to differ from one run to another; but they are cached so will be consistent in any one run of Sage.
AUTHORS:
EXAMPLES:
sage: E=EllipticCurve(GF(11),[2,5])
sage: E.gens() # random output
((0 : 7 : 1),)
sage: EllipticCurve(GF(41),[2,5]).gens() # random output
((21 : 1 : 1), (8 : 0 : 1))
sage: F.<a>=GF(3^6,'a')
sage: E=EllipticCurve([a,a+1])
sage: pts=E.gens()
sage: len(pts)
1
sage: pts[0].order()==E.cardinality()
True
Returns whether or not self is isogenous to other
INPUT:
OUTPUT:
(bool) True if there is an isogeny from curve self to curve other defined over field.
EXAMPLES:
sage: E1 = EllipticCurve(GF(11^2,'a'),[2,7]); E1
Elliptic Curve defined by y^2 = x^3 + 2*x + 7 over Finite Field in a of size 11^2
sage: E1.is_isogenous(5)
...
ValueError: Second argument is not an Elliptic Curve.
sage: E1.is_isogenous(E1)
True
sage: E2 = EllipticCurve(GF(7^3,'b'),[3,1]); E2
Elliptic Curve defined by y^2 = x^3 + 3*x + 1 over Finite Field in b of size 7^3
sage: E1.is_isogenous(E2)
...
ValueError: The base fields must have the same characteristic.
sage: E3 = EllipticCurve(GF(11^2,'c'),[4,3]); E3
Elliptic Curve defined by y^2 = x^3 + 4*x + 3 over Finite Field in c of size 11^2
sage: E1.is_isogenous(E3)
False
sage: E4 = EllipticCurve(GF(11^6,'d'),[6,5]); E4
Elliptic Curve defined by y^2 = x^3 + 6*x + 5 over Finite Field in d of size 11^6
sage: E1.is_isogenous(E4)
True
sage: E5 = EllipticCurve(GF(11^7,'e'),[4,2]); E5
Elliptic Curve defined by y^2 = x^3 + 4*x + 2 over Finite Field in e of size 11^7
sage: E1.is_isogenous(E5)
...
ValueError: Curves have different base fields: use the field parameter.
When the field is given:
sage: E1 = EllipticCurve(GF(13^2,’a’),[2,7]); E1 Elliptic Curve defined by y^2 = x^3 + 2*x + 7 over Finite Field in a of size 13^2 sage: E1.is_isogenous(5,GF(13^6,’f’)) Traceback (most recent call last): ... ValueError: Second argument is not an Elliptic Curve. sage: E6 = EllipticCurve(GF(11^3,’g’),[9,3]); E6 Elliptic Curve defined by y^2 = x^3 + 9*x + 3 over Finite Field in g of size 11^3 sage: E1.is_isogenous(E6,QQ) Traceback (most recent call last): ... ValueError: The base fields must have the same characteristic. sage: E7 = EllipticCurve(GF(13^5,’h’),[2,9]); E7 Elliptic Curve defined by y^2 = x^3 + 2*x + 9 over Finite Field in h of size 13^5 sage: E1.is_isogenous(E7,GF(13^4,’i’)) Traceback (most recent call last): ... ValueError: Field must be an extension of the base fields of both curves sage: E1.is_isogenous(E7,GF(13^10,’j’)) False sage: E1.is_isogenous(E7,GF(13^30,’j’)) False
Return the number of points on this elliptic curve over an extension field (default: the base field).
INPUT:
algorithm - string (default: ‘heuristic’), used only for point counting over prime fields
- 'heuristic' - use a heuristic to choose between pari, bsgs and sea.
- 'pari' - use the baby step giant step method as implemented in PARI via the C-library function ellap.
- 'sea' - use sea.gp as implemented in PARI by Christophe Doche and Sylvain Duquesne. (‘sea’ stands for ‘Schoof-Elkies-Atkin’.)
- bsgs - use the baby step giant step method as implemented in Sage, with the Cremona - Sutherland version of Mestre’s trick.
- all - (over prime fields only) compute cardinality with all of pari, sea and bsgs; return result if they agree or raise a RuntimeError if they do not.
early_abort - bool (default: False); this is used only by sea. if True, stop early if a small factor of the order is found.
extension_degree - int (default: 1); if the
base field is 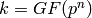 and extension_degree=d, returns
the cardinality of
and extension_degree=d, returns
the cardinality of 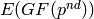 .
.
OUTPUT: an integer
The cardinality is cached.
Over prime fields, one of the above algorithms is used. Over non-prime fields, the serious point counting is done on a standard curve with the same j-invariant over the field GF(p)(j), then lifted to the base_field, and finally account is taken of twists.
For j=0 and j=1728 special formulas are used instead.
EXAMPLES:
sage: EllipticCurve(GF(4,'a'),[1,2,3,4,5]).cardinality()
8
sage: k.<a> = GF(3^3)
sage: l = [a^2 + 1, 2*a^2 + 2*a + 1, a^2 + a + 1, 2, 2*a]
sage: EllipticCurve(k,l).cardinality()
29
sage: l = [1, 1, 0, 2, 0]
sage: EllipticCurve(k,l).cardinality()
38
An even bigger extension (which we check against Magma):
sage: EllipticCurve(GF(3^100,'a'),[1,2,3,4,5]).cardinality()
515377520732011331036459693969645888996929981504
sage: magma.eval("Order(EllipticCurve([GF(3^100)|1,2,3,4,5]))") # optional - magma
'515377520732011331036459693969645888996929981504'
sage: EllipticCurve(GF(10007),[1,2,3,4,5]).cardinality()
10076
sage: EllipticCurve(GF(10007),[1,2,3,4,5]).cardinality(algorithm='sea')
10076
sage: EllipticCurve(GF(10007),[1,2,3,4,5]).cardinality(algorithm='pari')
10076
sage: EllipticCurve(GF(next_prime(10**20)),[1,2,3,4,5]).cardinality(algorithm='sea')
100000000011093199520
The cardinality is cached:
sage: E = EllipticCurve(GF(3^100,'a'),[1,2,3,4,5])
sage: E.cardinality() is E.cardinality()
True
sage: E=EllipticCurve(GF(11^2,'a'),[3,3])
sage: E.cardinality()
128
sage: EllipticCurve(GF(11^100,'a'),[3,3]).cardinality()
137806123398222701841183371720896367762643312000384671846835266941791510341065565176497846502742959856128
Draw a graph of this elliptic curve over a prime finite field.
INPUT:
EXAMPLES:
sage: E = EllipticCurve(FiniteField(17), [0,1])
sage: P = plot(E, rgbcolor=(0,0,1))
All the points on this elliptic curve. The list of points is cached so subsequent calls are free.
EXAMPLES:
sage: p = 5
sage: F = GF(p)
sage: E = EllipticCurve(F, [1, 3])
sage: a_sub_p = E.change_ring(QQ).ap(p); a_sub_p
2
sage: len(E.points())
4
sage: p + 1 - a_sub_p
4
sage: E.points()
[(0 : 1 : 0), (1 : 0 : 1), (4 : 1 : 1), (4 : 4 : 1)]
sage: K = GF(p**2,'a')
sage: E = E.change_ring(K)
sage: len(E.points())
32
sage: (p + 1)**2 - a_sub_p**2
32
sage: w = E.points(); w
[(0 : 1 : 0), (0 : 2*a + 4 : 1), (0 : 3*a + 1 : 1), (1 : 0 : 1), (2 : 2*a + 4 : 1), (2 : 3*a + 1 : 1), (3 : 2*a + 4 : 1), (3 : 3*a + 1 : 1), (4 : 1 : 1), (4 : 4 : 1), (a : 1 : 1), (a : 4 : 1), (a + 2 : a + 1 : 1), (a + 2 : 4*a + 4 : 1), (a + 3 : a : 1), (a + 3 : 4*a : 1), (a + 4 : 0 : 1), (2*a : 2*a : 1), (2*a : 3*a : 1), (2*a + 4 : a + 1 : 1), (2*a + 4 : 4*a + 4 : 1), (3*a + 1 : a + 3 : 1), (3*a + 1 : 4*a + 2 : 1), (3*a + 2 : 2*a + 3 : 1), (3*a + 2 : 3*a + 2 : 1), (4*a : 0 : 1), (4*a + 1 : 1 : 1), (4*a + 1 : 4 : 1), (4*a + 3 : a + 3 : 1), (4*a + 3 : 4*a + 2 : 1), (4*a + 4 : a + 4 : 1), (4*a + 4 : 4*a + 1 : 1)]
Note that the returned list is an immutable sorted Sequence:
sage: w[0] = 9
...
ValueError: object is immutable; please change a copy instead.
Returns a random point on this elliptic curve.
If  is small, finds all points and returns one at random.
Otherwise, returns the point at infinity with probability
is small, finds all points and returns one at random.
Otherwise, returns the point at infinity with probability
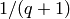 where the base field has cardinality
where the base field has cardinality  , and then
picks random
, and then
picks random  -coordinates from the base field until one
gives a rational point.
-coordinates from the base field until one
gives a rational point.
EXAMPLES:
sage: k = GF(next_prime(7^5))
sage: E = EllipticCurve(k,[2,4])
sage: P = E.random_element(); P
(16740 : 12486 : 1)
sage: type(P)
<class 'sage.schemes.elliptic_curves.ell_point.EllipticCurvePoint_finite_field'>
sage: P in E
True
sage: k.<a> = GF(7^5)
sage: E = EllipticCurve(k,[2,4])
sage: P = E.random_element(); P
(2*a^4 + 3*a^3 + 5*a^2 + 6*a + 4 : 6*a^4 + 4*a^3 + a + 6 : 1)
sage: type(P)
<class 'sage.schemes.elliptic_curves.ell_point.EllipticCurvePoint_finite_field'>
sage: P in E
True
sage: k.<a> = GF(2^5)
sage: E = EllipticCurve(k,[a^2,a,1,a+1,1])
sage: P = E.random_element(); P
(a^4 + a^2 + 1 : a^3 + a : 1)
sage: type(P)
<class 'sage.schemes.elliptic_curves.ell_point.EllipticCurvePoint_finite_field'>
sage: P in E
True
Ensure that the entire point set is reachable:
sage: E = EllipticCurve(GF(11), [2,1])
sage: len(set(E.random_element() for _ in range(100)))
16
sage: E.cardinality()
16
TESTS:
See trac #8311:
sage: E = EllipticCurve(GF(3), [0,0,0,2,2])
sage: E.random_element()
(0 : 1 : 0)
sage: E.cardinality()
1
sage: E = EllipticCurve(GF(2), [0,0,1,1,1])
sage: E.random_point()
(0 : 1 : 0)
sage: E.cardinality()
1
sage: F.<a> = GF(4)
sage: E = EllipticCurve(F, [0, 0, 1, 0, a])
sage: E.random_point()
(0 : 1 : 0)
sage: E.cardinality()
1
Returns a random point on this elliptic curve.
If  is small, finds all points and returns one at random.
Otherwise, returns the point at infinity with probability
is small, finds all points and returns one at random.
Otherwise, returns the point at infinity with probability
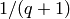 where the base field has cardinality
where the base field has cardinality  , and then
picks random
, and then
picks random  -coordinates from the base field until one
gives a rational point.
-coordinates from the base field until one
gives a rational point.
EXAMPLES:
sage: k = GF(next_prime(7^5))
sage: E = EllipticCurve(k,[2,4])
sage: P = E.random_element(); P
(16740 : 12486 : 1)
sage: type(P)
<class 'sage.schemes.elliptic_curves.ell_point.EllipticCurvePoint_finite_field'>
sage: P in E
True
sage: k.<a> = GF(7^5)
sage: E = EllipticCurve(k,[2,4])
sage: P = E.random_element(); P
(2*a^4 + 3*a^3 + 5*a^2 + 6*a + 4 : 6*a^4 + 4*a^3 + a + 6 : 1)
sage: type(P)
<class 'sage.schemes.elliptic_curves.ell_point.EllipticCurvePoint_finite_field'>
sage: P in E
True
sage: k.<a> = GF(2^5)
sage: E = EllipticCurve(k,[a^2,a,1,a+1,1])
sage: P = E.random_element(); P
(a^4 + a^2 + 1 : a^3 + a : 1)
sage: type(P)
<class 'sage.schemes.elliptic_curves.ell_point.EllipticCurvePoint_finite_field'>
sage: P in E
True
Ensure that the entire point set is reachable:
sage: E = EllipticCurve(GF(11), [2,1])
sage: len(set(E.random_element() for _ in range(100)))
16
sage: E.cardinality()
16
TESTS:
See trac #8311:
sage: E = EllipticCurve(GF(3), [0,0,0,2,2])
sage: E.random_element()
(0 : 1 : 0)
sage: E.cardinality()
1
sage: E = EllipticCurve(GF(2), [0,0,1,1,1])
sage: E.random_point()
(0 : 1 : 0)
sage: E.cardinality()
1
sage: F.<a> = GF(4)
sage: E = EllipticCurve(F, [0, 0, 1, 0, a])
sage: E.random_point()
(0 : 1 : 0)
sage: E.cardinality()
1
All the points on this elliptic curve. The list of points is cached so subsequent calls are free.
EXAMPLES:
sage: p = 5
sage: F = GF(p)
sage: E = EllipticCurve(F, [1, 3])
sage: a_sub_p = E.change_ring(QQ).ap(p); a_sub_p
2
sage: len(E.points())
4
sage: p + 1 - a_sub_p
4
sage: E.points()
[(0 : 1 : 0), (1 : 0 : 1), (4 : 1 : 1), (4 : 4 : 1)]
sage: K = GF(p**2,'a')
sage: E = E.change_ring(K)
sage: len(E.points())
32
sage: (p + 1)**2 - a_sub_p**2
32
sage: w = E.points(); w
[(0 : 1 : 0), (0 : 2*a + 4 : 1), (0 : 3*a + 1 : 1), (1 : 0 : 1), (2 : 2*a + 4 : 1), (2 : 3*a + 1 : 1), (3 : 2*a + 4 : 1), (3 : 3*a + 1 : 1), (4 : 1 : 1), (4 : 4 : 1), (a : 1 : 1), (a : 4 : 1), (a + 2 : a + 1 : 1), (a + 2 : 4*a + 4 : 1), (a + 3 : a : 1), (a + 3 : 4*a : 1), (a + 4 : 0 : 1), (2*a : 2*a : 1), (2*a : 3*a : 1), (2*a + 4 : a + 1 : 1), (2*a + 4 : 4*a + 4 : 1), (3*a + 1 : a + 3 : 1), (3*a + 1 : 4*a + 2 : 1), (3*a + 2 : 2*a + 3 : 1), (3*a + 2 : 3*a + 2 : 1), (4*a : 0 : 1), (4*a + 1 : 1 : 1), (4*a + 1 : 4 : 1), (4*a + 3 : a + 3 : 1), (4*a + 3 : 4*a + 2 : 1), (4*a + 4 : a + 4 : 1), (4*a + 4 : 4*a + 1 : 1)]
Note that the returned list is an immutable sorted Sequence:
sage: w[0] = 9
...
ValueError: object is immutable; please change a copy instead.
Return the trace of Frobenius acting on this elliptic curve.
Note
This computes the curve cardinality, which may be time-consuming.
EXAMPLES:
sage: E=EllipticCurve(GF(101),[2,3])
sage: E.trace_of_frobenius()
6
sage: E=EllipticCurve(GF(11^5,'a'),[2,5])
sage: E.trace_of_frobenius()
802
The following shows that the issue from trac #2849 is fixed:
sage: E=EllipticCurve(GF(3^5,'a'),[-1,-1])
sage: E.trace_of_frobenius()
-27