An elliptic curve  over a number field
over a number field  can be given
by a Weierstrass equation whose coefficients lie in
can be given
by a Weierstrass equation whose coefficients lie in  or by
using base_extend on an elliptic curve defined over a subfield.
or by
using base_extend on an elliptic curve defined over a subfield.
One major difference to elliptic curves over  is that there
might not exist a global minimal equation over
is that there
might not exist a global minimal equation over  , when
, when  does
not have class number one.
Another difference is the lack of understanding of modularity for
general elliptic curves over general number fields.
does
not have class number one.
Another difference is the lack of understanding of modularity for
general elliptic curves over general number fields.
Currently sage can obtain local information about 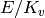 for finite
place
for finite
place  , it has an interface to Denis Simon’s script for 2-descent,
it can compute the torsion subgroup of the Mordell-Weil group
, it has an interface to Denis Simon’s script for 2-descent,
it can compute the torsion subgroup of the Mordell-Weil group 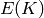 ,
and it can work with isogenies defined over
,
and it can work with isogenies defined over  .
.
EXAMPLE:
sage: K.<i> = NumberField(x^2+1)
sage: E = EllipticCurve([0,4+i])
sage: E.discriminant()
-3456*i - 6480
sage: P= E([i,2])
sage: P+P
(-2*i + 9/16 : -9/4*i - 101/64 : 1)
sage: E.has_good_reduction(2+i)
True
sage: E.local_data(4+i)
Local data at Fractional ideal (i + 4):
Reduction type: bad additive
Local minimal model: Elliptic Curve defined by y^2 = x^3 + (i+4) over Number Field in i with defining polynomial x^2 + 1
Minimal discriminant valuation: 2
Conductor exponent: 2
Kodaira Symbol: II
Tamagawa Number: 1
sage: E.tamagawa_product_bsd()
1
sage: E.simon_two_descent()
(1, 1, [(i : 2 : 1)])
sage: E.torsion_order()
1
sage: E.isogenies_prime_degree(3)
[Isogeny of degree 3 from Elliptic Curve defined by y^2 = x^3 + (i+4) over Number Field in i with defining polynomial x^2 + 1 to Elliptic Curve defined by y^2 = x^3 + (-27*i-108) over Number Field in i with defining polynomial x^2 + 1]
AUTHORS:
REFERENCE:
Bases: sage.schemes.elliptic_curves.ell_field.EllipticCurve_field
Elliptic curve over a number field.
EXAMPLES:
sage: K.<i>=NumberField(x^2+1)
sage: EllipticCurve([i, i - 1, i + 1, 24*i + 15, 14*i + 35])
Elliptic Curve defined by y^2 + i*x*y + (i+1)*y = x^3 + (i-1)*x^2 + (24*i+15)*x + (14*i+35) over Number Field in i with defining polynomial x^2 + 1
Returns the conductor of this elliptic curve as a fractional ideal of the base field.
OUTPUT:
(fractional ideal) The conductor of the curve.
EXAMPLES:
sage: K.<i>=NumberField(x^2+1)
sage: EllipticCurve([i, i - 1, i + 1, 24*i + 15, 14*i + 35]).conductor()
Fractional ideal (21*i - 3)
sage: K.<a>=NumberField(x^2-x+3)
sage: EllipticCurve([1 + a , -1 + a , 1 + a , -11 + a , 5 -9*a ]).conductor()
Fractional ideal (-6*a)
A not so well known curve with everywhere good reduction:
sage: K.<a>=NumberField(x^2-38)
sage: E=EllipticCurve([0,0,0, 21796814856932765568243810*a - 134364590724198567128296995, 121774567239345229314269094644186997594*a - 750668847495706904791115375024037711300])
sage: E.conductor()
Fractional ideal (1)
An example which used to fail (see trac #5307):
sage: K.<w>=NumberField(x^2+x+6)
sage: E=EllipticCurve([w,-1,0,-w-6,0])
sage: E.conductor()
Fractional ideal (86304, w + 5898)
Return a model of self which is integral at all primes.
EXAMPLES:
sage: K.<i> = NumberField(x^2+1)
sage: E = EllipticCurve([i/5,i/5,i/5,i/5,i/5])
sage: P1,P2 = K.primes_above(5)
sage: E.global_integral_model()
Elliptic Curve defined by y^2 + (-i)*x*y + (-25*i)*y = x^3 + 5*i*x^2 + 125*i*x + 3125*i over Number Field in i with defining polynomial x^2 + 1
trac # 7935:
sage: K.<a> = NumberField(x^2-38)
sage: E = EllipticCurve([a,1/2])
sage: E.global_integral_model()
Elliptic Curve defined by y^2 = x^3 + 1444*a*x + 27436 over Number Field in a with defining polynomial x^2 - 38
Returns a model of self that is integral, minimal at all primes.
Note
This is only implemented for class number 1. In general, such a model may or may not exist.
INPUT:
OUTPUT:
A global integral and minimal model.
EXAMPLES:
sage: K.<a> = NumberField(x^2-38)
sage: E = EllipticCurve([0,0,0, 21796814856932765568243810*a - 134364590724198567128296995, 121774567239345229314269094644186997594*a - 750668847495706904791115375024037711300])
sage: E2 = E.global_minimal_model()
sage: E2 # random (the global minimal model is not unique)
Elliptic Curve defined by y^2 + a*x*y + (a+1)*y = x^3 + (a+1)*x^2 + (368258520200522046806318444*a-2270097978636731786720859345)*x + (8456608930173478039472018047583706316424*a-52130038506793883217874390501829588391299) over Number Field in a with defining polynomial x^2 - 38
sage: E2.local_data()
[]
Return True if this elliptic curve has (bad) additive reduction at the prime  .
.
INPUT:
OUTPUT:
(bool) True if the curve has additive reduction at  , else False.
, else False.
EXAMPLES:
sage: E=EllipticCurve('27a1')
sage: [(p,E.has_additive_reduction(p)) for p in prime_range(15)]
[(2, False), (3, True), (5, False), (7, False), (11, False), (13, False)]
sage: K.<a>=NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.has_additive_reduction(p)) for p in [P17a,P17b]]
[(Fractional ideal (4*a^2 - 2*a + 1), False),
(Fractional ideal (2*a + 1), True)]
Return True if this elliptic curve has bad reduction at the prime  .
.
INPUT:
OUTPUT:
(bool) True if the curve has bad reduction at  , else False.
, else False.
Note
This requires determining a local integral minimal model; we do not just check that the discriminant of the current model has valuation zero.
EXAMPLES:
sage: E=EllipticCurve('14a1')
sage: [(p,E.has_bad_reduction(p)) for p in prime_range(15)]
[(2, True), (3, False), (5, False), (7, True), (11, False), (13, False)]
sage: K.<a>=NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.has_bad_reduction(p)) for p in [P17a,P17b]]
[(Fractional ideal (4*a^2 - 2*a + 1), False),
(Fractional ideal (2*a + 1), True)]
Return True if this elliptic curve has good reduction at the prime  .
.
INPUT:
OUTPUT:
(bool) – True if the curve has good reduction at  , else False.
, else False.
Note
This requires determining a local integral minimal model; we do not just check that the discriminant of the current model has valuation zero.
EXAMPLES:
sage: E=EllipticCurve('14a1')
sage: [(p,E.has_good_reduction(p)) for p in prime_range(15)]
[(2, False), (3, True), (5, True), (7, False), (11, True), (13, True)]
sage: K.<a>=NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.has_good_reduction(p)) for p in [P17a,P17b]]
[(Fractional ideal (4*a^2 - 2*a + 1), True),
(Fractional ideal (2*a + 1), False)]
Return True if this elliptic curve has (bad) multiplicative reduction at the prime  .
.
Note
See also has_split_multiplicative_reduction() and has_nonsplit_multiplicative_reduction().
INPUT:
element generating such an ideal.
OUTPUT:
(bool) True if the curve has multiplicative reduction at  ,
else False.
,
else False.
EXAMPLES:
sage: E=EllipticCurve('14a1')
sage: [(p,E.has_multiplicative_reduction(p)) for p in prime_range(15)]
[(2, True), (3, False), (5, False), (7, True), (11, False), (13, False)]
sage: K.<a>=NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.has_multiplicative_reduction(p)) for p in [P17a,P17b]]
[(Fractional ideal (4*a^2 - 2*a + 1), False), (Fractional ideal (2*a + 1), False)]
Return True if this elliptic curve has (bad) non-split multiplicative reduction at the prime  .
.
INPUT:
OUTPUT:
(bool) True if the curve has non-split multiplicative
reduction at  , else False.
, else False.
EXAMPLES:
sage: E=EllipticCurve('14a1')
sage: [(p,E.has_nonsplit_multiplicative_reduction(p)) for p in prime_range(15)]
[(2, True), (3, False), (5, False), (7, False), (11, False), (13, False)]
sage: K.<a>=NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.has_nonsplit_multiplicative_reduction(p)) for p in [P17a,P17b]]
[(Fractional ideal (4*a^2 - 2*a + 1), False), (Fractional ideal (2*a + 1), False)]
Return True if this elliptic curve has (bad) split multiplicative reduction at the prime  .
.
INPUT:
OUTPUT:
(bool) True if the curve has split multiplicative reduction at
 , else False.
, else False.
EXAMPLES:
sage: E=EllipticCurve('14a1')
sage: [(p,E.has_split_multiplicative_reduction(p)) for p in prime_range(15)]
[(2, False), (3, False), (5, False), (7, True), (11, False), (13, False)]
sage: K.<a>=NumberField(x^3-2)
sage: P17a, P17b = [P for P,e in K.factor(17)]
sage: E = EllipticCurve([0,0,0,0,2*a+1])
sage: [(p,E.has_split_multiplicative_reduction(p)) for p in [P17a,P17b]]
[(Fractional ideal (4*a^2 - 2*a + 1), False), (Fractional ideal (2*a + 1), False)]
Return a model of self which is integral at all primes.
EXAMPLES:
sage: K.<i> = NumberField(x^2+1)
sage: E = EllipticCurve([i/5,i/5,i/5,i/5,i/5])
sage: P1,P2 = K.primes_above(5)
sage: E.global_integral_model()
Elliptic Curve defined by y^2 + (-i)*x*y + (-25*i)*y = x^3 + 5*i*x^2 + 125*i*x + 3125*i over Number Field in i with defining polynomial x^2 + 1
trac # 7935:
sage: K.<a> = NumberField(x^2-38)
sage: E = EllipticCurve([a,1/2])
sage: E.global_integral_model()
Elliptic Curve defined by y^2 = x^3 + 1444*a*x + 27436 over Number Field in a with defining polynomial x^2 - 38
Return true iff self is integral at all primes.
EXAMPLES:
sage: K.<i> = NumberField(x^2+1)
sage: E = EllipticCurve([i/5,i/5,i/5,i/5,i/5])
sage: P1,P2 = K.primes_above(5)
sage: Emin = E.global_integral_model()
sage: Emin.is_global_integral_model()
True
Returns whether or not self is isogenous to other.
INPUT:
 for all primes
for all primes  of
norm up to maxp. If True, the function returns
False when the previous condition does not hold, and if it
does hold we attempt to see if the curves are indeed
isogenous. However, this has not been fully implemented
(see examples below), so we may not be able to determine
whether or not the curves are isogenous..
of
norm up to maxp. If True, the function returns
False when the previous condition does not hold, and if it
does hold we attempt to see if the curves are indeed
isogenous. However, this has not been fully implemented
(see examples below), so we may not be able to determine
whether or not the curves are isogenous.. for which isogeny modulo
for which isogeny modulo  will be checked.
will be checked.OUTPUT:
(bool) True if there is an isogeny from curve self to curve other.
EXAMPLES:
sage: x = polygen(QQ, 'x')
sage: F = NumberField(x^2 -2, 's'); F
Number Field in s with defining polynomial x^2 - 2
sage: E1 = EllipticCurve(F, [7,8])
sage: E2 = EllipticCurve(F, [0,5,0,1,0])
sage: E3 = EllipticCurve(F, [0,-10,0,21,0])
sage: E1.is_isogenous(E2)
False
sage: E1.is_isogenous(E1)
True
sage: E2.is_isogenous(E2)
True
sage: E2.is_isogenous(E1)
False
sage: E2.is_isogenous(E3)
True
sage: x = polygen(QQ, 'x')
sage: F = NumberField(x^2 -2, 's'); F
Number Field in s with defining polynomial x^2 - 2
sage: E = EllipticCurve('14a1')
sage: EE = EllipticCurve('14a2')
sage: E1 = E.change_ring(F)
sage: E2 = EE.change_ring(F)
sage: E1.is_isogenous(E2)
True
sage: x = polygen(QQ, 'x')
sage: F = NumberField(x^2 -2, 's'); F
Number Field in s with defining polynomial x^2 - 2
sage: k.<a> = NumberField(x^3+7)
sage: E = EllipticCurve(F, [7,8])
sage: EE = EllipticCurve(k, [2, 2])
sage: E.is_isogenous(EE)
...
ValueError: Second argument must be defined over the same number field.
Some examples from Cremona’s 1981 tables:
sage: K.<i> = QuadraticField(-1)
sage: E1 = EllipticCurve([i + 1, 0, 1, -240*i - 400, -2869*i - 2627])
sage: E1.conductor()
Fractional ideal (-7*i + 4)
sage: E2 = EllipticCurve([1+i,0,1,0,0])
sage: E2.conductor()
Fractional ideal (-7*i + 4)
sage: E1.is_isogenous(E2)
...
NotImplementedError: Curves appear to be isogenous (same conductor, isogenous modulo all primes of norm up to 1000), but no isogeny has been constructed.
sage: E1.is_isogenous(E2, proof=False)
True
In this case E1 and E2 are in fact 9-isogenous, as may be deduced from the following:
sage: E3 = EllipticCurve([i + 1, 0, 1, -5*i - 5, -2*i - 5])
sage: E3.is_isogenous(E1)
True
sage: E3.is_isogenous(E2)
True
sage: E1.isogeny_degree(E2)
9
Tests if self is integral at the prime ideal  , or at all the
primes if
, or at all the
primes if  is a list or tuple.
is a list or tuple.
INPUT:
EXAMPLES:
sage: K.<i> = NumberField(x^2+1)
sage: P1,P2 = K.primes_above(5)
sage: E = EllipticCurve([i/5,i/5,i/5,i/5,i/5])
sage: E.is_local_integral_model(P1,P2)
False
sage: Emin = E.local_integral_model(P1,P2)
sage: Emin.is_local_integral_model(P1,P2)
True
Returns the minimal degree of an isogeny between self and other, or 0 if no isogeny exists.
INPUT:
OUTPUT:
(int) The degree of an isogeny from self to other, or 0.
Warning
Not all isogenies over number fields are yet implemented. Currently the code only works if there is a chain of isogenies from self to other of degrees 2, 3, 5, 7 and 13.
EXAMPLES:
sage: x = QQ['x'].0
sage: F = NumberField(x^2 -2, 's'); F
Number Field in s with defining polynomial x^2 - 2
sage: E = EllipticCurve('14a1')
sage: EE = EllipticCurve('14a2')
sage: E1 = E.change_ring(F)
sage: E2 = EE.change_ring(F)
sage: E1.isogeny_degree(E2)
2
sage: E2.isogeny_degree(E2)
1
sage: E5 = EllipticCurve('14a5').change_ring(F)
sage: E1.isogeny_degree(E5)
6
Returns the Kodaira Symbol of this elliptic curve at the prime  .
.
INPUT:
OUTPUT:
The Kodaira Symbol of the curve at P, represented as a string.
EXAMPLES:
sage: K.<a>=NumberField(x^2-5)
sage: E=EllipticCurve([20, 225, 750, 625*a + 6875, 31250*a + 46875])
sage: bad_primes = E.discriminant().support(); bad_primes
[Fractional ideal (-a),
Fractional ideal (7/2*a - 81/2),
Fractional ideal (a + 52),
Fractional ideal (2)]
sage: [E.kodaira_symbol(P) for P in bad_primes]
[I0, I1, I1, II]
sage: K.<a> = QuadraticField(-11)
sage: E = EllipticCurve('11a1').change_ring(K)
sage: [E.kodaira_symbol(P) for P in K(11).support()]
[I10]
Local data for this elliptic curve at the prime  .
.
INPUT:
OUTPUT:
If  is specified, returns the EllipticCurveLocalData
object associated to the prime
is specified, returns the EllipticCurveLocalData
object associated to the prime  for this curve. Otherwise,
returns a list of such objects, one for each prime
for this curve. Otherwise,
returns a list of such objects, one for each prime  in the
support of the discriminant of this model.
in the
support of the discriminant of this model.
Note
The model is not required to be integral on input.
For principal  , a generator is used as a uniformizer,
and integrality or minimality at other primes is not
affected. For non-principal
, a generator is used as a uniformizer,
and integrality or minimality at other primes is not
affected. For non-principal  , the minimal model
returned will preserve integrality at other primes, but not
minimality.
, the minimal model
returned will preserve integrality at other primes, but not
minimality.
EXAMPLES:
sage: K.<i> = NumberField(x^2+1)
sage: E = EllipticCurve([1 + i, 0, 1, 0, 0])
sage: E.local_data()
[Local data at Fractional ideal (2*i + 1):
Reduction type: bad non-split multiplicative
Local minimal model: Elliptic Curve defined by y^2 + (i+1)*x*y + y = x^3 over Number Field in i with defining polynomial x^2 + 1
Minimal discriminant valuation: 1
Conductor exponent: 1
Kodaira Symbol: I1
Tamagawa Number: 1,
Local data at Fractional ideal (-3*i - 2):
Reduction type: bad split multiplicative
Local minimal model: Elliptic Curve defined by y^2 + (i+1)*x*y + y = x^3 over Number Field in i with defining polynomial x^2 + 1
Minimal discriminant valuation: 2
Conductor exponent: 1
Kodaira Symbol: I2
Tamagawa Number: 2]
sage: E.local_data(K.ideal(3))
Local data at Fractional ideal (3):
Reduction type: good
Local minimal model: Elliptic Curve defined by y^2 + (i+1)*x*y + y = x^3 over Number Field in i with defining polynomial x^2 + 1
Minimal discriminant valuation: 0
Conductor exponent: 0
Kodaira Symbol: I0
Tamagawa Number: 1
An example raised in #3897:
sage: E = EllipticCurve([1,1])
sage: E.local_data(3)
Local data at Principal ideal (3) of Integer Ring:
Reduction type: good
Local minimal model: Elliptic Curve defined by y^2 = x^3 + x + 1 over Rational Field
Minimal discriminant valuation: 0
Conductor exponent: 0
Kodaira Symbol: I0
Tamagawa Number: 1
Return a model of self which is integral at the prime ideal
 .
.
Note
The integrality at other primes is not affected, even if
 is non-principal.
is non-principal.
INPUT:
EXAMPLES:
sage: K.<i> = NumberField(x^2+1)
sage: P1,P2 = K.primes_above(5)
sage: E = EllipticCurve([i/5,i/5,i/5,i/5,i/5])
sage: E.local_integral_model((P1,P2))
Elliptic Curve defined by y^2 + (-i)*x*y + (-25*i)*y = x^3 + 5*i*x^2 + 125*i*x + 3125*i over Number Field in i with defining polynomial x^2 + 1
Returns a model which is integral at all primes and minimal at  .
.
INPUT:
OUTPUT:
A model of the curve which is minimal (and integral) at  .
.
Note
The model is not required to be integral on input.
For principal  , a generator is used as a uniformizer,
and integrality or minimality at other primes is not
affected. For non-principal
, a generator is used as a uniformizer,
and integrality or minimality at other primes is not
affected. For non-principal  , the minimal model
returned will preserve integrality at other primes, but not
minimality.
, the minimal model
returned will preserve integrality at other primes, but not
minimality.
EXAMPLES:
sage: K.<a>=NumberField(x^2-5)
sage: E=EllipticCurve([20, 225, 750, 625*a + 6875, 31250*a + 46875])
sage: P=K.ideal(a)
sage: E.local_minimal_model(P).ainvs()
(0, 1, 0, a - 33, -2*a + 64)
Returns the period lattice of the elliptic curve for the given embedding of its base field.
INPUT:
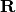 or
or 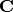 .
.Note
The precision of the embedding is ignored: we only use the given embedding to determine which embedding into QQbar to use. Once the lattice has been initialized, periods can be computed to arbitrary precision.
EXAMPLES:
First define a field with two real embeddings:
sage: K.<a> = NumberField(x^3-2)
sage: E=EllipticCurve([0,0,0,a,2])
sage: embs=K.embeddings(CC); len(embs)
3
For each embedding we have a different period lattice:
sage: E.period_lattice(embs[0])
Period lattice associated to Elliptic Curve defined by y^2 = x^3 + a*x + 2 over Number Field in a with defining polynomial x^3 - 2 with respect to the embedding Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Algebraic Field
Defn: a |--> -0.6299605249474365? - 1.091123635971722?*I
sage: E.period_lattice(embs[1])
Period lattice associated to Elliptic Curve defined by y^2 = x^3 + a*x + 2 over Number Field in a with defining polynomial x^3 - 2 with respect to the embedding Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Algebraic Field
Defn: a |--> -0.6299605249474365? + 1.091123635971722?*I
sage: E.period_lattice(embs[2])
Period lattice associated to Elliptic Curve defined by y^2 = x^3 + a*x + 2 over Number Field in a with defining polynomial x^3 - 2 with respect to the embedding Ring morphism:
From: Number Field in a with defining polynomial x^3 - 2
To: Algebraic Field
Defn: a |--> 1.259921049894873?
Although the original embeddings have only the default precision, we can obtain the basis with higher precision later:
sage: L=E.period_lattice(embs[0])
sage: L.basis()
(1.86405007647981 - 0.903761485143226*I, -0.149344633143919 - 2.06619546272945*I)
sage: L.basis(prec=100)
(1.8640500764798108425920506200 - 0.90376148514322594749786960975*I, -0.14934463314391922099120107422 - 2.0661954627294548995621225062*I)
Return the reduction of the elliptic curve at a place of good reduction.
INPUT:
OUTPUT:
An elliptic curve over a finite field, the residue field of the place.
EXAMPLES:
sage: K.<i> = QuadraticField(-1)
sage: EK = EllipticCurve([0,0,0,i,i+3])
sage: v = K.fractional_ideal(2*i+3)
sage: EK.reduction(v)
Elliptic Curve defined by y^2 = x^3 + 5*x + 8 over Residue field of Fractional ideal (2*i + 3)
sage: EK.reduction(K.ideal(1+i))
...
ValueError: The curve must have good reduction at the place.
sage: EK.reduction(K.ideal(2))
...
ValueError: The ideal must be prime.
Computes lower and upper bounds on the rank of the Mordell-Weil group, and a list of independent points.
INPUT:
OUTPUT:
(lower, upper, list) where lower is a lower bound on the rank, upper is an upper bound (the 2-Selmer rank) and list is a list of independent points on the Weierstrass model. The length of list is equal to either lower, or lower-1, since when lower is less than upper and of different parity, the value of lower is increased by 1.
Note
For non-quadratic number fields, this code does return, but it takes a long time.
IMPLEMENTATION:
Uses Denis Simon’s GP/PARI scripts from url{http://www.math.unicaen.fr/~simon/}.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 23, 'a')
sage: E = EllipticCurve(K, '37')
sage: E == loads(dumps(E))
True
sage: E.simon_two_descent()
(2, 2, [(-1 : 0 : 1), (1/2*a - 5/2 : -1/2*a - 13/2 : 1)])
sage: K.<a> = NumberField(x^2 + 7, 'a')
sage: E = EllipticCurve(K, [0,0,0,1,a]); E
Elliptic Curve defined by y^2 = x^3 + x + a over Number Field in a with defining polynomial x^2 + 7
sage: v = E.simon_two_descent(verbose=1); v
courbe elliptique : Y^2 = x^3 + Mod(1, y^2 + 7)*x + Mod(y, y^2 + 7)
points triviaux sur la courbe = [[1, 1, 0], [Mod(1/2*y + 3/2, y^2 + 7), Mod(-y - 2, y^2 + 7), 1]]
#S(E/K)[2] = 2
#E(K)/2E(K) = 2
#III(E/K)[2] = 1
rang(E/K) = 1
listpointsmwr = [[Mod(1/2*y + 3/2, y^2 + 7), Mod(-y - 2, y^2 + 7), 1]]
(1, 1, [(1/2*a + 3/2 : -a - 2 : 1)])
sage: v = E.simon_two_descent(verbose=2); v
K = bnfinit(y^2 + 7);
a = Mod(y,K.pol);
bnfellrank(K, [0,0,0,1,a]);
courbe elliptique : Y^2 = x^3 + Mod(1, y^2 + 7)*x + Mod(y, y^2 + 7)
A = 0
B = Mod(1, y^2 + 7)
C = Mod(y, y^2 + 7)
LS2gen = [Mod(Mod(-5, y^2 + 7)*x^2 + Mod(-3*y, y^2 + 7)*x + Mod(8, y^2 + 7), x^3 + Mod(1, y^2 + 7)*x + Mod(y, y^2 + 7)), Mod(Mod(1, y^2 + 7)*x^2 + Mod(1/2*y - 1/2, y^2 + 7)*x - 1, x^3 + Mod(1, y^2 + 7)*x + Mod(y, y^2 + 7))]
#LS2gen = 2
Recherche de points triviaux sur la courbe
points triviaux sur la courbe = [[1, 1, 0], [Mod(1/2*y + 3/2, y^2 + 7), Mod(-y - 2, y^2 + 7), 1]]
zc = Mod(Mod(-5, y^2 + 7)*x^2 + Mod(-3*y, y^2 + 7)*x + Mod(8, y^2 + 7), x^3 + Mod(1, y^2 + 7)*x + Mod(y, y^2 + 7))
symbole de Hilbert (Mod(2, y^2 + 7),Mod(-5, y^2 + 7)) = -1
zc = Mod(Mod(1, y^2 + 7)*x^2 + Mod(1/2*y - 1/2, y^2 + 7)*x + Mod(-1, y^2 + 7), x^3 + Mod(1, y^2 + 7)*x + Mod(y, y^2 + 7))
symbole de Hilbert (Mod(-2*y + 2, y^2 + 7),Mod(1, y^2 + 7)) = 0
sol de Legendre = [1, 0, 1]~
zc*z1^2 = Mod(Mod(2*y - 2, y^2 + 7)*x + Mod(2*y + 10, y^2 + 7), x^3 + Mod(1, y^2 + 7)*x + Mod(y, y^2 + 7))
quartique : (-1/2*y + 1/2)*Y^2 = x^4 + (-3*y - 15)*x^2 + (-8*y - 16)*x + (-11/2*y - 15/2)
reduite: Y^2 = (-1/2*y + 1/2)*x^4 - 4*x^3 + (-3*y + 3)*x^2 + (2*y - 2)*x + (1/2*y + 3/2)
non ELS en [2, [0, 1]~, 1, 1, [1, 1]~]
zc = Mod(Mod(1, y^2 + 7)*x^2 + Mod(1/2*y + 1/2, y^2 + 7)*x + Mod(-1, y^2 + 7), x^3 + Mod(1, y^2 + 7)*x + Mod(y, y^2 + 7))
vient du point trivial [Mod(1/2*y + 3/2, y^2 + 7), Mod(-y - 2, y^2 + 7), 1]
m1 = 1
m2 = 1
#S(E/K)[2] = 2
#E(K)/2E(K) = 2
#III(E/K)[2] = 1
rang(E/K) = 1
listpointsmwr = [[Mod(1/2*y + 3/2, y^2 + 7), Mod(-y - 2, y^2 + 7), 1]]
v = [1, 1, [[Mod(1/2*y + 3/2, y^2 + 7), Mod(-y - 2, y^2 + 7)]]]
(1, 1, [(1/2*a + 3/2 : -a - 2 : 1)])
A curve with 2-torsion:
sage: K.<a> = NumberField(x^2 + 7, 'a')
sage: E = EllipticCurve(K, '15a')
sage: v = E.simon_two_descent(); v # long time (about 10 seconds), points can vary
(1, 3, [...])
Returns the Tamagawa index of this elliptic curve at the prime  .
.
INPUT:
OUTPUT:
(positive integer) The Tamagawa index of the curve at P.
EXAMPLES:
sage: K.<a>=NumberField(x^2-5)
sage: E=EllipticCurve([20, 225, 750, 625*a + 6875, 31250*a + 46875])
sage: [E.tamagawa_exponent(P) for P in E.discriminant().support()]
[1, 1, 1, 1]
sage: K.<a> = QuadraticField(-11)
sage: E = EllipticCurve('11a1').change_ring(K)
sage: [E.tamagawa_exponent(P) for P in K(11).support()]
[10]
Returns the Tamagawa number of this elliptic curve at the prime  .
.
INPUT:
OUTPUT:
(positive integer) The Tamagawa number of the curve at  .
.
EXAMPLES:
sage: K.<a>=NumberField(x^2-5)
sage: E=EllipticCurve([20, 225, 750, 625*a + 6875, 31250*a + 46875])
sage: [E.tamagawa_number(P) for P in E.discriminant().support()]
[1, 1, 1, 1]
sage: K.<a> = QuadraticField(-11)
sage: E = EllipticCurve('11a1').change_ring(K)
sage: [E.tamagawa_number(P) for P in K(11).support()]
[10]
Given an elliptic curve  over a number field
over a number field  , this function returns the
integer
, this function returns the
integer 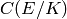 that appears in the Birch and Swinnerton-Dyer conjecture accounting
for the local information at finite places. If the model is a global minimal model then
that appears in the Birch and Swinnerton-Dyer conjecture accounting
for the local information at finite places. If the model is a global minimal model then 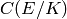 is
simply the product of the Tamagawa numbers
is
simply the product of the Tamagawa numbers 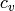 where
where  runs over all prime ideals of
runs over all prime ideals of  . Otherwise, if the model has to be changed at a place
. Otherwise, if the model has to be changed at a place  a correction factor appears.
The definition is such that
a correction factor appears.
The definition is such that 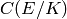 times the periods at the infinite places is invariant
under change of the Weierstrass model. See [Ta2] and [Do] for details.
times the periods at the infinite places is invariant
under change of the Weierstrass model. See [Ta2] and [Do] for details.
Note
This definition is slightly different from the definition of tamagawa_product
for curves defined over  . Over the rational number it is always defined to be the product
of the Tamagawa numbers, so the two definitions only agree when the model is global minimal.
. Over the rational number it is always defined to be the product
of the Tamagawa numbers, so the two definitions only agree when the model is global minimal.
OUTPUT:
A rational number
EXAMPLES:
sage: K.<i> = NumberField(x^2+1)
sage: E = EllipticCurve([0,2+i])
sage: E.tamagawa_product_bsd()
1
sage: E = EllipticCurve([(2*i+1)^2,i*(2*i+1)^7])
sage: E.tamagawa_product_bsd()
4
An example where the Neron model changes over K:
sage: K.<t> = NumberField(x^5-10*x^3+5*x^2+10*x+1)
sage: E = EllipticCurve(K,'75a1')
sage: E.tamagawa_product_bsd()
5
sage: da = E.local_data()
sage: [dav.tamagawa_number() for dav in da]
[1, 1]
REFERENCES:
Returns the order of the torsion subgroup of this elliptic curve.
OUTPUT:
(integer) the order of the torsion subgroup of this elliptic curve.
EXAMPLES:
sage: E = EllipticCurve('11a1')
sage: K.<t> = NumberField(x^4 + x^3 + 11*x^2 + 41*x + 101)
sage: EK = E.base_extend(K)
sage: EK.torsion_order()
25
sage: E = EllipticCurve('15a1')
sage: K.<t> = NumberField(x^2 + 2*x + 10)
sage: EK = E.base_extend(K)
sage: EK.torsion_order()
16
sage: E = EllipticCurve('19a1')
sage: K.<t> = NumberField(x^9-3*x^8-4*x^7+16*x^6-3*x^5-21*x^4+5*x^3+7*x^2-7*x+1)
sage: EK = E.base_extend(K)
sage: EK.torsion_order()
9
sage: K.<i> = QuadraticField(-1)
sage: EK = EllipticCurve([0,0,0,i,i+3])
sage: EK.torsion_order()
1
Returns a list of the torsion points of this elliptic curve.
OUTPUT:
(list) A sorted list of the torsion points.
EXAMPLES:
sage: E = EllipticCurve('11a1')
sage: E.torsion_points()
[(0 : 1 : 0), (5 : -6 : 1), (5 : 5 : 1), (16 : -61 : 1), (16 : 60 : 1)]
sage: K.<t> = NumberField(x^4 + x^3 + 11*x^2 + 41*x + 101)
sage: EK = E.base_extend(K)
sage: EK.torsion_points()
[(t : 1/11*t^3 + 6/11*t^2 + 19/11*t + 48/11 : 1),
(1/11*t^3 - 5/11*t^2 + 19/11*t - 40/11 : -6/11*t^3 - 3/11*t^2 - 26/11*t - 321/11 : 1),
(1/11*t^3 - 5/11*t^2 + 19/11*t - 40/11 : 6/11*t^3 + 3/11*t^2 + 26/11*t + 310/11 : 1),
(t : -1/11*t^3 - 6/11*t^2 - 19/11*t - 59/11 : 1),
(16 : 60 : 1),
(-3/55*t^3 - 7/55*t^2 - 2/55*t - 133/55 : 6/55*t^3 + 3/55*t^2 + 25/11*t + 156/55 : 1),
(14/121*t^3 - 15/121*t^2 + 90/121*t + 232/121 : 16/121*t^3 - 69/121*t^2 + 293/121*t - 46/121 : 1),
(-26/121*t^3 + 20/121*t^2 - 219/121*t - 995/121 : -15/121*t^3 - 156/121*t^2 + 232/121*t - 2887/121 : 1),
(10/121*t^3 + 49/121*t^2 + 168/121*t + 73/121 : -32/121*t^3 - 60/121*t^2 + 261/121*t + 686/121 : 1),
(5 : 5 : 1),
(-9/121*t^3 - 21/121*t^2 - 127/121*t - 377/121 : -7/121*t^3 + 24/121*t^2 + 197/121*t + 16/121 : 1),
(3/55*t^3 + 7/55*t^2 + 2/55*t + 78/55 : 7/55*t^3 - 24/55*t^2 + 9/11*t + 17/55 : 1),
(-5/121*t^3 + 36/121*t^2 - 84/121*t + 24/121 : -34/121*t^3 + 27/121*t^2 - 305/121*t - 829/121 : 1),
(5/121*t^3 - 14/121*t^2 - 158/121*t - 453/121 : 49/121*t^3 + 129/121*t^2 + 315/121*t + 86/121 : 1),
(5 : -6 : 1),
(5/121*t^3 - 14/121*t^2 - 158/121*t - 453/121 : -49/121*t^3 - 129/121*t^2 - 315/121*t - 207/121 : 1),
(-5/121*t^3 + 36/121*t^2 - 84/121*t + 24/121 : 34/121*t^3 - 27/121*t^2 + 305/121*t + 708/121 : 1),
(3/55*t^3 + 7/55*t^2 + 2/55*t + 78/55 : -7/55*t^3 + 24/55*t^2 - 9/11*t - 72/55 : 1),
(-9/121*t^3 - 21/121*t^2 - 127/121*t - 377/121 : 7/121*t^3 - 24/121*t^2 - 197/121*t - 137/121 : 1),
(16 : -61 : 1),
(10/121*t^3 + 49/121*t^2 + 168/121*t + 73/121 : 32/121*t^3 + 60/121*t^2 - 261/121*t - 807/121 : 1),
(-26/121*t^3 + 20/121*t^2 - 219/121*t - 995/121 : 15/121*t^3 + 156/121*t^2 - 232/121*t + 2766/121 : 1),
(14/121*t^3 - 15/121*t^2 + 90/121*t + 232/121 : -16/121*t^3 + 69/121*t^2 - 293/121*t - 75/121 : 1),
(-3/55*t^3 - 7/55*t^2 - 2/55*t - 133/55 : -6/55*t^3 - 3/55*t^2 - 25/11*t - 211/55 : 1),
(0 : 1 : 0)]
sage: E = EllipticCurve('15a1')
sage: K.<t> = NumberField(x^2 + 2*x + 10)
sage: EK = E.base_extend(K)
sage: EK.torsion_points()
[(t : t - 5 : 1),
(-1 : 0 : 1),
(t : -2*t + 4 : 1),
(8 : 18 : 1),
(1/2 : 5/4*t + 1/2 : 1),
(-2 : 3 : 1),
(-7 : 5*t + 8 : 1),
(3 : -2 : 1),
(-t - 2 : 2*t + 8 : 1),
(-13/4 : 9/8 : 1),
(-t - 2 : -t - 7 : 1),
(8 : -27 : 1),
(-7 : -5*t - 2 : 1),
(-2 : -2 : 1),
(1/2 : -5/4*t - 2 : 1),
(0 : 1 : 0)]
sage: K.<i> = QuadraticField(-1)
sage: EK = EllipticCurve(K,[0,0,0,0,-1])
sage: EK.torsion_points ()
[(-2 : -3*i : 1),
(0 : -i : 1),
(1 : 0 : 1),
(0 : i : 1),
(-2 : 3*i : 1),
(0 : 1 : 0)]
Returns the torsion subgroup of this elliptic curve.
OUTPUT:
(EllipticCurveTorsionSubgroup) The EllipticCurveTorsionSubgroup associated to this elliptic curve.
EXAMPLES:
sage: E = EllipticCurve('11a1')
sage: K.<t>=NumberField(x^4 + x^3 + 11*x^2 + 41*x + 101)
sage: EK=E.base_extend(K)
sage: tor = EK.torsion_subgroup()
sage: tor
Torsion Subgroup isomorphic to Multiplicative Abelian Group isomorphic to C5 x C5 associated to the Elliptic Curve defined by y^2 + y = x^3 + (-1)*x^2 + (-10)*x + (-20) over Number Field in t with defining polynomial x^4 + x^3 + 11*x^2 + 41*x + 101
sage: tor.gens()
((16 : 60 : 1), (t : 1/11*t^3 + 6/11*t^2 + 19/11*t + 48/11 : 1))
sage: E = EllipticCurve('15a1')
sage: K.<t>=NumberField(x^2 + 2*x + 10)
sage: EK=E.base_extend(K)
sage: EK.torsion_subgroup()
Torsion Subgroup isomorphic to Multiplicative Abelian Group isomorphic to C4 x C4 associated to the Elliptic Curve defined by y^2 + x*y + y = x^3 + x^2 + (-10)*x + (-10) over Number Field in t with defining polynomial x^2 + 2*x + 10
sage: E = EllipticCurve('19a1')
sage: K.<t>=NumberField(x^9-3*x^8-4*x^7+16*x^6-3*x^5-21*x^4+5*x^3+7*x^2-7*x+1)
sage: EK=E.base_extend(K)
sage: EK.torsion_subgroup()
Torsion Subgroup isomorphic to Multiplicative Abelian Group isomorphic to C9 associated to the Elliptic Curve defined by y^2 + y = x^3 + x^2 + (-9)*x + (-15) over Number Field in t with defining polynomial x^9 - 3*x^8 - 4*x^7 + 16*x^6 - 3*x^5 - 21*x^4 + 5*x^3 + 7*x^2 - 7*x + 1
sage: K.<i> = QuadraticField(-1)
sage: EK = EllipticCurve([0,0,0,i,i+3])
sage: EK.torsion_subgroup ()
Torsion Subgroup isomorphic to Trivial Abelian Group associated to the Elliptic Curve defined by y^2 = x^3 + i*x + (i+3) over Number Field in i with defining polynomial x^2 + 1