Univariate Power Series Rings

EXAMPLES: Power series rings are constructed in the standard Sage fashion.

sage: R.<t> = PowerSeriesRing(QQ)
sage: R.random_element(6)
-4 - 1/2*t^2 - 1/95*t^3 + 1/2*t^4 - 12*t^5 + O(t^6)

The default precision is specified at construction, but does not bound the precision of created elements.

sage: R.<t> = PowerSeriesRing(QQ, default_prec=5)
sage: R.random_element(6)
1/2 - 1/4*t + 2/3*t^2 - 5/2*t^3 + 2/3*t^5 + O(t^6)

sage: S = R([1, 3, 5, 7]); S  # XXX + O(t^5)
1 + 3*t + 5*t^2 + 7*t^3

sage: S.truncate(3)
5*t^2 + 3*t + 1

sage: S.<w> = PowerSeriesRing(QQ)
sage: S.base_ring()
Rational Field

An iterated example:

sage: R.<t> = PowerSeriesRing(ZZ)
sage: S.<t2> = PowerSeriesRing(R)
sage: S
Power Series Ring in t2 over Power Series Ring in t over Integer Ring
sage: S.base_ring()
Power Series Ring in t over Integer Ring

We compute with power series over the symbolic ring.

sage: K.<t> = PowerSeriesRing(SR, 5)
sage: a, b, c = var('a,b,c')
sage: f = a + b*t + c*t^2 + O(t^3)
sage: f*f
a^2 + 2*a*b*t + (2*a*c + b^2)*t^2 + O(t^3)
sage: f = sqrt(2) + sqrt(3)*t + O(t^3)
sage: f^2
2 + 2*sqrt(2)*sqrt(3)*t + 3*t^2 + O(t^3)

Elements are first coerced to constants in base_ring, then coerced into the PowerSeriesRing:

sage: R.<t> = PowerSeriesRing(ZZ)
sage: f = Mod(2, 3) * t; (f, f.parent())
(2*t, Power Series Ring in t over Ring of integers modulo 3)

We make a sparse power series.

sage: R.<x> = PowerSeriesRing(QQ, sparse=True); R
Sparse Power Series Ring in x over Rational Field
sage: f = 1 + x^1000000
sage: g = f*f
sage: g.degree()
2000000

We make a sparse Laurent series from a power series generator:

sage: R.<t> = PowerSeriesRing(QQ, sparse=True)
sage: latex(-2/3*(1/t^3) + 1/t + 3/5*t^2 + O(t^5))
\frac{-\frac{2}{3}}{t^{3}} + \frac{1}{t} + \frac{3}{5}t^{2} + O(t^{5})
sage: S = parent(1/t); S
Sparse Laurent Series Ring in t over Rational Field    

AUTHORS:

• William Stein: the code
• Jeremy Cho (2006-05-17): some examples (above)

TESTS:

sage: R.<t> = PowerSeriesRing(QQ)
sage: R == loads(dumps(R))
True

sage: R.<x> = PowerSeriesRing(QQ, sparse=True)
sage: R == loads(dumps(R))
True

sage.rings.power_series_ring.PowerSeriesRing(base_ring, name=None, default_prec=20, names=None, sparse=False)

Create a power series ring.

INPUT:

• base_ring - a commutative ring
• name - name of the indeterminate
• default_prec - (default: 20) the default precision used if an exact object must be changed to an approximate object in order to do an arithmetic operation.
• sparse - (default: False) whether power series are represented as sparse objects.

There is a unique power series ring over each base ring with given variable name. Two power series over the same base ring with different variable names are not equal or isomorphic.

EXAMPLES:

sage: R = PowerSeriesRing(QQ, 'x'); R
Power Series Ring in x over Rational Field

sage: S = PowerSeriesRing(QQ, 'y'); S
Power Series Ring in y over Rational Field

sage: R = PowerSeriesRing(QQ, 10)
...
ValueError: first letter of variable name must be a letter

sage: S = PowerSeriesRing(QQ, 'x', default_prec = 15); S
Power Series Ring in x over Rational Field
sage: S.default_prec()
15

class sage.rings.power_series_ring.PowerSeriesRing_domain(base_ring, name=None, default_prec=20, sparse=False, use_lazy_mpoly_ring=False)

Bases: sage.rings.power_series_ring.PowerSeriesRing_generic, sage.rings.ring.IntegralDomain

class sage.rings.power_series_ring.PowerSeriesRing_generic(base_ring, name=None, default_prec=20, sparse=False, use_lazy_mpoly_ring=False)

Bases: sage.rings.ring.CommutativeRing, sage.structure.nonexact.Nonexact

A power series ring.

base_extend(R)

Returns the power series ring over R in the same variable as self, assuming there is a canonical coerce map from the base ring of self to R.

EXAMPLES:

sage: R.<T> = GF(7)[[]]; R
Power Series Ring in T over Finite Field of size 7
sage: R.change_ring(ZZ)
Power Series Ring in T over Integer Ring
sage: R.base_extend(ZZ)
...
TypeError: no base extension defined

change_ring(R)

Returns the power series ring over R in the same variable as self.

EXAMPLES:

sage: R.<T> = QQ[[]]; R
Power Series Ring in T over Rational Field
sage: R.change_ring(GF(7))
Power Series Ring in T over Finite Field of size 7
sage: R.base_extend(GF(7))
...
TypeError: no base extension defined
sage: R.base_extend(QuadraticField(3,'a'))
Power Series Ring in T over Number Field in a with defining polynomial x^2 - 3

characteristic()

Return the characteristic of this power series ring, which is the same as the characteristic of the base ring of the power series ring.

EXAMPLES:

sage: R.<t> = PowerSeriesRing(ZZ)
sage: R.characteristic()
0
sage: R.<w> = Integers(2^50)[[]]; R
Power Series Ring in w over Ring of integers modulo 1125899906842624
sage: R.characteristic()
1125899906842624

construction()

Returns the functorial construction of self, namely, completion of the univariate polynomial ring with respect to the indeterminate (to a given precision).

EXAMPLE:

sage: R = PowerSeriesRing(ZZ, 'x')
sage: c, S = R.construction(); S
Univariate Polynomial Ring in x over Integer Ring
sage: R == c(S)
True

gen(n=0)

Return the generator of this power series ring.

EXAMPLES:

sage: R.<t> = PowerSeriesRing(ZZ)
sage: R.gen()
t
sage: R.gen(3)
...
IndexError: generator n>0 not defined

is_atomic_repr()

Return False since power objects do not appear atomically, i.e., they have plus and spaces.

is_dense()

is_exact()

is_field(proof=True)

Return False since the ring of power series over any ring is never a field.

is_finite()

Return False since the ring of power series over any ring is never finite.

EXAMPLES:

sage: R.<t> = PowerSeriesRing(ZZ)
sage: R.is_finite()
False

is_sparse()

laurent_series_ring()

If this is the power series ring , this function returns the Laurent series ring .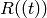

EXAMPLES:

sage: R.<t> = PowerSeriesRing(ZZ)
sage: R.laurent_series_ring()
Laurent Series Ring in t over Integer Ring

ngens()

Return the number of generators of this power series ring.

This is always 1.

EXAMPLES:

sage: R.<t> = ZZ[[]]
sage: R.ngens()
1

random_element(prec, bound=None)

Return a random power series.

INPUT:

• prec - an integer
• bound - an integer (default: None, which tries to spread choice across ring, if implemented)

OUTPUT:

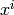• power series - a power series such that the coefficient of , for up to degree, are coercions to the base ring of random integers between -bound and bound.

IMPLEMENTATION: Call the random_element method on the underlying polynomial ring.

EXAMPLES:

sage: R.<t> = PowerSeriesRing(QQ)
sage: R.random_element(5)
-4 - 1/2*t^2 - 1/95*t^3 + 1/2*t^4 + O(t^5)
sage: R.random_element(5,20)
1/15 + 19/17*t + 10/3*t^2 + 5/2*t^3 + 1/2*t^4 + O(t^5)

variable_names_recursive(depth=None)

Returns the list of variable names of this and its base rings.

EXAMPLES:

sage: R = QQ[['x']][['y']][['z']]
sage: R.variable_names_recursive()
('x', 'y', 'z')
sage: R.variable_names_recursive(2)
('y', 'z')

class sage.rings.power_series_ring.PowerSeriesRing_over_field(base_ring, name=None, default_prec=20, sparse=False, use_lazy_mpoly_ring=False)

Bases: sage.rings.power_series_ring.PowerSeriesRing_domain

fraction_field()

Return the fraction field of this power series ring, which is defined since this is over a field.

This fraction field is just the Laurent series ring over the base field.

EXAMPLES:

sage: R.<t> = PowerSeriesRing(GF(7))
sage: R.fraction_field()
Laurent Series Ring in t over Finite Field of size 7
sage: Frac(R)
Laurent Series Ring in t over Finite Field of size 7

sage.rings.power_series_ring.is_PowerSeriesRing(R)

Return True if R is a power series ring.

EXAMPLES:

sage: from sage.rings.power_series_ring import is_PowerSeriesRing
sage: is_PowerSeriesRing(10)
False
sage: is_PowerSeriesRing(QQ[['x']])
True

sage.rings.power_series_ring.unpickle_power_series_ring_v0(base_ring, name, default_prec, sparse)