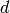Educational version of the $d$ -Groebner Basis Algorithm over PIDs.¶

No attempt was made to optimize this algorithm as the emphasis of this implementation is a clean and easy presentation.

Note

The notion of ‘term’ and ‘monomial’ in [BW93] is swapped from the notion of those words in Sage (or the other way around, however you prefer it). In Sage a term is a monomial multiplied by a coefficient, while in [BW93] a monomial is a term multiplied by a coefficient. Also, what is called LM (the leading monomial) in Sage is called HT (the head term) in [BW93].

EXAMPLE:

sage: from sage.rings.polynomial.toy_d_basis import d_basis

First, consider an example from arithmetic geometry:

sage: A.<x,y> = PolynomialRing(ZZ, 2)
sage: B.<X,Y> = PolynomialRing(Rationals(),2)
sage: f = -y^2 - y + x^3 + 7*x + 1
sage: fx = f.derivative(x)
sage: fy = f.derivative(y)
sage: I = B.ideal([B(f),B(fx),B(fy)])
sage: I.groebner_basis()
[1]

Since the output is 1, we know that there are no generic singularities.

To look at the singularities of the arithmetic surface, we need to do the corresponding computation over $\ZZ$ :

sage: I = A.ideal([f,fx,fy])
sage: gb = d_basis(I); gb
[x - 2020, y - 11313, 22627]

sage: gb[-1].factor()
11^3 * 17

This Groebner Basis gives a lot of information. First, the only fibers (over $\ZZ$ ) that are not smooth are at 11 = 0, and 17 = 0. Examining the Groebner Basis, we see that we have a simple node in both the fiber at 11 and at 17. From the factorization, we see that the node at 17 is regular on the surface (an $I_1$ node), but the node at 11 is not. 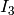After blowing up this non-regular point, we find that it is an $I_3$ node.

Another example. This one is from the Magma Handbook:

sage: P.<x, y, z> = PolynomialRing(IntegerRing(), 3, order='lex')
sage: I = ideal( x^2 - 1, y^2 - 1, 2*x*y - z)
sage: I = Ideal(d_basis(I))
sage: x.reduce(I)
x
sage: (2*x).reduce(I)
y*z

To compute modulo 4, we can add the generator 4 to our basis.:

sage: I = ideal( x^2 - 1, y^2 - 1, 2*x*y - z, 4)
sage: gb = d_basis(I)
sage: R = P.change_ring(IntegerModRing(4))
sage: gb = [R(f) for f in gb if R(f)]; gb
[x^2 - 1, x*z + 2*y, 2*x - y*z, y^2 - 1, z^2, 2*z]

A third example is also from the Magma Handbook.

This example shows how one can use Groebner bases over the integers to find the primes modulo which a system of equations has a solution, when the system has no solutions over the rationals.

We first form a certain ideal $I$ in $\ZZ[x, y, z]$ , and note that the Groebner basis of $I$ over $\QQ$ contains 1, so there are no solutions over $\QQ$ or an algebraic closure of it (this is not surprising as there are 4 equations in 3 unknowns).:

sage: P.<x, y, z> = PolynomialRing(IntegerRing(), 3)
sage: I = ideal( x^2 - 3*y, y^3 - x*y, z^3 - x, x^4 - y*z + 1 )
sage: I.change_ring( P.change_ring( RationalField() ) ).groebner_basis()
[1]

However, when we compute the Groebner basis of I (defined over $\ZZ$ ), we note that there is a certain integer in the ideal which is not 1.:

sage: d_basis(I) # random -- waiting on upstream singular fixes at #6051
[x + 170269749119, y + 2149906854, z + ..., 282687803443]

Now for each prime $p$ dividing this integer 282687803443, the Groebner basis of I modulo $p$ will be non-trivial and will thus give a solution of the original system modulo $p$ .:

sage: factor(282687803443)
101 * 103 * 27173681

sage: I.change_ring( P.change_ring( GF(101) ) ).groebner_basis()
[x + 19, y + 48, z - 33]

sage: I.change_ring( P.change_ring( GF(103) ) ).groebner_basis()
[x + 39, y + 8, z - 18]

sage: I.change_ring( P.change_ring( GF(27173681) ) ).groebner_basis()
[x - 536027, y + 3186055, z + 10380032]

Of course, modulo any other prime the Groebner basis is trivial so there are no other solutions. For example:

sage: I.change_ring( P.change_ring( GF(3) ) ).groebner_basis()
[1]

AUTHOR:

Martin Albrecht (2008-08): initial version

sage.rings.polynomial.toy_d_basis.LC(f)¶

sage.rings.polynomial.toy_d_basis.LM(f)¶

sage.rings.polynomial.toy_d_basis.d_basis(F, strat=True)¶

Return the 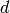$d$ -basis for the Ideal F as defined in [BW93].

INPUT:

F - an ideal
strat - use update strategy (default: True)

EXAMPLE:

sage: from sage.rings.polynomial.toy_d_basis import d_basis
sage: A.<x,y> = PolynomialRing(ZZ, 2)
sage: f = -y^2 - y + x^3 + 7*x + 1
sage: fx = f.derivative(x)
sage: fy = f.derivative(y)
sage: I = A.ideal([f,fx,fy])
sage: gb = d_basis(I); gb
[x - 2020, y - 11313, 22627]

sage.rings.polynomial.toy_d_basis.gpol(g1, g2)¶

Return G-Polynomial of g_1 and g_2.

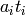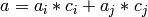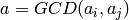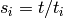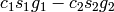Let $a_i t_i$ be $LT(g_i)$ , $a = a_i*c_i + a_j*c_j$ with $a = GCD(a_i,a_j)$ , and $s_i = t/t_i$ with $t = LCM(t_i,t_j)$ . Then the G-Polynomial is defined as: $c_1s_1g_1 - c_2s_2g_2$ .

INPUT:

g1 - polynomial
g2 - polynomial

EXAMPLE:

sage: from sage.rings.polynomial.toy_d_basis import gpol
sage: P.<x, y, z> = PolynomialRing(IntegerRing(), 3, order='lex')
sage: f = x^2 - 1
sage: g = 2*x*y - z
sage: gpol(f,g)
x^2*y - y

sage.rings.polynomial.toy_d_basis.select(P)¶

The normal selection strategy.

INPUT:

P - a list of critical pairs

OUTPUT:: an element of P

EXAMPLE:

sage: from sage.rings.polynomial.toy_d_basis import select
sage: A.<x,y> = PolynomialRing(ZZ, 2)
sage: f = -y^2 - y + x^3 + 7*x + 1
sage: fx = f.derivative(x)
sage: fy = f.derivative(y)
sage: G = [f, fx, fy]
sage: B = set(filter(lambda (x,y): x!=y, [(f1,f2) for f1 in G for f2 in G]))
sage: select(B)
(3*x^2 + 7, x^3 - y^2 + 7*x - y + 1)

sage.rings.polynomial.toy_d_basis.spol(g1, g2)¶

Return S-Polynomial of g_1 and g_2.

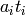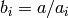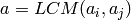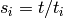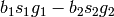Let $a_i t_i$ be $LT(g_i)$ , $b_i = a/a_i$ with $a = LCM(a_i,a_j)$ , and $s_i = t/t_i$ with $t = LCM(t_i,t_j)$ . Then the S-Polynomial is defined as: $b_1s_1g_1 - b_2s_2g_2$ .

INPUT:

g1 - polynomial
g2 - polynomial

EXAMPLE:

sage: from sage.rings.polynomial.toy_d_basis import spol
sage: P.<x, y, z> = PolynomialRing(IntegerRing(), 3, order='lex')
sage: f = x^2 - 1
sage: g = 2*x*y - z
sage: spol(f,g)
x*z - 2*y

sage.rings.polynomial.toy_d_basis.update(G, B, h)¶

Update G using the list of critical pairs B and the polynomial h as presented in [BW93], page 230. For this, Buchberger’s first and second criterion are tested.

This function uses the Gebauer-Moeller Installation.

INPUT:

G - an intermediate Groebner basis
B - a list of critical pairs
h - a polynomial

OUTPUT:: G,B where G and B are updated

EXAMPLE:

sage: from sage.rings.polynomial.toy_d_basis import update
sage: A.<x,y> = PolynomialRing(ZZ, 2)
sage: G = set([3*x^2 + 7, 2*y + 1, x^3 - y^2 + 7*x - y + 1])
sage: B = set([])
sage: h = x^2*y - x^2 + y - 3
sage: update(G,B,h)
(set([3*x^2 + 7, 2*y + 1, x^2*y - x^2 + y - 3, x^3 - y^2 + 7*x - y + 1]), 
 set([(x^2*y - x^2 + y - 3, x^3 - y^2 + 7*x - y + 1),  (x^2*y - x^2 + y - 3, 3*x^2 + 7), (x^2*y - x^2 + y - 3, 2*y + 1)]))

Educational version of the $d$ -Groebner Basis Algorithm over PIDs.¶

Previous topic

Next topic

This Page

Navigation

Educational version of the -Groebner Basis Algorithm over PIDs.¶

Previous topic

Next topic

This Page

Quick search

Navigation

Educational version of the $d$ -Groebner Basis Algorithm over PIDs.¶