Generic Convolution.

Asymptotically fast convolution of lists over any commutative ring in which the multiply-by-two map is injective. (More precisely, if 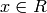, and 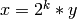for some 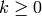, we require that 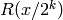returns .)

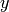The main function to be exported is convolution().

EXAMPLES:

sage: convolution([1, 2, 3, 4, 5], [6, 7])
[6, 19, 32, 45, 58, 35]

The convolution function is reasonably fast, even though it is written in pure Python. For example, the following takes less than a second:

sage: v=convolution(range(1000), range(1000))

ALGORITHM: Converts the problem to multiplication in the ring , where (where 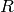is the original base ring). Performs FFT with respect to the roots of unity 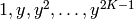in . The FFT/IFFT are accomplished with just additions and subtractions and rotating python lists. (I think this algorithm is essentially due to Schonhage, not completely sure.) The pointwise multiplications are handled recursively, switching to a classical algorithm at some point.

Complexity is O(n log(n) log(log(n))) additions/subtractions in R and O(n log(n)) multiplications in R.

AUTHORS:

• David Harvey (2007-07): first implementation
• William Stein: editing the docstrings for inclusion in Sage.

sage.rings.polynomial.convolution.convolution(L1, L2)

Returns convolution of non-empty lists L1 and L2. L1 and L2 may have arbitrary lengths.

EXAMPLES:

sage: convolution([1, 2, 3], [4, 5, 6, 7])
[4, 13, 28, 34, 32, 21]

sage: R = Integers(47)
sage: L1 = [R.random_element() for _ in range(1000)]
sage: L2 = [R.random_element() for _ in range(3756)]
sage: L3 = convolution(L1, L2)
sage: L3[2000] == sum([L1[i] * L2[2000-i] for i in range(1000)])
True
sage: len(L3) == 1000 + 3756 - 1
True