This module provides an implementation of ideals of polynomial rings in a countably infinite number of variables that are invariant under variable permutation. Such ideals are called ‘Symmetric Ideals’ in the rest of this document. Our implementation is based on the theory of M. Aschenbrenner and C. Hillar.
AUTHORS:
EXAMPLES:
Here, we demonstrate that working in quotient rings of Infinite Polynomial Rings works, provided that one uses symmetric Groebner bases.
sage: R.<x> = InfinitePolynomialRing(QQ)
sage: I = R.ideal([x[1]*x[2] + x[3]])
Note that I is not a symmetric Groebner basis:
sage: G = R*I.groebner_basis()
sage: G
Symmetric Ideal (x_1^2 + x_1, x_2 - x_1) of Infinite polynomial ring in x over Rational Field
sage: Q = R.quotient(G)
sage: p = x[3]*x[1]+x[2]^2+3
sage: Q(p)
-2*x_1 + 3
By the second generator of G, variable 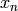 is equal to
is equal to 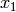 for any positive integer
for any positive integer  .
By the first generator of G,
.
By the first generator of G, 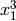 is equal to
is equal to 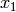 in Q. Indeed, we have
in Q. Indeed, we have
sage: Q(p)*x[2] == Q(p)*x[1]*x[3]*x[5]
True
Bases: sage.rings.ideal.Ideal_generic
Ideal in an Infinite Polynomial Ring, invariant under permutation of variable indices
THEORY:
An Infinite Polynomial Ring with finitely many generators 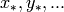 over
a field
over
a field  is a free commutative
is a free commutative  -algebra generated by infinitely many ‘variables’
-algebra generated by infinitely many ‘variables’
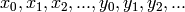 . We refer to the natural number
. We refer to the natural number  as the index
of the variable
as the index
of the variable 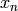 . See more detailed description at infinite_polynomial_ring
. See more detailed description at infinite_polynomial_ring
Infinite Polynomial Rings are equipped with a permutation action by permuting positive
variable indices, i.e., 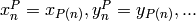 for any permutation
for any permutation 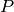 .
Note that the variables
.
Note that the variables 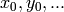 of index zero are invariant under that action.
of index zero are invariant under that action.
A Symmetric Ideal is an ideal in an infinite polynomial ring  that is invariant under
the permutation action. In other words, if
that is invariant under
the permutation action. In other words, if 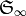 denotes the symmetric
group of
denotes the symmetric
group of 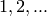 , then a Symmetric Ideal is a right
, then a Symmetric Ideal is a right ![X[\mathfrak S_\infty]](../../../_images/math/3cb1a1dcce536a509fc26db4f641e7aeb4444e0a.png) -submodule
of
-submodule
of  .
.
It is known by work of Aschenbrenner and Hillar [AB2007] that an Infinite Polynomial
Ring  with a single generator
with a single generator 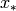 is Noetherian, in the sense
that any Symmetric Ideal
is Noetherian, in the sense
that any Symmetric Ideal 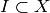 is finitely generated modulo addition,
multiplication by elements of
is finitely generated modulo addition,
multiplication by elements of  , and permutation of variable indices (hence, it is a
finitely generated right
, and permutation of variable indices (hence, it is a
finitely generated right ![X[\mathfrak S_\infty]](../../../_images/math/3cb1a1dcce536a509fc26db4f641e7aeb4444e0a.png) -module).
-module).
Moreover, if  is equipped with a lexicographic monomial ordering with
is equipped with a lexicographic monomial ordering with 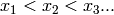 then there is an algorithm of Buchberger type that computes a Groebner basis
then there is an algorithm of Buchberger type that computes a Groebner basis  for
for 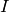 that allows for computation of a unique normal form, that is zero precisely for the elements
of
that allows for computation of a unique normal form, that is zero precisely for the elements
of 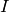 – see [AB2008]. See groebner_basis() for more details.
– see [AB2008]. See groebner_basis() for more details.
Our implementation allows more than one generator and also provides degree lexicographic and degree reverse lexicographic monomial orderings – we do, however, not guarantee termination of the Buchberger algorithm in these cases.
| [AB2007] | M. Aschenbrenner, C. Hillar, Finite generation of symmetric ideals. Trans. Amer. Math. Soc. 359 (2007), no. 11, 5171–5192. |
| [AB2008] | (1, 2, 3) M. Aschenbrenner, C. Hillar, An Algorithm for Finding Symmetric Groebner Bases in Infinite Dimensional Rings. |
EXAMPLES:
sage: X.<x,y> = InfinitePolynomialRing(QQ)
sage: I=X*(x[1]^2+y[2]^2,x[1]*x[2]*y[3]+x[1]*y[4])
sage: I == loads(dumps(I))
True
sage: latex(I)
\left(x_{1}^{2} + y_{2}^{2}, x_{2} x_{1} y_{3} + x_{1} y_{4}\right)\Bold{Q}[x_{\ast}, y_{\ast}][\mathfrak{S}_{\infty}]
The default ordering is lexicographic. We now compute a Groebner basis:
sage: J=I.groebner_basis() ; J # long time
[y_1^5 + y_1^3, y_2*y_1^2 - y_1^3, y_2^2 - y_1^2, x_1*y_1^2 - y_1^4, x_1*y_2 - y_1^3, x_1^2 + y_1^2, x_2*y_1 - y_1^3]
Ideal membership in I can now be tested by commuting symmetric reduction modulo J:
sage: I.reduce(J) # depends on long time example above
Symmetric Ideal (0, 0) of Infinite polynomial ring in x, y over Rational Field
Note that the Groebner basis is not point-wise invariant under permutation. However, any element of J has symmetric reduction zero even after applying a permutation:
sage: P=Permutation([1, 4, 3, 2])
sage: J[2] # depends on long time example above
y_2^2 - y_1^2
sage: J[2]^P # depends on long time example above
y_4^2 - y_1^2
sage: J.__contains__(J[2]^P) # depends on long time example above
False
sage: [[(p^P).reduce(J) for p in J] for P in Permutations(4)] # long time
[[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]]
Since I is not a Groebner basis, it is no surprise that it can not detect ideal membership:
sage: [p.reduce(I) for p in J] # depends on long time example above
[y_1^5 + y_1^3, y_2*y_1^2 - y_1^3, y_2^2 - y_1^2, x_1*y_1^2 - y_1^4, x_1*y_2 - y_1^3, -y_2^2 + y_1^2, x_2*y_1 - y_1^3]
Note that we give no guarantee that the computation of a symmetric Groebner basis will terminate in an order different from lexicographic.
When multiplying Symmetric Ideals or raising them to some integer power, the permutation action is taken into account, so that the product is indeed the product of ideals in the mathematical sense.
sage: I=X*(x[1])
sage: I*I
Symmetric Ideal (x_1^2, x_2*x_1) of Infinite polynomial ring in x, y over Rational Field
sage: I^3
Symmetric Ideal (x_1^3, x_2*x_1^2, x_2^2*x_1, x_3*x_2*x_1) of Infinite polynomial ring in x, y over Rational Field
sage: I*I == X*(x[1]^2)
False
Return a symmetric Groebner basis (type Sequence) of self.
INPUT:
The computation of symmetric Groebner bases also involves the computation of classical Groebner bases, i.e., of Groebner bases for ideals in polynomial rings with finitely many variables. For these computations, Sage provides the following ALGORITHMS:
If only a system is given - e.g. ‘magma’ - the default algorithm is chosen for that system.
Note
The Singular and libSingular versions of the respective algorithms are identical, but the former calls an external Singular process while the later calls a C function, i.e. the calling overhead is smaller.
EXAMPLES:
sage: X.<x,y> = InfinitePolynomialRing(QQ)
sage: I1 = X*(x[1]+x[2],x[1]*x[2])
sage: I1.groebner_basis()
[x_1]
sage: I2 = X*(y[1]^2*y[3]+y[1]*x[3])
sage: I2.groebner_basis()
[x_1*y_2 + y_2^2*y_1, x_2*y_1 + y_2*y_1^2]
Note that a symmetric Groebner basis of a principal ideal is not necessarily formed by a single polynomial.
When using the algorithm originally suggested by Aschenbrenner and Hillar, the result is the same, but the computation takes much longer:
sage: I2.groebner_basis(use_full_group=True)
[x_1*y_2 + y_2^2*y_1, x_2*y_1 + y_2*y_1^2]
Last, we demonstrate how the report on the progress of computations looks like:
sage: I1.groebner_basis(report=True, reduced=True)
Symmetric interreduction
[1/2] >
[2/2] : >
[1/2] >
[2/2] >
Symmetrise 2 polynomials at level 2
Apply permutations
>
>
Symmetric interreduction
[1/3] >
[2/3] >
[3/3] : >
-> 0
[1/2] >
[2/2] >
Symmetrisation done
Classical Groebner basis
-> 2 generators
Symmetric interreduction
[1/2] >
[2/2] >
Symmetrise 2 polynomials at level 3
Apply permutations
>
>
:>
::>
:>
::>
Symmetric interreduction
[1/4] >
[2/4] : >
-> 0
[3/4] :: >
-> 0
[4/4] : >
-> 0
[1/1] >
Apply permutations
:>
:>
:>
Symmetric interreduction
[1/1] >
Classical Groebner basis
-> 1 generators
Symmetric interreduction
[1/1] >
Symmetrise 1 polynomials at level 4
Apply permutations
>
:>
:>
>
:>
:>
Symmetric interreduction
[1/2] >
[2/2] : >
-> 0
[1/1] >
Symmetric interreduction
[1/1] >
[x_1]
The Aschenbrenner-Hillar algorithm is only guaranteed to work if the base ring is a field. So, we raise a TypeError if this is not the case:
sage: R.<x,y> = InfinitePolynomialRing(ZZ)
sage: I = R*[x[1]+x[2],y[1]]
sage: I.groebner_basis()
...
TypeError: The base ring (= Integer Ring) must be a field
TESTS:
In an earlier version, the following examples failed:
sage: X.<y,z> = InfinitePolynomialRing(GF(5),order='degrevlex')
sage: I = ['-2*y_0^2 + 2*z_0^2 + 1', '-y_0^2 + 2*y_0*z_0 - 2*z_0^2 - 2*z_0 - 1', 'y_0*z_0 + 2*z_0^2 - 2*z_0 - 1', 'y_0^2 + 2*y_0*z_0 - 2*z_0^2 + 2*z_0 - 2', '-y_0^2 - 2*y_0*z_0 - z_0^2 + y_0 - 1']*X
sage: I.groebner_basis()
[1]
sage: Y.<x,y> = InfinitePolynomialRing(GF(3), order='degrevlex', implementation='sparse')
sage: I = ['-y_3']*Y
sage: I.groebner_basis()
[y_1]
A fully symmetrically reduced generating set (type Sequence) of self.
This does essentially the same as interreduction() with the option ‘tailreduce’, but it returns a Sequence rather than a SymmetricIdeal.
EXAMPLES:
sage: X.<x> = InfinitePolynomialRing(QQ)
sage: I=X*(x[1]+x[2],x[1]*x[2])
sage: I.interreduced_basis()
[-x_1^2, x_2 + x_1]
Return symmetrically interreduced form of self
INPUT:
EXAMPLES:
sage: X.<x> = InfinitePolynomialRing(QQ)
sage: I=X*(x[1]+x[2],x[1]*x[2])
sage: I.interreduction()
Symmetric Ideal (-x_1^2, x_2 + x_1) of Infinite polynomial ring in x over Rational Field
Here, we show the report option:
sage: I.interreduction(report=True)
Symmetric interreduction
[1/2] >
[2/2] : >
[1/2] >
[2/2] T[1] >
>
Symmetric Ideal (-x_1^2, x_2 + x_1) of Infinite polynomial ring in x over Rational Field
[m/n] indicates that polynomial number m is considered and the total number of polynomials under consideration is n. ‘-> 0’ is printed if a zero reduction occurred. The rest of the report is as described in sage.rings.polynomial.symmetric_reduction.SymmetricReductionStrategy.reduce().
Last, we demonstrate the use of the optional parameter RStrat:
sage: from sage.rings.polynomial.symmetric_reduction import SymmetricReductionStrategy
sage: R = SymmetricReductionStrategy(X)
sage: R
Symmetric Reduction Strategy in Infinite polynomial ring in x over Rational Field
sage: I.interreduction(RStrat=R)
Symmetric Ideal (-x_1^2, x_2 + x_1) of Infinite polynomial ring in x over Rational Field
sage: R
Symmetric Reduction Strategy in Infinite polynomial ring in x over Rational Field, modulo
x_1^2,
x_2 + x_1
sage: R = SymmetricReductionStrategy(X,[x[1]^2])
sage: I.interreduction(RStrat=R)
Symmetric Ideal (x_2 + x_1) of Infinite polynomial ring in x over Rational Field
Answers whether self is a maximal ideal, under the assumption that self is defined by a symmetric Groebner basis.
NOTE:
It is not checked whether self is in fact a symmetric Groebner basis. A wrong answer can result if this assumption does not hold. A NotImplementedError is raised if the base ring is not a field, since symmetric Groebner bases are not implemented in this setting.
EXAMPLES:
sage: R.<x,y> = InfinitePolynomialRing(QQ)
sage: I = R.ideal([x[1]+y[2], x[2]-y[1]])
sage: I = R*I.groebner_basis()
sage: I
Symmetric Ideal (y_1, x_1) of Infinite polynomial ring in x, y over Rational Field
sage: I = R.ideal([x[1]+y[2], x[2]-y[1]])
sage: I.is_maximal()
False
The preciding answer is wrong, since it is not the case that 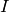 is given by a symmetric
Groebner basis:
is given by a symmetric
Groebner basis:
sage: I = R*I.groebner_basis()
sage: I
Symmetric Ideal (y_1, x_1) of Infinite polynomial ring in x, y over Rational Field
sage: I.is_maximal()
True
Return an ideal that coincides with self, so that all generators have leading coefficient 1.
Possibly occurring zeroes are removed from the generator list.
EXAMPLES:
sage: X.<x> = InfinitePolynomialRing(QQ)
sage: I = X*(1/2*x[1]+2/3*x[2], 0, 4/5*x[1]*x[2])
sage: I.normalisation()
Symmetric Ideal (x_2 + 3/4*x_1, x_2*x_1) of Infinite polynomial ring in x over Rational Field
Symmetric reduction of self by another Symmetric Ideal or list of Infinite Polynomials, or symmetric reduction of a given Infinite Polynomial by self.
INPUT:
Reducing an element  of an Infinite Polynomial Ring
of an Infinite Polynomial Ring  by some other element
by some other element  means the following:
means the following:
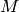 and
and 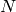 be the leading terms of
be the leading terms of  and
and  .
.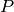 that does not does not diminish the variable
indices occurring in
that does not does not diminish the variable
indices occurring in 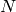 and preserves their order, so that there is some term
and preserves their order, so that there is some term 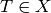 with
with 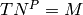 . If there is no such permutation, return
. If there is no such permutation, return 
 by
by 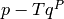 and continue with step 1.
and continue with step 1.EXAMPLES:
sage: X.<x,y> = InfinitePolynomialRing(QQ)
sage: I = X*(y[1]^2*y[3]+y[1]*x[3]^2)
sage: I.reduce([x[1]^2*y[2]])
Symmetric Ideal (x_3^2*y_1 + y_3*y_1^2) of Infinite polynomial ring in x, y over Rational Field
The preceding is correct, since any permutation that turns x[1]^2*y[2] into a factor of x[3]^2*y[2] interchanges the variable indices 1 and 2 – which is not allowed. However, reduction by x[2]^2*y[1] works, since one can change variable index 1 into 2 and 2 into 3:
sage: I.reduce([x[2]^2*y[1]])
Symmetric Ideal (y_3*y_1^2) of Infinite polynomial ring in x, y over Rational Field
The next example shows that tail reduction is not done, unless it is explicitly advised. The input can also be a symmetric ideal:
sage: J = (y[2])*X
sage: I.reduce(J)
Symmetric Ideal (x_3^2*y_1 + y_3*y_1^2) of Infinite polynomial ring in x, y over Rational Field
sage: I.reduce(J, tailreduce=True)
Symmetric Ideal (x_3^2*y_1) of Infinite polynomial ring in x, y over Rational Field
Reduce the variable indices occurring in self
EXAMPLES:
sage: X.<x,y> = InfinitePolynomialRing(QQ,implementation='sparse')
sage: I = X*(x[1000]*y[100],x[50]*y[1000])
sage: I.squeezed()
Symmetric Ideal (x_2*y_1, x_1*y_2) of Infinite polynomial ring in x, y over Rational Field
A symmetrised generating set (type Sequence) of self.
This does essentially the same as symmetrisation() with the option ‘tailreduce’, and it returns a Sequence rather than a SymmetricIdeal.
EXAMPLES:
sage: X.<x> = InfinitePolynomialRing(QQ)
sage: I = X*(x[1]+x[2], x[1]*x[2])
sage: I.symmetric_basis()
[x_1^2, x_2 + x_1]
Apply permutations to the generators of self and interreduce
INPUT:
EXAMPLES:
sage: X.<x> = InfinitePolynomialRing(QQ)
sage: I = X*(x[1]+x[2], x[1]*x[2])
sage: I.symmetrisation()
Symmetric Ideal (-x_1^2, x_2 + x_1) of Infinite polynomial ring in x over Rational Field
sage: I.symmetrisation(N=3)
Symmetric Ideal (-2*x_1) of Infinite polynomial ring in x over Rational Field
sage: I.symmetrisation(N=3, use_full_group=True)
Symmetric Ideal (-2*x_1) of Infinite polynomial ring in x over Rational Field