By Infinite Polynomial Rings, we mean polynomial rings in a countably infinite number of variables. The implementation consists of a wrapper around the current finite polynomial rings in Sage.
AUTHORS:
An Infinite Polynomial Ring has finitely many generators 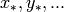 and infinitely many variables of the form
and infinitely many variables of the form 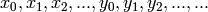 .
We refer to the natural number
.
We refer to the natural number  as the index of the variable
as the index of the variable 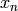 .
.
INPUT:
Each generator x produces an infinite sequence of variables x[1], x[2], ...
which are printed on screen as x_1, x_2, ... and are latex typeset as 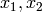 .
Then, the Infinite Polynomial Ring is formed by polynomials in these variables.
.
Then, the Infinite Polynomial Ring is formed by polynomials in these variables.
By default, the monomials are ordered lexicographically. Alternatively, degree (reverse) lexicographic ordering is possible as well. However, we do not guarantee that the computation of Groebner bases will terminate in this case.
In either case, the variables of a Infinite Polynomial Ring X are ordered according to the following rule:
X.gen(i)[m] > X.gen(j)[n] if and only if i<j or (i==j and m>n)
We provide a ‘dense’ and a ‘sparse’ implementation. In the dense implementation, the Infinite Polynomial Ring carries a finite polynomial ring that comprises all variables up to the maximal index that has been used so far. This is potentially a very big ring and may also comprise many variables that are not used.
In the sparse implementation, we try to keep the underlying finite polynomial rings small, using only those variables that are really needed. By default, we use the dense implementation, since it usually is much faster.
EXAMPLES:
sage: X.<x,y> = InfinitePolynomialRing(ZZ, implementation='sparse')
sage: A.<alpha,beta> = InfinitePolynomialRing(QQ, order='deglex')
sage: f = x[5] + 2; f
x_5 + 2
sage: g = 3*y[1]; g
3*y_1
It has some advantages to have an underlying ring that is not univariate. Hence, we always have at least two variables:
sage: g._p.parent()
Multivariate Polynomial Ring in y_1, y_0 over Integer Ring
sage: f2 = alpha[5] + 2; f2
alpha_5 + 2
sage: g2 = 3*beta[1]; g2
3*beta_1
sage: A.polynomial_ring()
Multivariate Polynomial Ring in alpha_5, alpha_4, alpha_3, alpha_2, alpha_1, alpha_0, beta_5, beta_4, beta_3, beta_2, beta_1, beta_0 over Rational Field
Of course, we provide the usual polynomial arithmetic:
sage: f+g
x_5 + 3*y_1 + 2
sage: p = x[10]^2*(f+g); p
x_10^2*x_5 + 3*x_10^2*y_1 + 2*x_10^2
sage: p2 = alpha[10]^2*(f2+g2); p2
alpha_10^2*alpha_5 + 3*alpha_10^2*beta_1 + 2*alpha_10^2
There is a permutation action on the variables, by permuting positive variable indices:
sage: P = Permutation(((10,1)))
sage: p^P
x_5*x_1^2 + 3*x_1^2*y_10 + 2*x_1^2
sage: p2^P
alpha_5*alpha_1^2 + 3*alpha_1^2*beta_10 + 2*alpha_1^2
Note that 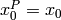 , since the permutations only change positive variable indices.
, since the permutations only change positive variable indices.
We also implemented ideals of Infinite Polynomial Rings. Here, it is thoroughly assumed that the ideals are set-wise invariant under the permutation action. We therefore refer to these ideals as Symmetric Ideals. Symmetric Ideals are finitely generated modulo addition, multiplication by ring elements and permutation of variables. If the base ring is a field, one can compute Symmetric Groebner Bases:
sage: J = A*(alpha[1]*beta[2])
sage: J.groebner_basis()
[alpha_1*beta_2, alpha_2*beta_1]
For more details, see SymmetricIdeal.
Infinite Polynomial Rings can have any commutative base ring. If the base ring of an Infinite Polynomial Ring is a (classical or infinite) Polynomial Ring, then our implementation tries to merge everything into one ring. The basic requirement is that the monomial orders match. In the case of two Infinite Polynomial Rings, the implementations must match. Moreover, name conflicts should be avoided. An overlap is only accepted if the order of variables can be uniquely inferred, as in the following example:
sage: A.<a,b,c> = InfinitePolynomialRing(ZZ)
sage: B.<b,c,d> = InfinitePolynomialRing(A)
sage: B
Infinite polynomial ring in a, b, c, d over Integer Ring
This is also allowed if finite polynomial rings are involved:
sage: A.<a_3,a_1,b_1,c_2,c_0> = ZZ[]
sage: B.<b,c,d> = InfinitePolynomialRing(A, order='degrevlex')
sage: B
Infinite polynomial ring in b, c, d over Multivariate Polynomial Ring in a_3, a_1 over Integer Ring
It is no problem if one generator of the Infinite Polynomial Ring is called x and one variable of the base ring is also called x. This is since no variable of the Infinite Polynomial Ring will be called x. However, a problem arises if the underlying classical Polynomial Ring has a variable x_1, since this can be confused with a variable of the Infinite Polynomial Ring. In this case, an error will be raised:
sage: X.<x,y_1> = ZZ[]
sage: Y.<x,z> = InfinitePolynomialRing(X)
Note that X is not merged into Y; this is since the monomial order of X is ‘degrevlex’, but of Y is ‘lex’.
sage: Y
Infinite polynomial ring in x, z over Multivariate Polynomial Ring in x, y_1 over Integer Ring
The variable x of X can still be interpreted in Y, although the first generator of Y is called x as well:
sage: x
x_*
sage: X('x')
x
sage: Y(X('x'))
x
sage: Y('x')
x
But there is only merging if the resulting monomial order is uniquely determined. This is not the case in the following examples, and thus an error is raised:
sage: X.<y_1,x> = ZZ[]
sage: Y.<y,z> = InfinitePolynomialRing(X)
...
CoercionException: Overlapping variables (('y', 'z'),['y_1']) are incompatible
sage: Y.<z,y> = InfinitePolynomialRing(X)
...
CoercionException: Overlapping variables (('z', 'y'),['y_1']) are incompatible
sage: X.<x_3,y_1,y_2> = PolynomialRing(ZZ,order='lex')
sage: # y_1 and y_2 would be in opposite order in an Infinite Polynomial Ring
sage: Y.<y> = InfinitePolynomialRing(X)
...
CoercionException: Overlapping variables (('y',),['y_1', 'y_2']) are incompatible
If the type of monomial orderings (e.g., ‘degrevlex’ versus ‘lex’) or if the implementations don’t match, there is no simplified construction available:
sage: X.<x,y> = InfinitePolynomialRing(ZZ)
sage: Y.<z> = InfinitePolynomialRing(X,order='degrevlex')
sage: Y
Infinite polynomial ring in z over Infinite polynomial ring in x, y over Integer Ring
sage: Y.<z> = InfinitePolynomialRing(X,implementation='sparse')
sage: Y
Infinite polynomial ring in z over Infinite polynomial ring in x, y over Integer Ring
TESTS:
Infinite Polynomial Rings are part of Sage’s coercion system. Hence, as long as the monomial orders and the implementations (dense versus sparse) are compatible, we can do arithmetic, so that the result lives in a ring into which all constituents coerce.
sage: R.<a,b> = InfinitePolynomialRing(ZZ)
sage: X.<x> = InfinitePolynomialRing(R)
sage: x[2]/2+(5/3)*a[3]*x[4] + 1
5/3*a_3*x_4 + 1/2*x_2 + 1
sage: R.<a,b> = InfinitePolynomialRing(ZZ,implementation='sparse')
sage: X.<x> = InfinitePolynomialRing(R)
sage: x[2]/2+(5/3)*a[3]*x[4] + 1
5/3*a_3*x_4 + 1/2*x_2 + 1
sage: R.<a,b> = InfinitePolynomialRing(ZZ,implementation='sparse')
sage: X.<x> = InfinitePolynomialRing(R,implementation='sparse')
sage: x[2]/2+(5/3)*a[3]*x[4] + 1
5/3*a_3*x_4 + 1/2*x_2 + 1
sage: R.<a,b> = InfinitePolynomialRing(ZZ)
sage: X.<x> = InfinitePolynomialRing(R,implementation='sparse')
sage: x[2]/2+(5/3)*a[3]*x[4] + 1
5/3*a_3*x_4 + 1/2*x_2 + 1
A dictionary-like class that is suitable for usage in sage_eval
EXAMPLES:
sage: R.<a,b> = InfinitePolynomialRing(ZZ)
sage: D = R.gens_dict() # indirect doc test
sage: D
GenDict of Infinite polynomial ring in a, b over Integer Ring
sage: D['a_15']
a_15
sage: type(_)
<class 'sage.rings.polynomial.infinite_polynomial_element.InfinitePolynomial_dense'>
sage: sage_eval('3*a_3*b_5-1/2*a_7', D)
-1/2*a_7 + 3*a_3*b_5
Return a dictionary that can be used to interprete strings in the base ring of self
EXAMPLES:
sage: R.<a,b> = InfinitePolynomialRing(QQ['t'])
sage: D = R.gens_dict()
sage: D
GenDict of Infinite polynomial ring in a, b over Univariate Polynomial Ring in t over Rational Field
sage: D.next()
GenDict of Univariate Polynomial Ring in t over Rational Field
sage: sage_eval('t^2',D.next())
t^2
A dictionary-like class that is suitable for usage in sage_eval
The generators of an Infinite Polynomial Ring are not variables. Variables of an Infinite Polynomial Ring are returned by indexing a generator. The purpose of this class is to return a variable of an Infinite Polynomial Ring, given its string representation.
EXAMPLES:
sage: R.<a,b> = InfinitePolynomialRing(ZZ)
sage: D = R.gens_dict() # indirect doc test
sage: D._D
[InfiniteGenDict defined by ['a', 'b'], {'1': 1}]
sage: D._D[0]['a_15']
a_15
sage: type(_)
<class 'sage.rings.polynomial.infinite_polynomial_element.InfinitePolynomial_dense'>
sage: sage_eval('3*a_3*b_5-1/2*a_7', D._D[0])
-1/2*a_7 + 3*a_3*b_5
Bases: sage.structure.sage_object.SageObject
This class provides the object which is responsible for returning variables in an infinite polynomial ring (implemented in __getitem__()).
EXAMPLES:
sage: X.<x1,x2> = InfinitePolynomialRing(RR)
sage: x1
x1_*
sage: x1[5]
x1_5
sage: x1 == loads(dumps(x1))
True
Bases: sage.structure.factory.UniqueFactory
A factory for creating infinite polynomial ring elements. It handles making sure that they are unique as well as handling pickling. For more details, see UniqueFactory and infinite_polynomial_ring.
EXAMPLES:
sage: A.<a> = InfinitePolynomialRing(QQ)
sage: B.<b> = InfinitePolynomialRing(A)
sage: B.construction()
[InfPoly{[a,b], "lex", "dense"}, Rational Field]
sage: R.<a,b> = InfinitePolynomialRing(QQ)
sage: R is B
True
sage: X.<x> = InfinitePolynomialRing(QQ)
sage: X2.<x> = InfinitePolynomialRing(QQ, implementation='sparse')
sage: X is X2
False
sage: X is loads(dumps(X))
True
Creates a key which uniquely defines the infinite polynomial ring.
TESTS:
sage: InfinitePolynomialRing.create_key(QQ, ('y1',))
(InfPoly{[y1], "lex", "dense"}(FractionField(...)), Integer Ring)
sage: _[0].all
[FractionField, InfPoly{[y1], "lex", "dense"}]
sage: InfinitePolynomialRing.create_key(QQ, names=['beta'], order='deglex', implementation='sparse')
(InfPoly{[beta], "deglex", "sparse"}(FractionField(...)), Integer Ring)
sage: _[0].all
[FractionField, InfPoly{[beta], "deglex", "sparse"}]
sage: InfinitePolynomialRing.create_key(QQ, names=['x','y'], implementation='dense')
(InfPoly{[x,y], "lex", "dense"}(FractionField(...)), Integer Ring)
sage: _[0].all
[FractionField, InfPoly{[x,y], "lex", "dense"}]
If no generator name is provided, a generator named ‘x’, lexicographic order and the dense implementation are assumed:
sage: InfinitePolynomialRing.create_key(QQ)
(InfPoly{[x], "lex", "dense"}(FractionField(...)), Integer Ring)
sage: _[0].all
[FractionField, InfPoly{[x], "lex", "dense"}]
If it is attempted to use no generator, a ValueError is raised:
sage: InfinitePolynomialRing.create_key(ZZ, names=[])
...
ValueError: Infinite Polynomial Rings must have at least one generator
Returns the infinite polynomial ring corresponding to the key key.
TESTS:
sage: InfinitePolynomialRing.create_object('1.0', InfinitePolynomialRing.create_key(ZZ, ('x3',)))
Infinite polynomial ring in x3 over Integer Ring
Bases: sage.rings.polynomial.infinite_polynomial_ring.InfinitePolynomialRing_sparse
Dense implementation of Infinite Polynomial Rings
Compared with InfinitePolynomialRing_sparse, from which this class inherits, it keeps a polynomial ring that comprises all elements that have been created so far.
Returns the underlying finite polynomial ring.
Note
This ring returned can change over time as more variables are used.
EXAMPLES:
sage: X.<x, y> = InfinitePolynomialRing(ZZ)
sage: X.polynomial_ring()
Multivariate Polynomial Ring in x_0, y_0 over Integer Ring
sage: a = y[3]
sage: X.polynomial_ring()
Multivariate Polynomial Ring in x_3, x_2, x_1, x_0, y_3, y_2, y_1, y_0 over Integer Ring
Return the tensor product of self with R
NOTE:
It is required that the underlying ring of self coerces into R.
EXAMPLES:
sage: R.<a,b> = InfinitePolynomialRing(ZZ, implementation='sparse')
sage: R.tensor_with_ring(QQ)
Infinite polynomial ring in a, b over Rational Field
sage: R
Infinite polynomial ring in a, b over Integer Ring
Bases: sage.rings.ring.CommutativeRing
Sparse implementation of Infinite Polynomial Rings.
An Infinite Polynomial Ring with generators 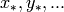 over a field
over a field
 is a free commutative
is a free commutative  -algebra generated by
-algebra generated by 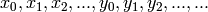 and is equipped with a permutation action
on the generators, namely
and is equipped with a permutation action
on the generators, namely 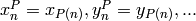 for any permutation
for any permutation 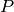 (note that variables of index zero are invariant
under such permutation).
(note that variables of index zero are invariant
under such permutation).
It is known that any permutation invariant ideal in an Infinite Polynomial Ring is finitely generated modulo the permutation action – see SymmetricIdeal for more details.
Usually, an instance of this class is created using InfinitePolynomialRing with the optional parameter implementation='sparse'. This takes care of uniqueness of parent structures. However, a direct construction is possible, in principle:
sage: X.<x,y> = InfinitePolynomialRing(QQ, implementation='sparse')
sage: Y.<x,y> = InfinitePolynomialRing(QQ, implementation='sparse')
sage: X is Y
True
sage: from sage.rings.polynomial.infinite_polynomial_ring import InfinitePolynomialRing_sparse
sage: Z = InfinitePolynomialRing_sparse(QQ, ['x','y'], 'lex')
sage: Z == X
True
sage: Z is X
False
The last parameter (‘lex’ in the above example) can also be ‘deglex’ or ‘degrevlex’; this would result in an Infinite Polynomial Ring in degree lexicographic or degree reverse lexicographic order.
See infinite_polynomial_ring for more details.
Return the characteristic of the base field.
EXAMPLES:
sage: X.<x,y> = InfinitePolynomialRing(GF(25,'a'))
sage: X
Infinite polynomial ring in x, y over Finite Field in a of size 5^2
sage: X.characteristic()
5
Returns the 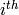 ‘generator’ (see the description in ngens())
of this infinite polynomial ring.
‘generator’ (see the description in ngens())
of this infinite polynomial ring.
EXAMPLES:
sage: X = InfinitePolynomialRing(QQ)
sage: x = X.gen()
sage: x[1]
x_1
sage: X.gen() is X.gen(0)
True
sage: XX = InfinitePolynomialRing(GF(5))
sage: XX.gen(0) is XX.gen()
True
Return False, since an infinite polynomial ring has at least one generator, hence, infinitely many variables.
EXAMPLES:
sage: R.<x, y> = InfinitePolynomialRing(QQ)
sage: R.is_field()
False
An infinite polynomial ring is an integral domain if and only if the base ring is.
EXAMPLES:
sage: R.<x, y> = InfinitePolynomialRing(QQ)
sage: R.is_integral_domain()
True
Return False, since polynomial rings in infinitely many variables are never Noetherian rings.
Note, however, that they are noetherian modules over the group ring of the symmetric group of the natural numbers
EXAMPLES:
sage: R.<x> = InfinitePolynomialRing(QQ)
sage: R.is_noetherian()
False
Return Infinity, since polynomial rings in infinitely many variables have infinite Krull dimension.
EXAMPLES:
sage: R.<x, y> = InfinitePolynomialRing(QQ)
sage: R.krull_dimension()
+Infinity
Returns the number of generators for this ring. Since there are countably infinitely many variables in this polynomial ring, by ‘generators’ we mean the number of infinite families of variables. See infinite_polynomial_ring for more details.
EXAMPLES:
sage: X.<x> = InfinitePolynomialRing(ZZ)
sage: X.ngens()
1
sage: X.<x1,x2> = InfinitePolynomialRing(QQ)
sage: X.ngens()
2
TESTS:
sage: X.<x,y> = InfinitePolynomialRing(QQ)
sage: X.one()
1
TESTS:
sage: X.<x,y> = InfinitePolynomialRing(QQ)
sage: X.one_element()
1
Return Infinity, since polynomial rings have infinitely many elements.
EXAMPLES:
sage: R.<x> = InfinitePolynomialRing(GF(2))
sage: R.order()
+Infinity
Return the tensor product of self with a ring R
NOTE:
It is required that the underlying ring of self coerces into R.
EXAMPLES:
sage: R.<a,b> = InfinitePolynomialRing(ZZ)
sage: R.tensor_with_ring(QQ)
Infinite polynomial ring in a, b over Rational Field
sage: R
Infinite polynomial ring in a, b over Integer Ring
Comparison of two variable names
INPUT:
RETURN:
-1,0,1 if x<y, x==y, x>y, respectively, where the order is defined as
follows: x<y 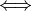 the string x.split('_')[0] is later in the list of
generator names of self than y.split('_')[0], or (x.split('_')[0]==y.split('_')[0] and
int(x.split('_')[1])<int(y.split('_')[1]))
the string x.split('_')[0] is later in the list of
generator names of self than y.split('_')[0], or (x.split('_')[0]==y.split('_')[0] and
int(x.split('_')[1])<int(y.split('_')[1]))
EXAMPLES:
sage: X.<alpha,beta> = InfinitePolynomialRing(ZZ)
sage: X.varname_cmp('alpha_1','beta_10')
1
sage: X.varname_cmp('beta_1','alpha_10')
-1
sage: X.varname_cmp('alpha_1','alpha_10')
-1
TESTS:
sage: X.<x,y> = InfinitePolynomialRing(QQ)
sage: X.zero()
0
TESTS:
sage: X.<x,y> = InfinitePolynomialRing(QQ)
sage: X.zero_element()
0