Navigation

Constructors for polynomial rings

This module provides the function PolynomialRing(), which constructs rings of univariate and multivariate polynomials, and implements caching to prevent the same ring being created in memory multiple times (which is wasteful).

There is also a function BooleanPolynomialRing_constructor(), used for constructing Boolean polynomial rings, which are not technically polynomial rings but rather quotients of them (see module sage.rings.polynomial.pbori for more details); and a deprecated constructor MPolynomialRing() (now subsumed by the generic PolynomialRing().

sage.rings.polynomial.polynomial_ring_constructor.BooleanPolynomialRing_constructor(n=None, names=None, order='lex')

Construct a boolean polynomial ring with the following parameters:

INPUT:

  • n – number of variables (an integer > 1)
  • names – names of ring variables, may be a string or list/tuple of strings
  • order – term order (default: lex)

EXAMPLES:

sage: R.<x, y, z> = BooleanPolynomialRing() # indirect doctest
sage: R
Boolean PolynomialRing in x, y, z

sage: p = x*y + x*z + y*z
sage: x*p
x*y*z + x*y + x*z

sage: R.term_order()
Lexicographic term order

sage: R = BooleanPolynomialRing(5,'x',order='deglex(3),deglex(2)')
sage: R.term_order()
deglex(3),deglex(2) term order

sage: R = BooleanPolynomialRing(3,'x',order='degrevlex')
sage: R.term_order()
Degree reverse lexicographic term order

sage: BooleanPolynomialRing(names=('x','y'))
Boolean PolynomialRing in x, y

sage: BooleanPolynomialRing(names='x,y')
Boolean PolynomialRing in x, y

TESTS:

sage: P.<x,y> = BooleanPolynomialRing(2,order='degrevlex')
sage: x > y
True

sage: P.<x0, x1, x2, x3> = BooleanPolynomialRing(4,order='degrevlex(2),degrevlex(2)')
sage: x0 > x1
True
sage: x2 > x3
True
sage.rings.polynomial.polynomial_ring_constructor.MPolynomialRing(*args, **kwds)

This function is deprecated and will be removed in a future version of Sage. Please use PolynomialRing instead.

If you have questions regarding this function and its replacement, please send your comments to sage-support@googlegroups.com.

sage.rings.polynomial.polynomial_ring_constructor.PolynomialRing(base_ring, arg1=None, arg2=None, sparse=False, order='degrevlex', names=None, name=None, implementation=None)

Return the globally unique univariate or multivariate polynomial ring with given properties and variable name or names.

There are four ways to call the polynomial ring constructor:

  1. PolynomialRing(base_ring, name,    sparse=False)
  2. PolynomialRing(base_ring, names,   order='degrevlex')
  3. PolynomialRing(base_ring, name, n, order='degrevlex')
  4. PolynomialRing(base_ring, n, name, order='degrevlex')

The optional arguments sparse and order must be explicitly named, and the other arguments must be given positionally.

INPUT:

  • base_ring – a commutative ring
  • name – a string
  • names – a list or tuple of names, or a comma separated string
  • n – an integer
  • sparse – bool (default: False), whether or not elements are sparse
  • order – string or TermOrder object, e.g.,
    • 'degrevlex' (default) – degree reverse lexicographic
    • 'lex' – lexicographic
    • 'deglex' – degree lexicographic
    • TermOrder('deglex',3) + TermOrder('deglex',3) – block ordering
  • implementation – string or None; selects an implementation in cases where Sage includes multiple choices (currently \ZZ[x] can be implemented with ‘NTL’ or ‘FLINT’; default is ‘FLINT’)

OUTPUT:

PolynomialRing(base_ring, name, sparse=False) returns a univariate polynomial ring; also, PolynomialRing(base_ring, names, sparse=False) yields a univariate polynomial ring, if names is a list or tuple providing exactly one name. All other input formats return a multivariate polynomial ring.

UNIQUENESS and IMMUTABILITY: In Sage there is exactly one single-variate polynomial ring over each base ring in each choice of variable, sparseness, and implementation. There is also exactly one multivariate polynomial ring over each base ring for each choice of names of variables and term order. The names of the generators can only be temporarily changed after the ring has been created. Do this using the localvars context:

EXAMPLES of VARIABLE NAME CONTEXT:

sage: R.<x,y> = PolynomialRing(QQ,2); R
Multivariate Polynomial Ring in x, y over Rational Field
sage: f = x^2 - 2*y^2

You can’t just globally change the names of those variables. This is because objects all over Sage could have pointers to that polynomial ring.

sage: R._assign_names(['z','w'])
...
ValueError: variable names cannot be changed after object creation.

However, you can very easily change the names within a with block:

sage: with localvars(R, ['z','w']):
...     print f
...     
z^2 - 2*w^2

After the with block the names revert to what they were before.

sage: print f
x^2 - 2*y^2

SQUARE BRACKETS NOTATION: You can alternatively create a single or multivariate polynomial ring over a ring 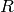R by writing R['varname'] or R['var1,var2,var3,...']. This square brackets notation doesn’t allow for setting any of the optional arguments.

EXAMPLES:

  1. PolynomialRing(base_ring, name,    sparse=False)

    sage: PolynomialRing(QQ, 'w')
Univariate Polynomial Ring in w over Rational Field

    Use the diamond brackets notation to make the variable ready for use after you define the ring:

    sage: R.<w> = PolynomialRing(QQ)
sage: (1 + w)^3
w^3 + 3*w^2 + 3*w + 1

    You must specify a name:

    sage: PolynomialRing(QQ)
...
TypeError: You must specify the names of the variables.

sage: R.<abc> = PolynomialRing(QQ, sparse=True); R
Sparse Univariate Polynomial Ring in abc over Rational Field

sage: R.<w> = PolynomialRing(PolynomialRing(GF(7),'k')); R
Univariate Polynomial Ring in w over Univariate Polynomial Ring in k over Finite Field of size 7

    The square bracket notation:

    sage: R.<y> = QQ['y']; R
Univariate Polynomial Ring in y over Rational Field
sage: y^2 + y
y^2 + y

    In fact, since the diamond brackets on the left determine the variable name, you can omit the variable from the square brackets:

    sage: R.<zz> = QQ[]; R
Univariate Polynomial Ring in zz over Rational Field
sage: (zz + 1)^2
zz^2 + 2*zz + 1

    This is exactly the same ring as what PolynomialRing returns:

    sage: R is PolynomialRing(QQ,'zz')
True

    However, rings with different variables are different:

    sage: QQ['x'] == QQ['y']
False

    Sage has two implementations of univariate polynomials over the integers, one based on NTL and one based on FLINT. The default is FLINT. Note that FLINT uses a “more dense” representation for its polynomials than NTL, so in particular, creating a polynomial like 2^1000000 * x^1000000 in FLINT may be unwise.

    sage: ZxNTL = PolynomialRing(ZZ, 'x', implementation='NTL'); ZxNTL
Univariate Polynomial Ring in x over Integer Ring (using NTL)
sage: ZxFLINT = PolynomialRing(ZZ, 'x', implementation='FLINT'); ZxFLINT
Univariate Polynomial Ring in x over Integer Ring
sage: ZxFLINT is ZZ['x']
True
sage: ZxFLINT is PolynomialRing(ZZ, 'x')
True
sage: xNTL = ZxNTL.gen()
sage: xFLINT = ZxFLINT.gen()
sage: xNTL.parent()
Univariate Polynomial Ring in x over Integer Ring (using NTL)
sage: xFLINT.parent()
Univariate Polynomial Ring in x over Integer Ring

    There is a coercion between the two rings, so the values can be mixed in a single expression.

    sage: (xNTL + xFLINT^2)
x^2 + x

    Unfortunately, it is unpredictable whether the result of such an expression will use the NTL or FLINT implementation.

    sage: (xNTL + xFLINT^2).parent()        # random output
Univariate Polynomial Ring in x over Integer Ring

  2. PolynomialRing(base_ring, names,   order='degrevlex')

    sage: R = PolynomialRing(QQ, 'a,b,c'); R
Multivariate Polynomial Ring in a, b, c over Rational Field

sage: S = PolynomialRing(QQ, ['a','b','c']); S
Multivariate Polynomial Ring in a, b, c over Rational Field

sage: T = PolynomialRing(QQ, ('a','b','c')); T
Multivariate Polynomial Ring in a, b, c over Rational Field

    All three rings are identical.

    sage: (R is S) and  (S is T)
True

    There is a unique polynomial ring with each term order:

    sage: R = PolynomialRing(QQ, 'x,y,z', order='degrevlex'); R
Multivariate Polynomial Ring in x, y, z over Rational Field
sage: S = PolynomialRing(QQ, 'x,y,z', order='invlex'); S
Multivariate Polynomial Ring in x, y, z over Rational Field
sage: S is PolynomialRing(QQ, 'x,y,z', order='invlex')
True
sage: R == S
False

    Note that a univariate polynomial ring is returned, if the list of names is of length one. If it is of length zero, a multivariate polynomial ring with no variables is returned.

    sage: PolynomialRing(QQ,["x"])
Univariate Polynomial Ring in x over Rational Field
sage: PolynomialRing(QQ,[])
Multivariate Polynomial Ring in no variables over Rational Field

  3. PolynomialRing(base_ring, name, n, order='degrevlex')

    If you specify a single name as a string and a number of variables, then variables labeled with numbers are created.

    sage: PolynomialRing(QQ, 'x', 10)
Multivariate Polynomial Ring in x0, x1, x2, x3, x4, x5, x6, x7, x8, x9 over Rational Field

sage: PolynomialRing(GF(7), 'y', 5)
Multivariate Polynomial Ring in y0, y1, y2, y3, y4 over Finite Field of size 7

sage: PolynomialRing(QQ, 'y', 3, sparse=True)
Multivariate Polynomial Ring in y0, y1, y2 over Rational Field

    Note that a multivariate polynomial ring is returned when an explicit number is given.

    sage: PolynomialRing(QQ,"x",1)
Multivariate Polynomial Ring in x over Rational Field
sage: PolynomialRing(QQ,"x",0)
Multivariate Polynomial Ring in no variables over Rational Field

    It is easy in Python to create fairly arbitrary variable names. For example, here is a ring with generators labeled by the first 100 primes:

    sage: R = PolynomialRing(ZZ, ['x%s'%p for p in primes(100)]); R
Multivariate Polynomial Ring in x2, x3, x5, x7, x11, x13, x17, x19, x23, x29, x31, x37, x41, x43, x47, x53, x59, x61, x67, x71, x73, x79, x83, x89, x97 over Integer Ring

    By calling the inject_variables() method, all those variable names are available for interactive use:

    sage: R.inject_variables()
Defining x2, x3, x5, x7, x11, x13, x17, x19, x23, x29, x31, x37, x41, x43, x47, x53, x59, x61, x67, x71, x73, x79, x83, x89, x97        
sage: (x2 + x41 + x71)^2
x2^2 + 2*x2*x41 + x41^2 + 2*x2*x71 + 2*x41*x71 + x71^2

Previous topic

Polynomial Rings

Next topic

Univariate Polynomials and Polynomial Rings

This Page

Navigation

© Copyright 2005--2010, The Sage Development Team. Created using Sphinx 0.6.3.