Term Orderings¶

Sage supports the following term orderings:

Lexicographic (lex)

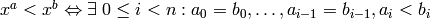
$x^a < x^b \Leftrightarrow \exists\; 0 \le i < n : a_0 = b_0, \ldots, a_{i-1} = b_{i-1}, a_i < b_i$

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQ, 3, order='lex')
sage: x > y
True
sage: x > y^2
True
sage: x > 1
True
sage: x^1*y^2 > y^3*z^4
True
sage: x^3*y^2*z^4 < x^3*y^2*z^1
False

This term ordering is called ‘lp’ in Singular.

Degree reverse lexicographic (degrevlex)

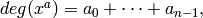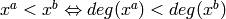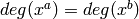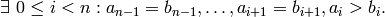
Let $deg(x^a) = a_0 + \cdots + a_{n-1},$ then $x^a < x^b \Leftrightarrow deg(x^a) < deg(x^b)$ or $deg(x^a) = deg(x^b)$ and $\exists\ 0 \le i < n: a_{n-1} = b_{n-1}, \ldots, a_{i+1} = b_{i+1}, a_i > b_i.$

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQ, 3, order='degrevlex')
sage: x > y
True
sage: x > y^2*z
False
sage: x > 1
True
sage: x^1*y^5*z^2 > x^4*y^1*z^3
True
sage: x^2*y*z^2 > x*y^3*z
False

This term ordering is called ‘dp’ in Singular.

Degree lexicographic (deglex)

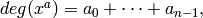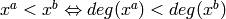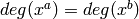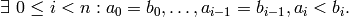
Let $deg(x^a) = a_0 + \cdots + a_{n-1},$ then $x^a < x^b \Leftrightarrow deg(x^a) < deg(x^b)$ or $deg(x^a) = deg(x^b)$ and $\exists\ 0 \le i < n:a_0 = b_0, \ldots, a_{i-1} = b_{i-1}, a_i < b_i.$

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQ, 3, order='deglex')
sage: x > y
True
sage: x > y^2*z
False
sage: x > 1
True
sage: x^1*y^2*z^3 > x^3*y^2*z^0
True
sage: x^2*y*z^2 > x*y^3*z
True

This term order is called ‘Dp’ in Singular.

Inverse lexicographic (invlex)

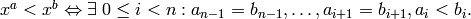
$x^a < x^b \Leftrightarrow \exists\; 0 \le i < n : a_{n-1} = b_{n-1}, \ldots, a_{i+1} = b_{i+1}, a_i < b_i.$

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQ, 3, order='invlex')
sage: x > y
False
sage: y > x^2
True
sage: x > 1
True
sage: x*y > z
False

This term ordering only makes sense in a non-commutative setting because if P is the ring $k[x_1, \dots, x_n]$ and term ordering ‘invlex’ then it is equivalent to the ring $k[x_n, \dots, x_1]$ with term ordering ‘lex’.

This ordering is called ‘rp’ in Singular.

Negative lexicographic (neglex)

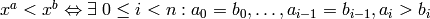
$x^a < x^b \Leftrightarrow \exists\; 0 \le i < n : a_0 = b_0, \ldots, a_{i-1} = b_{i-1}, a_i > b_i$

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQ, 3, order='neglex')
sage: x > y
False
sage: x > 1
False
sage: x^1*y^2 > y^3*z^4
False
sage: x^3*y^2*z^4 < x^3*y^2*z^1
True
sage: x*y > z
False

This term ordering is called ‘ls’ in Singular.

Negative degree reverse lexicographic (negdegrevlex)

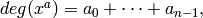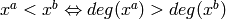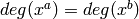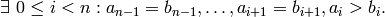
Let $deg(x^a) = a_0 + \cdots + a_{n-1},$ then $x^a < x^b \Leftrightarrow deg(x^a) > deg(x^b)$ or $deg(x^a) = deg(x^b)$ and $\exists\ 0 \le i < n: a_{n-1} = b_{n-1}, \ldots, a_{i+1} = b_{i+1}, a_i > b_i.$

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQ, 3, order='negdegrevlex')
sage: x > y
True
sage: x > x^2
True
sage: x > 1
False
sage: x^1*y^2 > y^3*z^4
True
sage: x^2*y*z^2 > x*y^3*z
False

This term ordering is called ‘ds’ in Singular.

Negative degree lexicographic (negdeglex)

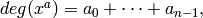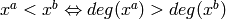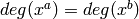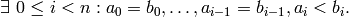
Let $deg(x^a) = a_0 + \cdots + a_{n-1},$ then $x^a < x^b \Leftrightarrow deg(x^a) > deg(x^b)$ or $deg(x^a) = deg(x^b)$ and $\exists\ 0 \le i < n: a_0 = b_0, \ldots, a_{i-1} = b_{i-1}, a_i < b_i.$

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQ, 3, order='negdeglex')
sage: x > y
True
sage: x > x^2
True
sage: x > 1
False
sage: x^1*y^2 > y^3*z^4
True
sage: x^2*y*z^2 > x*y^3*z
True

This term ordering is called ‘Ds’ in Singular.

Of these, only ‘degrevlex’, ‘deglex’, ‘invlex’ and ‘lex’ are global orderings.

Additionally all these monomial orderings may be combined to product or block orderings, defined as:

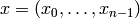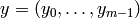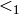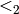Let $x = (x_0, \ldots, x_{n-1})$ and $y = (y_0, \ldots, y_{m-1})$ be two ordered sets of variables, $<_1$ a monomial ordering on $k[x]$ and $<_2$ a monomial ordering on $k[y]$ .

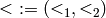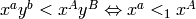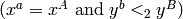The product ordering (or block ordering) $<\ := (<_1,<_2)$ on $k[x,y]$ is defined as: $x^a y^b < x^A y^B \Leftrightarrow x^a <_1 x^A$ or $(x^a =x^A \textrm{ and } y^b <_2 y^B)$ .

These block orderings are constructed in Sage by giving a comma separated list of monomial orderings with the length of each block attached to them.

EXAMPLE:

As an example, consider constructing a block ordering where the first four variables are compared using the degree reverse lexicographical ordering while the last two variables in the second block are compared using negative lexicographical ordering.

sage: P.<a,b,c,d,e,f> = PolynomialRing(QQ, 6,order='degrevlex(4),neglex(2)')
sage: a > c^4
False
sage: a > e^4
True
sage: e > f^2
False

The same result can be achieved by:

sage: T1 = TermOrder('degrevlex',4)
sage: T2 = TermOrder('neglex',2)
sage: T = T1 + T2
sage: P.<a,b,c,d,e,f> = PolynomialRing(QQ, 6, order=T)
sage: a > c^4
False
sage: a > e^4
True

If any other unsupported term ordering is given the provided string is passed through as is to Singular, Macaulay2, and Magma. This ensures that it is for example possible to calculate a Groebner basis with respect to some term ordering Singular supports but Sage doesn’t. However a warning is issued to make the user aware of the situation and potential typos:

sage: T = TermOrder("royalorder")
verbose 0 (...: term_order.py, __init__) Term ordering 'royalorder' unknown.

AUTHORS:

David Joyner and William Stein: initial version multi_polynomial_ring
Kiran S. Kedlaya: added macaulay2 interface
Martin Albrecht: implemented native term orderings, refactoring

class sage.rings.polynomial.term_order.TermOrder(name='lex', n=0, blocks=True, force=False)¶

Bases: sage.structure.sage_object.SageObject

A term order.

See sage.rings.polynomial.term_order for details on supported term orderings.

compare_tuples_Dp(f, g)¶

Compares two exponent tuples with respect to the degree lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQbar, 2, order='deglex')
sage: x > y^2 # indirect doctest
False
sage: x > 1
True

compare_tuples_Ds(f, g)¶

Compares two exponent tuples with respect to the negative degree lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQbar, 2, order='negdeglex')
sage: x > y^2 # indirect doctest
True
sage: x > 1
False

compare_tuples_block(f, g)¶

Compares two exponent tuples with respect to the block ordering as specified when constructing this element.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<a,b,c,d,e,f>=PolynomialRing(QQbar, 6, order='degrevlex(3),degrevlex(3)')
sage: a > c^4 # indirect doctest
False
sage: a > e^4
True

compare_tuples_dp(f, g)¶

Compares two exponent tuples with respect to the degree reversed lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQbar, 2, order='degrevlex')
sage: x > y^2 # indirect doctest
False
sage: x > 1
True

compare_tuples_ds(f, g)¶

Compares two exponent tuples with respect to the negative degree reverse lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQbar, 2, order='negdegrevlex')
sage: x > y^2 # indirect doctest
True
sage: x > 1
False

compare_tuples_lp(f, g)¶

Compares two exponent tuples with respect to the lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQbar, 2, order='lex')
sage: x > y^2 # indirect doctest
True
sage: x > 1
True

compare_tuples_ls(f, g)¶

Compares two exponent tuples with respect to the negative lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQbar, 2, order='neglex')
sage: x > y^2 # indirect doctest
False
sage: x > 1
False

compare_tuples_rp(f, g)¶

Compares two exponent tuples with respect to the inversed lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<x,y> = PolynomialRing(QQbar, 2, order='invlex')
sage: x > y^2 # indirect doctest
False
sage: x > 1
True

greater_tuple_Dp(f, g)¶

Returns the greater exponent tuple with respect to the total degree lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<x,y,z> = PolynomialRing(QQbar, 3, order='deglex')
sage: f = x + y; f.lm() # indirect doctest
x
sage: f = x + y^2*z; f.lm()
y^2*z

This method is called by the lm/lc/lt methods of MPolynomial_polydict.

greater_tuple_Ds(f, g)¶

Returns the greater exponent tuple with respect to the negative degree lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<x,y,z> = PolynomialRing(QQbar, 3, order='negdeglex')
sage: f = x + y; f.lm() # indirect doctest
x
sage: f = x + x^2; f.lm()
x
sage: f = x^2*y*z^2 + x*y^3*z; f.lm()
x^2*y*z^2

This method is called by the lm/lc/lt methods of MPolynomial_polydict.

greater_tuple_block(f, g)¶

Returns the greater exponent tuple with respect to the block ordering as specified when constructing this element.

This method is called by the lm/lc/lt methods of MPolynomial_polydict.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<a,b,c,d,e,f>=PolynomialRing(QQbar, 6, order='degrevlex(3),degrevlex(3)')
sage: f = a + c^4; f.lm() # indirect doctest
c^4
sage: g = a + e^4; g.lm()
a

greater_tuple_dp(f, g)¶

Returns the greater exponent tuple with respect to the total degree reversed lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQbar, 3, order='degrevlex')
sage: f = x + y; f.lm() # indirect doctest
x
sage: f = x + y^2*z; f.lm()
y^2*z

This method is called by the lm/lc/lt methods of MPolynomial_polydict.

greater_tuple_ds(f, g)¶

Returns the greater exponent tuple with respect to the negative degree reverse lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<x,y,z> = PolynomialRing(QQbar, 3, order='negdegrevlex')
sage: f = x + y; f.lm() # indirect doctest
x
sage: f = x + x^2; f.lm()
x
sage: f = x^2*y*z^2 + x*y^3*z; f.lm()
x*y^3*z

This method is called by the lm/lc/lt methods of MPolynomial_polydict.

greater_tuple_lp(f, g)¶

Returns the greater exponent tuple with respect to the lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLES:

sage: P.<x,y,z> = PolynomialRing(QQbar, 3, order='lex')
sage: f = x + y^2; f.lm() # indirect doctest
x

This method is called by the lm/lc/lt methods of MPolynomial_polydict.

greater_tuple_ls(f, g)¶

Returns the greater exponent tuple with respect to the negative lexicographical term order.

This method is called by the lm/lc/lt methods of MPolynomial_polydict.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<a,b,c,d,e,f>=PolynomialRing(QQbar, 6, order='degrevlex(3),degrevlex(3)')
sage: f = a + c^4; f.lm() # indirect doctest
c^4
sage: g = a + e^4; g.lm()
a

greater_tuple_rp(f, g)¶

Returns the greater exponent tuple with respect to the inversed lexicographical term order.

INPUT:

f - exponent tuple
g - exponent tuple

EXAMPLE:

sage: P.<x,y,z> = PolynomialRing(QQbar, 3, order='invlex')
sage: f = x + y; f.lm() # indirect doctest
y
sage: f = y + x^2; f.lm()
y

This method is called by the lm/lc/lt methods of MPolynomial_polydict.

is_global()¶

Return True if this term ordering is definitely global. Return False otherwise, which includes unknown term orderings.

EXAMPLE:

sage: T = TermOrder('lex')
sage: T.is_global()
True
sage: T = TermOrder('degrevlex', 3) + TermOrder('degrevlex', 3)
sage: T.is_global()
True
sage: T = TermOrder('degrevlex', 3) + TermOrder('negdegrevlex', 3)
sage: T.is_global()
False

is_local()¶

Return True if this term ordering is definitely local. Return False otherwise, which includes unknown term orderings.

EXAMPLE:

sage: T = TermOrder('lex')
sage: T.is_local()
False
sage: T = TermOrder('negdeglex', 3) + TermOrder('negdegrevlex', 3)
sage: T.is_local()
True
sage: T = TermOrder('degrevlex', 3) + TermOrder('negdegrevlex', 3)
sage: T.is_local()
False

macaulay2_str()¶

Return a Macaulay2 representation of self.

Used to convert polynomial rings to their Macaulay2 representation.

EXAMPLE:

sage: P = PolynomialRing(GF(127), 8,names='x',order='degrevlex(3),lex(5)')
sage: T = P.term_order()
sage: T.macaulay2_str()
'(GRevLex => 3,Lex => 5)'
sage: P._macaulay2_() # optional - macaulay2
ZZ/127 [x0, x1, x2, x3, x4, x5, x6, x7, MonomialOrder => {GRevLex => 3, Lex => 5}, MonomialSize => 16]

magma_str()¶

Return a MAGMA representation of self.

Used to convert polynomial rings to their MAGMA representation.

EXAMPLE:

sage: P = PolynomialRing(GF(127), 10,names='x',order='degrevlex')
sage: magma(P)                                                        # optional - magma
Polynomial ring of rank 10 over GF(127)
Graded Reverse Lexicographical Order
Variables: x0, x1, x2, x3, x4, x5, x6, x7, x8, x9

sage: T = P.term_order()
sage: T.magma_str()
'"grevlex"'

name()¶

EXAMPLE:

sage: TermOrder('lex').name()
'lex'

singular_str()¶

Return a SINGULAR representation of self.

Used to convert polynomial rings to their SINGULAR representation.

EXAMPLE:

sage: P = PolynomialRing(GF(127),10,names='x',order='lex(3),deglex(5),lex(2)')
sage: T = P.term_order()
sage: T.singular_str()
'(lp(3),Dp(5),lp(2))'
sage: P._singular_()
//   characteristic : 127
//   number of vars : 10
//        block   1 : ordering lp
//                  : names    x0 x1 x2
//        block   2 : ordering Dp
//                  : names    x3 x4 x5 x6 x7
//        block   3 : ordering lp
//                  : names    x8 x9
//        block   4 : ordering C

Term Orderings¶

Previous topic

Next topic

This Page

Navigation

Term Orderings¶

Previous topic

Next topic

This Page

Quick search

Navigation