Ring of Laurent Polynomials¶

If $R$ is a commutative ring, then the ring of Laurent polynomials in $n$ variables over $R$ is $R[x_1^{\pm 1}, x_2^{\pm 1}, \ldots, x_n^{\pm 1}]$ . We implement it as a quotient ring

$R[x_1, y_1, x_2, y_2, \ldots, x_n, y_n] / (x_1 y_1 - 1, x_2 y_2 - 1, \ldots, x_n y_n - 1).$

TESTS:

sage: P.<q> = LaurentPolynomialRing(QQ)
sage: qi = q^(-1)
sage: qi in P
True
sage: P(qi)
q^-1

sage: A.<Y> = QQ[]
sage: R.<X> = LaurentPolynomialRing(A)
sage: matrix(R,2,2,[X,0,0,1])
[X 0]
[0 1]

AUTHORS:

David Roe (2008-2-23): created
David Loeffler (2009-07-10): cleaned up docstrings

sage.rings.polynomial.laurent_polynomial_ring.LaurentPolynomialRing(base_ring, arg1=None, arg2=None, sparse=False, order='degrevlex', names=None, name=None)¶

Return the globally unique univariate or multivariate Laurent polynomial ring with given properties and variable name or names.

There are four ways to call the Laurent polynomial ring constructor:

LaurentPolynomialRing(base_ring, name, sparse=False)
LaurentPolynomialRing(base_ring, names, order='degrevlex')
LaurentPolynomialRing(base_ring, name, n, order='degrevlex')
LaurentPolynomialRing(base_ring, n, name, order='degrevlex')

The optional arguments sparse and order must be explicitly named, and the other arguments must be given positionally.

INPUT:

base_ring – a commutative ring
name – a string
names – a list or tuple of names, or a comma separated string
n – a positive integer
sparse – bool (default: False), whether or not elements are sparse
order – string or TermOrder, e.g.,
- 'degrevlex' (default) – degree reverse lexicographic
- 'lex' – lexicographic
- 'deglex' – degree lexicographic
- TermOrder('deglex',3) + TermOrder('deglex',3) – block ordering

OUTPUT:

LaurentPolynomialRing(base_ring, name, sparse=False) returns a univariate Laurent polynomial ring; all other input formats return a multivariate Laurent polynomial ring.

UNIQUENESS and IMMUTABILITY: In Sage there is exactly one single-variate Laurent polynomial ring over each base ring in each choice of variable and sparseness. There is also exactly one multivariate Laurent polynomial ring over each base ring for each choice of names of variables and term order.

sage: R.<x,y> = LaurentPolynomialRing(QQ,2); R
Multivariate Laurent Polynomial Ring in x, y over Rational Field
sage: f = x^2 - 2*y^-2

You can’t just globally change the names of those variables. This is because objects all over Sage could have pointers to that polynomial ring.

sage: R._assign_names(['z','w'])
...
ValueError: variable names cannot be changed after object creation.

EXAMPLES:

LaurentPolynomialRing(base_ring, name, sparse=False)

sage: LaurentPolynomialRing(QQ, 'w')
Univariate Laurent Polynomial Ring in w over Rational Field

Use the diamond brackets notation to make the variable ready for use after you define the ring:

sage: R.<w> = LaurentPolynomialRing(QQ)
sage: (1 + w)^3
w^3 + 3*w^2 + 3*w + 1

You must specify a name:

sage: LaurentPolynomialRing(QQ)
...
TypeError: You must specify the names of the variables.

sage: R.<abc> = LaurentPolynomialRing(QQ, sparse=True); R
Univariate Laurent Polynomial Ring in abc over Rational Field

sage: R.<w> = LaurentPolynomialRing(PolynomialRing(GF(7),'k')); R
Univariate Laurent Polynomial Ring in w over Univariate Polynomial Ring in k over Finite Field of size 7

Rings with different variables are different:

sage: LaurentPolynomialRing(QQ, 'x') == LaurentPolynomialRing(QQ, 'y')
False

LaurentPolynomialRing(base_ring, names, order='degrevlex')

sage: R = LaurentPolynomialRing(QQ, 'a,b,c'); R
Multivariate Laurent Polynomial Ring in a, b, c over Rational Field

sage: S = LaurentPolynomialRing(QQ, ['a','b','c']); S
Multivariate Laurent Polynomial Ring in a, b, c over Rational Field

sage: T = LaurentPolynomialRing(QQ, ('a','b','c')); T
Multivariate Laurent Polynomial Ring in a, b, c over Rational Field

All three rings are identical.

sage: (R is S) and  (S is T)
True

There is a unique Laurent polynomial ring with each term order:

sage: R = LaurentPolynomialRing(QQ, 'x,y,z', order='degrevlex'); R
Multivariate Laurent Polynomial Ring in x, y, z over Rational Field
sage: S = LaurentPolynomialRing(QQ, 'x,y,z', order='invlex'); S
Multivariate Laurent Polynomial Ring in x, y, z over Rational Field
sage: S is LaurentPolynomialRing(QQ, 'x,y,z', order='invlex')
True
sage: R == S
False

LaurentPolynomialRing(base_ring, name, n, order='degrevlex')

If you specify a single name as a string and a number of variables, then variables labeled with numbers are created.

sage: LaurentPolynomialRing(QQ, 'x', 10)
Multivariate Laurent Polynomial Ring in x0, x1, x2, x3, x4, x5, x6, x7, x8, x9 over Rational Field

sage: LaurentPolynomialRing(GF(7), 'y', 5)
Multivariate Laurent Polynomial Ring in y0, y1, y2, y3, y4 over Finite Field of size 7

sage: LaurentPolynomialRing(QQ, 'y', 3, sparse=True)
Multivariate Laurent Polynomial Ring in y0, y1, y2 over Rational Field

By calling the inject_variables() method, all those variable names are available for interactive use:

sage: R = LaurentPolynomialRing(GF(7),15,'w'); R
Multivariate Laurent Polynomial Ring in w0, w1, w2, w3, w4, w5, w6, w7, w8, w9, w10, w11, w12, w13, w14 over Finite Field of size 7        
sage: R.inject_variables()
Defining w0, w1, w2, w3, w4, w5, w6, w7, w8, w9, w10, w11, w12, w13, w14
sage: (w0 + 2*w8 + w13)^2
w0^2 + 4*w0*w8 + 4*w8^2 + 2*w0*w13 + 4*w8*w13 + w13^2

class sage.rings.polynomial.laurent_polynomial_ring.LaurentPolynomialRing_generic(R, prepend_string, names)¶

Bases: sage.rings.ring.CommutativeRing, sage.structure.parent_gens.ParentWithGens

change_ring(base_ring=None, names=None, sparse=False, order=None)¶

EXAMPLES:

sage: R = LaurentPolynomialRing(QQ,2,'x')
sage: R.change_ring(ZZ)
Multivariate Laurent Polynomial Ring in x0, x1 over Integer Ring

characteristic()¶

Returns the characteristic of the base ring.

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').characteristic()
0
sage: LaurentPolynomialRing(GF(3),2,'x').characteristic()
3

completion(p, prec=20, extras=None)¶

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').completion(3)
...
NotImplementedError

construction()¶

Returns the construction of self.

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x,y').construction()
(LaurentPolynomialFunctor,
Univariate Laurent Polynomial Ring in x over Rational Field)

gen(i=0)¶

Returns the 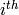$i^{th}$ generator of self. If i is not specified, then the first generator will be returned.

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').gen()
x0
sage: LaurentPolynomialRing(QQ,2,'x').gen(0)
x0
sage: LaurentPolynomialRing(QQ,2,'x').gen(1)
x1

TESTS:

sage: LaurentPolynomialRing(QQ,2,'x').gen(3)
...
ValueError: generator not defined

ideal()¶

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').ideal()
...
NotImplementedError

is_exact()¶

Returns True if the base ring is exact.

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').is_exact()
True
sage: LaurentPolynomialRing(RDF,2,'x').is_exact()
False

is_field(proof=True)¶

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').is_field()
False

is_finite()¶

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').is_finite()
False

is_integral_domain(proof=True)¶

Returns True if self is an integral domain.

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').is_integral_domain()
True

The following used to fail; see #7530:

sage: L = LaurentPolynomialRing(ZZ, 'X')
sage: L['Y']
Univariate Polynomial Ring in Y over Univariate Laurent Polynomial Ring in X over Integer Ring

is_noetherian()¶

Returns True if self is Noetherian.

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').is_noetherian()
...
NotImplementedError

krull_dimension()¶

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').krull_dimension()
...
NotImplementedError

ngens()¶

Returns the number of generators of self.

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').ngens()
2
sage: LaurentPolynomialRing(QQ,1,'x').ngens()
1

polynomial_ring()¶

Returns the polynomial ring associated with self.

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').polynomial_ring()
Multivariate Polynomial Ring in x0, x1 over Rational Field
sage: LaurentPolynomialRing(QQ,1,'x').polynomial_ring()
Multivariate Polynomial Ring in x over Rational Field

random_element(low_degree=-2, high_degree=2, terms=5, choose_degree=False, *args, **kwds)¶

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').random_element()
...
NotImplementedError

remove_var(var)¶

EXAMPLES:

sage: R = LaurentPolynomialRing(QQ,'x,y,z')
sage: R.remove_var('x')
Multivariate Laurent Polynomial Ring in y, z over Rational Field
sage: R.remove_var('x').remove_var('y')
Univariate Laurent Polynomial Ring in z over Rational Field

term_order()¶

Returns the term order of self.

EXAMPLES:

sage: LaurentPolynomialRing(QQ,2,'x').term_order()
Degree reverse lexicographic term order

class sage.rings.polynomial.laurent_polynomial_ring.LaurentPolynomialRing_mpair(R, prepend_string, names)¶: Bases: sage.rings.polynomial.laurent_polynomial_ring.LaurentPolynomialRing_generic

sage.rings.polynomial.laurent_polynomial_ring.is_LaurentPolynomialRing(R)¶

Returns True if and only if R is a Laurent polynomial ring.

EXAMPLES:

sage: from sage.rings.polynomial.laurent_polynomial_ring import is_LaurentPolynomialRing
sage: P = PolynomialRing(QQ,2,'x')
sage: is_LaurentPolynomialRing(P)
False

sage: R = LaurentPolynomialRing(QQ,3,'x')
sage: is_LaurentPolynomialRing(R)
True

Ring of Laurent Polynomials¶

Previous topic

Next topic

This Page

Navigation

Ring of Laurent Polynomials¶

Previous topic

Next topic

This Page

Quick search

Navigation