This module provides a function cyclotomic_coeffs(), which calculates the coefficients of cyclotomic polynomials. This is not intended to be invoked directly by the user, but it is called by the method cyclotomic_polynomial() method of univariate polynomial ring objects and the top-level cyclotomic_polynomial() function.
This calculates the coefficients of the n-th cyclotomic polynomial by using the formula
where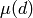 
is the Moebius function that is 1 if d has an even
number of distinct prime divisors, -1 if it has an odd number of
distinct prime divisors, and 0 if d is not squarefree.
Multiplications and divisions by polynomials of the
form 
can be done very quickly in a single pass.
If sparse is True, the result is returned as a dictionary of the non-zero entries, otherwise the result is returned as a list of python ints.
EXAMPLES:
sage: from sage.rings.polynomial.cyclotomic import cyclotomic_coeffs
sage: cyclotomic_coeffs(30)
[1, 1, 0, -1, -1, -1, 0, 1, 1]
sage: cyclotomic_coeffs(10^5)
{0: 1, 10000: -1, 40000: 1, 30000: -1, 20000: 1}
sage: R = QQ['x']
sage: R(cyclotomic_coeffs(30))
x^8 + x^7 - x^5 - x^4 - x^3 + x + 1
Check that it has the right degree:
sage: euler_phi(30)
8
sage: R(cyclotomic_coeffs(14)).factor()
x^6 - x^5 + x^4 - x^3 + x^2 - x + 1
The coefficients are not always +/-1:
sage: cyclotomic_coeffs(105)
[1, 1, 1, 0, 0, -1, -1, -2, -1, -1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, -1, 0, -1, 0, -1, 0, -1, 0, -1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, -1, -1, -2, -1, -1, 0, 0, 1, 1, 1]
In fact the height is not bounded by any polynomial in n (Erdos), although takes a while just to exceed linear:
sage: v = cyclotomic_coeffs(1181895)
sage: max(v)
14102773
The polynomial is a palindrome for any n:
sage: n = ZZ.random_element(50000)
sage: factor(n)
3 * 10009
sage: v = cyclotomic_coeffs(n, sparse=False)
sage: v == list(reversed(v))
True
AUTHORS: