-Adic Base Leaves.

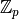Implementations of and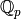

AUTHORS:

• David Roe
• Genya Zaytman: documentation
• David Harvey: doctests
• William Stein: doctest updates

EXAMPLES:

-Adic rings and fields are examples of inexact structures, as the reals are. That means that elements cannot generally be stored exactly: to do so would take an infinite amount of storage. Instead, we store an approximation to the elements with varying precision.

There are two types of precision for a -adic element. The first is relative precision, which gives the number of known -adic digits:

sage: R = Qp(5, 20, 'capped-rel', 'series'); a = R(675); a
2*5^2 + 5^4 + O(5^22)
sage: a.precision_relative()
20

The second type of precision is absolute precision, which gives the power of that this element is stored modulo:

sage: a.precision_absolute()
22

The number of times that divides the element is called the valuation, and can be accessed with the functions valuation() and ordp():

sage: a.valuation() 2

The following relationship holds:

self.valuation() + self.precision_relative() == self.precision_absolute().

sage: a.valuation() + a.precision_relative() == a.precision_absolute() True

In the capped relative case, the relative precision of an element is restricted to be at most a certain value, specified at the creation of the field. Individual elements also store their own precision, so the effect of various arithmetic operations on precision is tracked. When you cast an exact element into a capped relative field, it truncates it to the precision cap of the field.:

sage: R = Qp(5, 5); a = R(4006); a
1 + 5 + 2*5^3 + 5^4 + O(5^5)
sage: b = R(17/3); b
4 + 2*5 + 3*5^2 + 5^3 + 3*5^4 + O(5^5)
sage: c = R(4025); c
5^2 + 2*5^3 + 5^4 + 5^5 + O(5^7)
sage: a + b
4*5 + 3*5^2 + 3*5^3 + 4*5^4 + O(5^5)
sage: a + b + c
4*5 + 4*5^2 + 5^4 + O(5^5)

sage: R = Zp(5, 5, 'capped-rel', 'series'); a = R(4006); a
1 + 5 + 2*5^3 + 5^4 + O(5^5)
sage: b = R(17/3); b
4 + 2*5 + 3*5^2 + 5^3 + 3*5^4 + O(5^5)
sage: c = R(4025); c
5^2 + 2*5^3 + 5^4 + 5^5 + O(5^7)
sage: a + b
4*5 + 3*5^2 + 3*5^3 + 4*5^4 + O(5^5)
sage: a + b + c
4*5 + 4*5^2 + 5^4 + O(5^5)

In the capped absolute type, instead of having a cap on the relative precision of an element there is instead a cap on the absolute precision. Elements still store their own precisions, and as with the capped relative case, exact elements are truncated when cast into the ring.:

sage: R = ZpCA(5, 5); a = R(4005); a
5 + 2*5^3 + 5^4 + O(5^5)
sage: b = R(4025); b
5^2 + 2*5^3 + 5^4 + O(5^5)
sage: a * b
5^3 + 2*5^4 + O(5^5)
sage: (a * b) // 5^3
1 + 2*5 + O(5^2)
sage: type((a * b) // 5^3)
<type 'sage.rings.padics.padic_capped_absolute_element.pAdicCappedAbsoluteElement'>
sage: (a * b) / 5^3
1 + 2*5 + O(5^2)
sage: type((a * b) / 5^3)
<type 'sage.rings.padics.padic_capped_relative_element.pAdicCappedRelativeElement'>

The fixed modulus type is the leanest of the p-adic rings: it is basically just a wrapper around 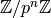providing a unified interface with the rest of the -adics. This is the type you should use if your primary interest is in speed (though it’s not all that much faster than other -adic types). It does not track precision of elements.:

sage: R = ZpFM(5, 5); a = R(4005); a
5 + 2*5^3 + 5^4 + O(5^5)
sage: a // 5
1 + 2*5^2 + 5^3 + O(5^5)

-Adic rings and fields should be created using the creation functions Zp and Qp as above. This will ensure that there is only one instance of 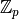and 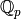of a given type, , print mode and precision. It also saves typing very long class names.:

sage: Qp(17,10)
17-adic Field with capped relative precision 10
sage: R = Qp(7, prec = 20, print_mode = 'val-unit'); S = Qp(7, prec = 20, print_mode = 'val-unit'); R is S
True
sage: Qp(2)
2-adic Field with capped relative precision 20

Once one has a -Adic ring or field, one can cast elements into it in the standard way. Integers, ints, longs, Rationals, other -Adic types, pari -adics and elements of 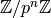can all be cast into a -Adic field.:

sage: R = Qp(5, 5, 'capped-rel','series'); a = R(16); a
1 + 3*5 + O(5^5)
sage: b = R(23/15); b
5^-1 + 3 + 3*5 + 5^2 + 3*5^3 + O(5^4)
sage: S = Zp(5, 5, 'fixed-mod','val-unit'); c = S(Mod(75,125)); c
5^2 * 3 + O(5^5)
sage: R(c)
3*5^2 + O(5^5)

In the previous example, since fixed-mod elements don’t keep track of their precision, we assume that it has the full precision of the ring. This is why you have to cast manually here.

While you can cast explicitly as above, the chains of automatic coercion are more restricted. As always in Sage, the following arrows are transitive and the diagram is commutative.:

int -> long -> Integer -> Zp capped-rel -> Zp capped_abs -> IntegerMod
Integer -> Zp fixed-mod -> IntegerMod
Integer -> Zp capped-abs -> Qp capped-rel

In addition, there are arrows within each type. For capped relative and capped absolute rings and fields, these arrows go from lower precision cap to higher precision cap. This works since elements track their own precision: choosing the parent with higher precision cap means that precision is less likely to be truncated unnecessarily. For fixed modulus parents, the arrow goes from higher precision cap to lower. The fact that elements do not track precision necessitates this choice in order to not produce incorrect results.

TESTS:

sage: R = Qp(5, 15, print_mode='bars', print_sep='&'); S = loads(dumps(R))
sage: R == S
True
sage: repr(S(2777))[3:]
'4&2&1&0&2'

sage: R = Zp(5, 15, print_mode='bars', print_sep='&'); S = loads(dumps(R))
sage: R == S
True
sage: repr(S(2777))[3:]
'4&2&1&0&2'

sage: R = ZpCA(5, 15, print_mode='bars', print_sep='&'); S = loads(dumps(R))
sage: R == S
True
sage: repr(S(2777))[3:]
'4&2&1&0&2'

class sage.rings.padics.padic_base_leaves.pAdicFieldCappedRelative(p, prec, print_mode, names)

Bases: sage.rings.padics.generic_nodes.pAdicFieldBaseGeneric, sage.rings.padics.generic_nodes.pAdicCappedRelativeFieldGeneric

An implementation of -adic fields with capped relative precision.

EXAMPLES:

sage: K = Qp(17, 1000000)
sage: K = Qp(next_prime(10^60))

random_element(algorithm='default')

Returns a random element of self, optionally using the algorithm argument to decide how it generates the element. Algorithms currently implemented:

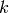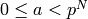• default: Choose an integer using the standard distribution on the integers. Then choose an integer uniformly in the range where 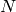is the precision cap of self. Return self(p^k * a, absprec = k + self.precision_cap()).

EXAMPLES:

sage: Qp(17,6).random_element()
15*17^-8 + 10*17^-7 + 3*17^-6 + 2*17^-5 + 11*17^-4 + 6*17^-3 + O(17^-2)

class sage.rings.padics.padic_base_leaves.pAdicRingCappedAbsolute(p, prec, print_mode, names)

Bases: sage.rings.padics.generic_nodes.pAdicRingBaseGeneric, sage.rings.padics.generic_nodes.pAdicCappedAbsoluteRingGeneric

An implementation of the -adic integers with capped absolute precision.

class sage.rings.padics.padic_base_leaves.pAdicRingCappedRelative(p, prec, print_mode, names)

Bases: sage.rings.padics.generic_nodes.pAdicRingBaseGeneric, sage.rings.padics.generic_nodes.pAdicCappedRelativeRingGeneric

An implementation of the -adic integers with capped relative precision.

class sage.rings.padics.padic_base_leaves.pAdicRingFixedMod(p, prec, print_mode, names)

Bases: sage.rings.padics.generic_nodes.pAdicRingBaseGeneric, sage.rings.padics.generic_nodes.pAdicFixedModRingGeneric

An implementation of the -adic integers using fixed modulus.

fraction_field(print_mode=None)

Would normally return 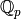, but there is no implementation of 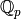matching this ring so this raises an error

If you want to be able to divide with elements of a fixed modulus -adic ring, you must cast explicitly.

EXAMPLES:

sage: ZpFM(5).fraction_field()
...
TypeError: This implementation of the p-adic ring does not support fields of fractions.

sage: a = ZpFM(5)(4); b = ZpFM(5)(5)