Local Generic Element.

This file contains a common superclass for -adic elements and power series elements.

AUTHORS:

• David Roe

class sage.rings.padics.local_generic_element.LocalGenericElement

Bases: sage.structure.element.CommutativeRingElement

is_integral()

Returns whether self is an integral element.

INPUT:

• self – a local ring element

OUTPUT:

• boolean – whether self is an integral element.

EXAMPLES:

sage: R = Qp(3,20)
sage: a = R(7/3); a.is_integral()
False
sage: b = R(7/5); b.is_integral()
True

is_unit()

Returns whether self is a unit

INPUT:

• self – a local ring element

OUTPUT:

• boolean – whether self is a unit

EXAMPLES:

sage: R = Zp(3,20,'capped-rel'); K = Qp(3,20,'capped-rel')
sage: R(0).is_unit()
False
sage: R(1).is_unit()
True
sage: R(2).is_unit()
True
sage: R(3).is_unit()
False

TESTS:

sage: R(4).is_unit()
True
sage: R(6).is_unit()
False
sage: R(9).is_unit()
False
sage: K(0).is_unit()
False
sage: K(1).is_unit()
True
sage: K(2).is_unit()
True
sage: K(3).is_unit()
False
sage: K(4).is_unit()
True
sage: K(6).is_unit()
False
sage: K(9).is_unit()
False
sage: K(1/3).is_unit()
False
sage: K(1/9).is_unit()
False        

normalized_valuation()

Returns the normalized valuation of this local ring element, i.e., the valuation divided by the absolute ramification index.

INPUT:

self – a local ring element.

OUTPUT:

rational – the normalized valuation of self.

EXAMPLES:

sage: Q7 = Qp(7)
sage: R.<x> = Q7[]
sage: F.<z> = Q7.ext(x^3+7*x+7)
sage: z.normalized_valuation()
1/3

slice(i, j, k=1)

Returns the sum of the 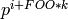terms of the series expansion of self, for 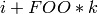between and 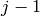inclusive, and 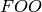an arbitrary integer. Behaves analogously to the slice function for lists.

INPUT:

• self – a -adic element
• i – an integer
• j – an integer
• k – a positive integer, default value 1

EXAMPLES:

sage: R = Zp(5, 6, ‘capped-rel’) sage: a = R(1/2); a 3 + 2*5 + 2*5^2 + 2*5^3 + 2*5^4 + 2*5^5 + O(5^6) sage: a.slice(2, 4) 2*5^2 + 2*5^3 + O(5^4) sage: a.slice(1, 6, 2) 2*5 + 2*5^3 + 2*5^5 + O(5^6) sage: a.slice(5, 4) O(5^4)

sqrt(extend=True, all=False)

TODO: document what “extend” and “all” do

INPUT:

• self – a local ring element

OUTPUT:

• local ring element – the square root of self

EXAMPLES:

sage: R = Zp(13, 10, 'capped-rel', 'series') 
sage: a = sqrt(R(-1)); a * a
12 + 12*13 + 12*13^2 + 12*13^3 + 12*13^4 + 12*13^5 + 12*13^6 + 12*13^7 + 12*13^8 + 12*13^9 + O(13^10)
sage: sqrt(R(4))
2 + O(13^10)
sage: sqrt(R(4/9)) * 3
2 + O(13^10)