This file contains the constructor classes and functions for  -adic rings and fields.
-adic rings and fields.
AUTHORS:
A shortcut function to create capped relative  -adic fields.
-adic fields.
Same functionality as Qp. See documentation for Qp for a description of the input parameters.
EXAMPLES:
sage: QpCR(5, 40)
5-adic Field with capped relative precision 40
Bases: sage.structure.factory.UniqueFactory
A creation function for  -adic fields.
-adic fields.
INPUT:
 in
in 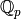
 ). What to use whenever
). What to use whenever  is printed.
is printed. is prime.
Non-prime input may cause seg-faults (but can also be useful for
base n expansions for example)
is prime.
Non-prime input may cause seg-faults (but can also be useful for
base n expansions for example)OUTPUT:
 -adic field.
-adic field.TYPES AND PRECISION:
There are two types of precision for a  -adic element. The first
is relative precision, which gives the number of known
-adic element. The first
is relative precision, which gives the number of known  -adic
digits:
-adic
digits:
sage: R = Qp(5, 20, 'capped-rel', 'series'); a = R(675); a
2*5^2 + 5^4 + O(5^22)
sage: a.precision_relative()
20
The second type of precision is absolute precision, which gives
the power of  that this element is defined modulo:
that this element is defined modulo:
sage: a.precision_absolute()
22
There are two types of  -adic fields: capped relative fields and
lazy fields.
-adic fields: capped relative fields and
lazy fields.
In the capped relative case, the relative precision of an element is restricted to be at most a certain value, specified at the creation of the field. Individual elements also store their own precision, so the effect of various arithmetic operations on precision is tracked. When you cast an exact element into a capped relative field, it truncates it to the precision cap of the field.:
sage: R = Qp(5, 5, 'capped-rel', 'series'); a = R(4006); a
1 + 5 + 2*5^3 + 5^4 + O(5^5)
sage: b = R(4025); b
5^2 + 2*5^3 + 5^4 + 5^5 + O(5^7)
sage: a + b
1 + 5 + 5^2 + 4*5^3 + 2*5^4 + O(5^5)
The lazy case will eventually support elements that can increase their precision upon request. It is not currently implemented.
PRINTING:
There are many different ways to print  -adic elements. The way
elements of a given field print is controlled by options passed in
at the creation of the field. There are five basic printing modes
(series, val-unit, terse, digits and bars), as well as various
options that either hide some information in the print
representation or sometimes make print representations more
compact. Note that the printing options affect whether different
-adic elements. The way
elements of a given field print is controlled by options passed in
at the creation of the field. There are five basic printing modes
(series, val-unit, terse, digits and bars), as well as various
options that either hide some information in the print
representation or sometimes make print representations more
compact. Note that the printing options affect whether different
 -adic fields are considered equal.
-adic fields are considered equal.
series: elements are displayed as series in  .:
.:
sage: R = Qp(5, print_mode='series'); a = R(70700); a
3*5^2 + 3*5^4 + 2*5^5 + 4*5^6 + O(5^22)
sage: b = R(-70700); b
2*5^2 + 4*5^3 + 5^4 + 2*5^5 + 4*5^7 + 4*5^8 + 4*5^9 + 4*5^10 + 4*5^11 + 4*5^12 + 4*5^13 + 4*5^14 + 4*5^15 + 4*5^16 + 4*5^17 + 4*5^18 + 4*5^19 + 4*5^20 + 4*5^21 + O(5^22)
print_pos controls whether negatives can be used in the
coefficients of powers of  .:
.:
sage: S = Qp(5, print_mode='series', print_pos=False); a = S(70700); a
-2*5^2 + 5^3 - 2*5^4 - 2*5^5 + 5^7 + O(5^22)
sage: b = S(-70700); b
2*5^2 - 5^3 + 2*5^4 + 2*5^5 - 5^7 + O(5^22)
print_max_terms limits the number of terms that appear.:
sage: T = Qp(5, print_mode='series', print_max_terms=4); b = R(-70700); repr(b)
'2*5^2 + 4*5^3 + 5^4 + 2*5^5 + ... + O(5^22)'
names affects how the prime is printed.:
sage: U.<p> = Qp(5); p
p + O(p^21)
print_sep and print_alphabet have no effect in series mode.
Note that print options affect equality:
sage: R == S, R == T, R == U, S == T, S == U, T == U
(False, False, False, False, False, False)
val-unit: elements are displayed as p^k*u:
sage: R = Qp(5, print_mode='val-unit'); a = R(70700); a
5^2 * 2828 + O(5^22)
sage: b = R(-707/5); b
5^-1 * 95367431639918 + O(5^19)
print_pos controls whether to use a balanced representation or not.:
sage: S = Qp(5, print_mode='val-unit', print_pos=False); b = S(-70700); b
5^2 * (-2828) + O(5^22)
names affects how the prime is printed.:
sage: T = Qp(5, print_mode='val-unit', names='pi'); a = T(70700); a
pi^2 * 2828 + O(pi^22)
print_max_terms, print_sep and print_alphabet have no effect.
Equality again depends on the printing options:
sage: R == S, R == T, S == T
(False, False, False)
terse: elements are displayed as an integer in base 10 or the
quotient of an integer by a power of  (still in base 10):
(still in base 10):
sage: R = Qp(5, print_mode='terse'); a = R(70700); a
70700 + O(5^22)
sage: b = R(-70700); b
2384185790944925 + O(5^22)
sage: c = R(-707/5); c
95367431639918/5 + O(5^19)
The denominator, as of version 3.3, is always printed
explicitly as a power of  , for predictability.:
, for predictability.:
sage: d = R(707/5^2); d
707/5^2 + O(5^18)
print_pos controls whether to use a balanced representation or not.:
sage: S = Qp(5, print_mode='terse', print_pos=False); b = S(-70700); b
-70700 + O(5^22)
sage: c = S(-707/5); c
-707/5 + O(5^19)
name affects how the name is printed.:
sage: T.<unif> = Qp(5, print_mode='terse'); c = T(-707/5); c
95367431639918/unif + O(unif^19)
sage: d = T(-707/5^10); d
95367431639918/unif^10 + O(unif^10)
print_max_terms, print_sep and print_alphabet have no effect.
Equality depends on printing options:
sage: R == S, R == T, S == T
(False, False, False)
 digits
digitsRestriction: you can only use the digits printing mode for
small primes. Namely,  must be less than the length of the
alphabet tuple (default alphabet has length 62).:
must be less than the length of the
alphabet tuple (default alphabet has length 62).:
sage: R = Qp(5, print_mode='digits'); a = R(70700); repr(a)
'...4230300'
sage: b = R(-70700); repr(b)
'...4444444444444440214200'
sage: c = R(-707/5); repr(c)
'...4444444444444443413.3'
sage: d = R(-707/5^2); repr(d)
'...444444444444444341.33'
Note that it’s not possible to read off the precision from the representation in this mode.
print_max_terms limits the number of digits that are printed. Note that if the valuation of the element is very negative, more digits will be printed.:
sage: S = Qp(5, print_mode='digits', print_max_terms=4); b = S(-70700); repr(b)
'...214200'
sage: d = S(-707/5^2); repr(d)
'...41.33'
sage: e = S(-707/5^6); repr(e)
'...?.434133'
sage: f = S(-707/5^6,absprec=-2); repr(f)
'...?.??4133'
sage: g = S(-707/5^4); repr(g)
'...?.4133'
print_alphabet controls the symbols used to substitute for digits greater than 9.
Defaults to (‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’, ‘A’, ‘B’, ‘C’, ‘D’, ‘E’, ‘F’, ‘G’, ‘H’, ‘I’, ‘J’, ‘K’, ‘L’, ‘M’, ‘N’, ‘O’, ‘P’, ‘Q’, ‘R’, ‘S’, ‘T’, ‘U’, ‘V’, ‘W’, ‘X’, ‘Y’, ‘Z’, ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’, ‘h’, ‘i’, ‘j’, ‘k’, ‘l’, ‘m’, ‘n’, ‘o’, ‘p’, ‘q’, ‘r’, ‘s’, ‘t’, ‘u’, ‘v’, ‘w’, ‘x’, ‘y’, ‘z’):
sage: T = Qp(5, print_mode='digits', print_max_terms=4, print_alphabet=('1','2','3','4','5')); b = T(-70700); repr(b)
'...325311'
print_pos, name and print_sep have no effect.
Equality depends on printing options:
sage: R == S, R == T, S == T
(False, False, False)
bars: elements are displayed as a string of base  digits
with separators:
digits
with separators:
sage: R = Qp(5, print_mode='bars'); a = R(70700); repr(a)
'...4|2|3|0|3|0|0'
sage: b = R(-70700); repr(b)
'...4|4|4|4|4|4|4|4|4|4|4|4|4|4|4|0|2|1|4|2|0|0'
sage: d = R(-707/5^2); repr(d)
'...4|4|4|4|4|4|4|4|4|4|4|4|4|4|4|3|4|1|.|3|3'
Again, note that it’s not possible to read of the precision from the representation in this mode.
print_pos controls whether the digits can be negative.:
sage: S = Qp(5, print_mode='bars',print_pos=False); b = S(-70700); repr(b)
'...-1|0|2|2|-1|2|0|0'
print_max_terms limits the number of digits that are printed. Note that if the valuation of the element is very negative, more digits will be printed.:
sage: T = Qp(5, print_mode='bars', print_max_terms=4); b = T(-70700); repr(b)
'...2|1|4|2|0|0'
sage: d = T(-707/5^2); repr(d)
'...4|1|.|3|3'
sage: e = T(-707/5^6); repr(e)
'...|.|4|3|4|1|3|3'
sage: f = T(-707/5^6,absprec=-2); repr(f)
'...|.|?|?|4|1|3|3'
sage: g = T(-707/5^4); repr(g)
'...|.|4|1|3|3'
print_sep controls the separation character.:
sage: U = Qp(5, print_mode='bars', print_sep=']['); a = U(70700); repr(a)
'...4][2][3][0][3][0][0'
name and print_alphabet have no effect.
Equality depends on printing options:
sage: R == S, R == T, R == U, S == T, S == U, T == U
(False, False, False, False, False, False)
EXAMPLES:
sage: K = Qp(15, check=False); a = K(999); a
9 + 6*15 + 4*15^2 + O(15^20)
Creates a key from input parameters for Qp.
See the documentation for Qp for more information.
TESTS:
sage: Qp.create_key(5,40)
(5, 40, 'capped-rel', 'series', '5', True, '|', ('0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z'), -1)
Creates an object using a given key.
See the documentation for Qp for more information.
TESTS:
sage: Qp.create_object((3,4,2),(5, 40, 'capped-rel', 'series', '5', True, '|', ('0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z'), -1))
5-adic Field with capped relative precision 40
Given a prime power 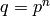 , return the unique unramified
extension of
, return the unique unramified
extension of 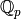 of degree
of degree  .
.
INPUT:
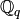 . OR, if check=False, a
factorization object or single element list [(p, n)] where p is
a prime and n a positive integer.
. OR, if check=False, a
factorization object or single element list [(p, n)] where p is
a prime and n a positive integer.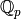 . See MODULUS below.
. See MODULUS below.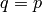 ). The
name of the generator, reducing to a generator of the residue
field.
). The
name of the generator, reducing to a generator of the residue
field. if
None). ram_name controls how the prime is printed. See PRINTING
below.
if
None). ram_name controls how the prime is printed. See PRINTING
below. shown. See PRINTING below.
shown. See PRINTING below. . See PRINTING
below.
. See PRINTING
below.OUTPUT:
 -adic field.
-adic field.TYPES AND PRECISION:
There are two types of precision for a  -adic element. The first
is relative precision, which gives the number of known
-adic element. The first
is relative precision, which gives the number of known  -adic
digits:
-adic
digits:
sage: R.<a> = Qq(25, 20, 'capped-rel', print_mode='series'); b = 25*a; b
a*5^2 + O(5^22)
sage: b.precision_relative()
20
The second type of precision is absolute precision, which gives
the power of  that this element is defined modulo:
that this element is defined modulo:
sage: b.precision_absolute()
22
There are two types of unramified  -adic fields: capped relative
fields and lazy fields.
-adic fields: capped relative
fields and lazy fields.
In the capped relative case, the relative precision of an element is restricted to be at most a certain value, specified at the creation of the field. Individual elements also store their own precision, so the effect of various arithmetic operations on precision is tracked. When you cast an exact element into a capped relative field, it truncates it to the precision cap of the field.:
sage: R.<a> = Qq(9, 5, 'capped-rel', print_mode='series'); b = (1+2*a)^4; b
2 + (2*a + 2)*3 + (2*a + 1)*3^2 + O(3^5)
sage: c = R(3249); c
3^2 + 3^4 + 3^5 + 3^6 + O(3^7)
sage: b + c
2 + (2*a + 2)*3 + (2*a + 2)*3^2 + 3^4 + O(3^5)
The lazy case will eventually support elements that can increase their precision upon request. It is not currently implemented.
MODULUS:
The modulus needs to define an unramified extension of 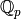 : when it
is reduced to a polynomial over
: when it
is reduced to a polynomial over 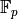 it should be irreducible.
it should be irreducible.
The modulus can be given in a number of forms.
The base ring can be 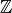 ,
, 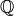 ,
,  ,
, 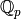 ,
, 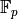 .:
.:
sage: P.<x> = ZZ[]
sage: R.<a> = Qq(27, modulus = x^3 + 2*x + 1); R.modulus()
(1 + O(3^20))*x^3 + (O(3^20))*x^2 + (2 + O(3^20))*x + (1 + O(3^20))
sage: P.<x> = QQ[]
sage: S.<a> = Qq(27, modulus = x^3 + 2*x + 1)
sage: P.<x> = Zp(3)[]
sage: T.<a> = Qq(27, modulus = x^3 + 2*x + 1)
sage: P.<x> = Qp(3)[]
sage: U.<a> = Qq(27, modulus = x^3 + 2*x + 1)
sage: P.<x> = GF(3)[]
sage: V.<a> = Qq(27, modulus = x^3 + 2*x + 1)
Which form the modulus is given in has no effect on the unramified extension produced:
sage: R == S, S == T, T == U, U == V
(True, True, True, False)
unless the precision of the modulus differs. In the case of V, the modulus is only given to precision 1, so the resulting field has a precision cap of 1.:
sage: V.precision_cap()
1
sage: U.precision_cap()
20
sage: P.<x> = Qp(3)[]
sage: modulus = x^3 + (2 + O(3^7))*x + (1 + O(3^10))
sage: modulus
(1 + O(3^20))*x^3 + (2 + O(3^7))*x + (1 + O(3^10))
sage: W.<a> = Qq(27, modulus = modulus); W.precision_cap()
7
The modulus can also be given as a symbolic expression.:
sage: x = var('x')
sage: X.<a> = Qq(27, modulus = x^3 + 2*x + 1); X.modulus()
(1 + O(3^20))*x^3 + (O(3^20))*x^2 + (2 + O(3^20))*x + (1 + O(3^20))
sage: X == R
True
By default, the polynomial chosen is the standard lift of the
generator chosen for 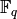 .:
.:
sage: GF(125, 'a').modulus()
x^3 + 3*x + 3
sage: Y.<a> = Qq(125); Y.modulus()
(1 + O(5^20))*x^3 + (O(5^20))*x^2 + (3 + O(5^20))*x + (3 + O(5^20))
However, you can choose another polynomial if desired (as long as
the reduction to ![\mathbb{F}_p[x]](../../../_images/math/e5a21492095c9116b100e2f7626a70cc26834e82.png) is irreducible).:
is irreducible).:
sage: P.<x> = ZZ[]
sage: Z.<a> = Qq(125, modulus = x^3 + 3*x^2 + x + 1); Z.modulus()
(1 + O(5^20))*x^3 + (3 + O(5^20))*x^2 + (1 + O(5^20))*x + (1 + O(5^20))
sage: Y == Z
False
PRINTING:
There are many different ways to print  -adic elements. The way
elements of a given field print is controlled by options passed in
at the creation of the field. There are four basic printing modes
('series', 'val-unit', 'terse' and 'bars'; 'digits' is not available), as
well as various options that either hide some information in the
print representation or sometimes make print representations more
compact. Note that the printing options affect whether different
-adic elements. The way
elements of a given field print is controlled by options passed in
at the creation of the field. There are four basic printing modes
('series', 'val-unit', 'terse' and 'bars'; 'digits' is not available), as
well as various options that either hide some information in the
print representation or sometimes make print representations more
compact. Note that the printing options affect whether different
 -adic fields are considered equal.
-adic fields are considered equal.
series: elements are displayed as series in  .:
.:
sage: R.<a> = Qq(9, 20, 'capped-rel', print_mode='series'); (1+2*a)^4
2 + (2*a + 2)*3 + (2*a + 1)*3^2 + O(3^20)
sage: -3*(1+2*a)^4
3 + a*3^2 + 3^3 + (2*a + 2)*3^4 + (2*a + 2)*3^5 + (2*a + 2)*3^6 + (2*a + 2)*3^7 + (2*a + 2)*3^8 + (2*a + 2)*3^9 + (2*a + 2)*3^10 + (2*a + 2)*3^11 + (2*a + 2)*3^12 + (2*a + 2)*3^13 + (2*a + 2)*3^14 + (2*a + 2)*3^15 + (2*a + 2)*3^16 + (2*a + 2)*3^17 + (2*a + 2)*3^18 + (2*a + 2)*3^19 + (2*a + 2)*3^20 + O(3^21)
sage: ~(3*a+18)
(a + 2)*3^-1 + 1 + 2*3 + (a + 1)*3^2 + 3^3 + 2*3^4 + (a + 1)*3^5 + 3^6 + 2*3^7 + (a + 1)*3^8 + 3^9 + 2*3^10 + (a + 1)*3^11 + 3^12 + 2*3^13 + (a + 1)*3^14 + 3^15 + 2*3^16 + (a + 1)*3^17 + 3^18 + O(3^19)
print_pos controls whether negatives can be used in the
coefficients of powers of  .:
.:
sage: S.<b> = Qq(9, print_mode='series', print_pos=False); (1+2*b)^4
-1 - b*3 - 3^2 + (b + 1)*3^3 + O(3^20)
sage: -3*(1+2*b)^4
3 + b*3^2 + 3^3 + (-b - 1)*3^4 + O(3^21)
ram_name controls how the prime is printed.:
sage: T.<d> = Qq(9, print_mode='series', ram_name='p'); 3*(1+2*d)^4
2*p + (2*d + 2)*p^2 + (2*d + 1)*p^3 + O(p^21)
print_max_ram_terms limits the number of powers of  that appear.:
that appear.:
sage: U.<e> = Qq(9, print_mode='series', print_max_ram_terms=4); repr(-3*(1+2*e)^4)
'3 + e*3^2 + 3^3 + (2*e + 2)*3^4 + ... + O(3^21)'
print_max_unram_terms limits the number of terms that appear in a
coefficient of a power of  .:
.:
sage: V.<f> = Qq(128, prec = 8, print_mode='series'); repr((1+f)^9)
'(f^3 + 1) + (f^5 + f^4 + f^3 + f^2)*2 + (f^6 + f^5 + f^4 + f + 1)*2^2 + (f^5 + f^4 + f^2 + f + 1)*2^3 + (f^6 + f^5 + f^4 + f^3 + f^2 + f + 1)*2^4 + (f^5 + f^4)*2^5 + (f^6 + f^5 + f^4 + f^3 + f + 1)*2^6 + (f + 1)*2^7 + O(2^8)'
sage: V.<f> = Qq(128, prec = 8, print_mode='series', print_max_unram_terms = 3); repr((1+f)^9)
'(f^3 + 1) + (f^5 + f^4 + ... + f^2)*2 + (f^6 + f^5 + ... + 1)*2^2 + (f^5 + f^4 + ... + 1)*2^3 + (f^6 + f^5 + ... + 1)*2^4 + (f^5 + f^4)*2^5 + (f^6 + f^5 + ... + 1)*2^6 + (f + 1)*2^7 + O(2^8)'
sage: V.<f> = Qq(128, prec = 8, print_mode='series', print_max_unram_terms = 2); repr((1+f)^9)
'(f^3 + 1) + (f^5 + ... + f^2)*2 + (f^6 + ... + 1)*2^2 + (f^5 + ... + 1)*2^3 + (f^6 + ... + 1)*2^4 + (f^5 + f^4)*2^5 + (f^6 + ... + 1)*2^6 + (f + 1)*2^7 + O(2^8)'
sage: V.<f> = Qq(128, prec = 8, print_mode='series', print_max_unram_terms = 1); repr((1+f)^9)
'(f^3 + ...) + (f^5 + ...)*2 + (f^6 + ...)*2^2 + (f^5 + ...)*2^3 + (f^6 + ...)*2^4 + (f^5 + ...)*2^5 + (f^6 + ...)*2^6 + (f + ...)*2^7 + O(2^8)'
sage: V.<f> = Qq(128, prec = 8, print_mode='series', print_max_unram_terms = 0); repr((1+f)^9 - 1 - f^3)
'(...)*2 + (...)*2^2 + (...)*2^3 + (...)*2^4 + (...)*2^5 + (...)*2^6 + (...)*2^7 + O(2^8)'
print_sep and print_max_terse_terms have no effect.
Note that print options affect equality:
sage: R == S, R == T, R == U, R == V, S == T, S == U, S == V, T == U, T == V, U == V
(False, False, False, False, False, False, False, False, False, False)
val-unit: elements are displayed as 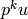 :
:
sage: R.<a> = Qq(9, 7, print_mode='val-unit'); b = (1+3*a)^9 - 1; b
3^3 * (15 + 64*a) + O(3^7)
sage: ~b
3^-3 * (41 + a) + O(3)
print_pos controls whether to use a balanced representation or not.:
sage: S.<a> = Qq(9, 7, print_mode='val-unit', print_pos=False); b = (1+3*a)^9 - 1; b
3^3 * (15 - 17*a) + O(3^7)
sage: ~b
3^-3 * (-40 + a) + O(3)
ram_name affects how the prime is printed.:
sage: A.<x> = Qp(next_prime(10^6), print_mode='val-unit')[]
sage: T.<a> = Qq(next_prime(10^6)^3, 4, print_mode='val-unit', ram_name='p', modulus=x^3+385831*x^2+106556*x+321036); b = ~(next_prime(10^6)^2*(a^2 + a - 4)); b
p^-2 * (503009563508519137754940 + 704413692798200940253892*a + 968097057817740999537581*a^2) + O(p^2)
sage: b * (a^2 + a - 4)
p^-2 * 1 + O(p^2)
print_max_terse_terms controls how many terms of the polynomial appear in the unit part.:
sage: U.<a> = Qq(17^4, 6, print_mode='val-unit', print_max_terse_terms=3); b = ~(17*(a^3-a+14)); b
17^-1 * (22110411 + 11317400*a + 20656972*a^2 + ...) + O(17^5)
sage: b*17*(a^3-a+14)
1 + O(17^6)
print_sep, print_max_ram_terms and print_max_unram_terms have no effect.
Equality again depends on the printing options:
sage: R == S, R == T, R == U, S == T, S == U, T == U
(False, False, False, False, False, False)
terse: elements are displayed as a polynomial of degree less than the degree of the extension.:
sage: R.<a> = Qq(125, print_mode='terse')
sage: (a+5)^177
68210977979428 + 90313850704069*a + 73948093055069*a^2 + O(5^20)
sage: (a/5+1)^177
68210977979428/5^177 + 90313850704069/5^177*a + 73948093055069/5^177*a^2 + O(5^-157)
As of version 3.3, if coefficients of the polynomial are
non-integral, they are always printed with an explicit power of  in the denominator.:
in the denominator.:
sage: 5*a + a^2/25
5*a + 1/5^2*a^2 + O(5^18)
print_pos controls whether to use a balanced representation or not.:
sage: (a-5)^6
22864 + 95367431627998*a + 8349*a^2 + O(5^20)
sage: S.<a> = Qq(125, print_mode='terse', print_pos=False); b = (a-5)^6; b
22864 - 12627*a + 8349*a^2 + O(5^20)
sage: (a - 1/5)^6
-20624/5^6 + 18369/5^5*a + 1353/5^3*a^2 + O(5^14)
ram_name affects how the prime is printed.:
sage: T.<a> = Qq(125, print_mode='terse', ram_name='p'); (a - 1/5)^6
95367431620001/p^6 + 18369/p^5*a + 1353/p^3*a^2 + O(p^14)
print_max_terse_terms controls how many terms of the polynomial are shown.:
sage: U.<a> = Qq(625, print_mode='terse', print_max_terse_terms=2); (a-1/5)^6
106251/5^6 + 49994/5^5*a + ... + O(5^14)
print_sep, print_max_ram_terms and print_max_unram_terms have no effect.
Equality again depends on the printing options:
sage: R == S, R == T, R == U, S == T, S == U, T == U
(False, False, False, False, False, False)
It might make sense to have a dictionary for small fields, but this isn’t implemented.
bars: elements are displayed in a similar fashion to series, but more compactly.:
sage: R.<a> = Qq(125); (a+5)^6
(4*a^2 + 3*a + 4) + (3*a^2 + 2*a)*5 + (a^2 + a + 1)*5^2 + (3*a + 2)*5^3 + (3*a^2 + a + 3)*5^4 + (2*a^2 + 3*a + 2)*5^5 + O(5^20)
sage: R.<a> = Qq(125, print_mode='bars', prec=8); repr((a+5)^6)
'...[2, 3, 2]|[3, 1, 3]|[2, 3]|[1, 1, 1]|[0, 2, 3]|[4, 3, 4]'
sage: repr((a-5)^6)
'...[0, 4]|[1, 4]|[2, 0, 2]|[1, 4, 3]|[2, 3, 1]|[4, 4, 3]|[2, 4, 4]|[4, 3, 4]'
Note that elements with negative valuation are shown with a decimal point at valuation 0.:
sage: repr((a+1/5)^6)
'...[3]|[4, 1, 3]|.|[1, 2, 3]|[3, 3]|[0, 0, 3]|[0, 1]|[0, 1]|[1]'
sage: repr((a+1/5)^2)
'...[0, 0, 1]|.|[0, 2]|[1]'
If not enough precision is known, '?' is used instead.:
sage: repr((a+R(1/5,relprec=3))^7)
'...|.|?|?|?|?|[0, 1, 1]|[0, 2]|[1]'
Note that it’s not possible to read of the precision from the representation in this mode.:
sage: b = a + 3; repr(b)
'...[3, 1]'
sage: c = a + R(3, 4); repr(c)
'...[3, 1]'
sage: b.precision_absolute()
8
sage: c.precision_absolute()
4
print_pos controls whether the digits can be negative.:
sage: S.<a> = Qq(125, print_mode='bars', print_pos=False); repr((a-5)^6)
'...[1, -1, 1]|[2, 1, -2]|[2, 0, -2]|[-2, -1, 2]|[0, 0, -1]|[-2]|[-1, -2, -1]'
sage: repr((a-1/5)^6)
'...[0, 1, 2]|[-1, 1, 1]|.|[-2, -1, -1]|[2, 2, 1]|[0, 0, -2]|[0, -1]|[0, -1]|[1]'
print_max_ram_terms controls the maximum number of “digits” shown. Note that this puts a cap on the relative precision, not the absolute precision.:
sage: T.<a> = Qq(125, print_mode='bars', print_max_ram_terms=3, print_pos=False); repr((a-5)^6)
'...[0, 0, -1]|[-2]|[-1, -2, -1]'
sage: repr(5*(a-5)^6+50)
'...[0, 0, -1]|[]|[-1, -2, -1]|[]'
However, if the element has negative valuation, digits are shown up to the decimal point.:
sage: repr((a-1/5)^6)
'...|.|[-2, -1, -1]|[2, 2, 1]|[0, 0, -2]|[0, -1]|[0, -1]|[1]'
print_sep controls the separating character ('|' by default).:
sage: U.<a> = Qq(625, print_mode='bars', print_sep=''); b = (a+5)^6; repr(b)
'...[0, 1][4, 0, 2][3, 2, 2, 3][4, 2, 2, 4][0, 3][1, 1, 3][3, 1, 4, 1]'
print_max_unram_terms controls how many terms are shown in each “digit”:
sage: with local_print_mode(U, {'max_unram_terms': 3}): repr(b)
'...[0, 1][4,..., 0, 2][3,..., 2, 3][4,..., 2, 4][0, 3][1,..., 1, 3][3,..., 4, 1]'
sage: with local_print_mode(U, {'max_unram_terms': 2}): repr(b)
'...[0, 1][4,..., 2][3,..., 3][4,..., 4][0, 3][1,..., 3][3,..., 1]'
sage: with local_print_mode(U, {'max_unram_terms': 1}): repr(b)
'...[..., 1][..., 2][..., 3][..., 4][..., 3][..., 3][..., 1]'
sage: with local_print_mode(U, {'max_unram_terms':0}): repr(b-75*a)
'...[...][...][...][...][][...][...]'
ram_name and print_max_terse_terms have no effect.
Equality depends on printing options:
sage: R == S, R == T, R == U, S == T, S == U, T == U
(False, False, False, False, False, False)
EXAMPLES
Unlike for Qp, you can’t create Qq(N) when N is not a prime power.
However, you can use check=False to pass in a pair in order to not have to factor. If you do so, you need to use names explicitly rather than the R.<a> syntax.:
sage: p = next_prime(2^123)
sage: k = Qp(p)
sage: R.<x> = k[]
sage: K = Qq([(p, 5)], modulus=x^5+x+4, names='a', ram_name='p', print_pos=False, check=False)
sage: K.0^5
(-a - 4) + O(p^20)
In tests on sage.math.washington.edu, the creation of K as above took an average of 1.58ms, while:
sage: K = Qq(p^5, modulus=x^5+x+4, names='a', ram_name='p', print_pos=False, check=True)
took an average of 24.5ms. Of course, with smaller primes these savings disappear.
A shortcut function to create capped relative unramified  -adic
fields.
-adic
fields.
Same functionality as Qq. See documentation for Qq for a description of the input parameters.
EXAMPLES:
sage: R.<a> = QqCR(25, 40); R
Unramified Extension of 5-adic Field with capped relative precision 40 in a defined by (1 + O(5^40))*x^2 + (4 + O(5^40))*x + (2 + O(5^40))
A shortcut function to create capped absolute  -adic rings.
-adic rings.
See documentation for Zp for a description of the input parameters.
EXAMPLES:
sage: ZpCA(5, 40)
5-adic Ring with capped absolute precision 40
A shortcut function to create capped relative  -adic rings.
-adic rings.
Same functionality as Zp. See documentation for Zp for a description of the input parameters.
EXAMPLES:
sage: ZpCR(5, 40)
5-adic Ring with capped relative precision 40
A shortcut function to create fixed modulus  -adic rings.
-adic rings.
See documentation for Zp for a description of the input parameters.
EXAMPLES:
sage: ZpFM(5, 40)
5-adic Ring of fixed modulus 5^40
Bases: sage.structure.factory.UniqueFactory
A creation function for  -adic rings.
-adic rings.
INPUT:
 in
in 
 ). What to use whenever
). What to use whenever  is printed.
is printed. is
prime. Non-prime input may cause seg-faults (but can also be
useful for base
is
prime. Non-prime input may cause seg-faults (but can also be
useful for base  expansions for example)
expansions for example)OUTPUT:
 -adic ring.
-adic ring.TYPES AND PRECISION:
There are two types of precision for a  -adic element. The first
is relative precision, which gives the number of known
-adic element. The first
is relative precision, which gives the number of known  -adic
digits:
-adic
digits:
sage: R = Zp(5, 20, 'capped-rel', 'series'); a = R(675); a
2*5^2 + 5^4 + O(5^22)
sage: a.precision_relative()
20
The second type of precision is absolute precision, which gives
the power of  that this element is defined modulo:
that this element is defined modulo:
sage: a.precision_absolute()
22
There are four types of  -adic rings: capped relative rings
(type= 'capped-rel'), capped absolute rings
(type= 'capped-abs'), fixed modulus ring (type= 'fixed-mod')
and lazy rings (type= 'lazy').
-adic rings: capped relative rings
(type= 'capped-rel'), capped absolute rings
(type= 'capped-abs'), fixed modulus ring (type= 'fixed-mod')
and lazy rings (type= 'lazy').
In the capped relative case, the relative precision of an element is restricted to be at most a certain value, specified at the creation of the field. Individual elements also store their own precision, so the effect of various arithmetic operations on precision is tracked. When you cast an exact element into a capped relative field, it truncates it to the precision cap of the field.:
sage: R = Zp(5, 5, 'capped-rel', 'series'); a = R(4006); a
1 + 5 + 2*5^3 + 5^4 + O(5^5)
sage: b = R(4025); b
5^2 + 2*5^3 + 5^4 + 5^5 + O(5^7)
sage: a + b
1 + 5 + 5^2 + 4*5^3 + 2*5^4 + O(5^5)
In the capped absolute type, instead of having a cap on the relative precision of an element there is instead a cap on the absolute precision. Elements still store their own precisions, and as with the capped relative case, exact elements are truncated when cast into the ring.:
sage: R = Zp(5, 5, 'capped-abs', 'series'); a = R(4005); a
5 + 2*5^3 + 5^4 + O(5^5)
sage: b = R(4025); b
5^2 + 2*5^3 + 5^4 + O(5^5)
sage: a * b
5^3 + 2*5^4 + O(5^5)
sage: (a * b) // 5^3
1 + 2*5 + O(5^2)
The fixed modulus type is the leanest of the  -adic rings: it is
basically just a wrapper around
-adic rings: it is
basically just a wrapper around 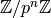 providing a unified
interface with the rest of the
providing a unified
interface with the rest of the  -adics. This is the type you
should use if your sole interest is speed. It does not track
precision of elements.:
-adics. This is the type you
should use if your sole interest is speed. It does not track
precision of elements.:
sage: R = Zp(5,5,'fixed-mod','series'); a = R(4005); a
5 + 2*5^3 + 5^4 + O(5^5)
sage: a // 5
1 + 2*5^2 + 5^3 + O(5^5)
The lazy case will eventually support elements that can increase their precision upon request. It is not currently implemented.
PRINTING
There are many different ways to print  -adic elements. The
way elements of a given ring print is controlled by options
passed in at the creation of the ring. There are five basic
printing modes (series, val-unit, terse, digits and bars), as
well as various options that either hide some information in
the print representation or sometimes make print
representations more compact. Note that the printing options
affect whether different
-adic elements. The
way elements of a given ring print is controlled by options
passed in at the creation of the ring. There are five basic
printing modes (series, val-unit, terse, digits and bars), as
well as various options that either hide some information in
the print representation or sometimes make print
representations more compact. Note that the printing options
affect whether different  -adic fields are considered equal.
-adic fields are considered equal.
series: elements are displayed as series in  .:
.:
sage: R = Zp(5, print_mode='series'); a = R(70700); a
3*5^2 + 3*5^4 + 2*5^5 + 4*5^6 + O(5^22)
sage: b = R(-70700); b
2*5^2 + 4*5^3 + 5^4 + 2*5^5 + 4*5^7 + 4*5^8 + 4*5^9 + 4*5^10 + 4*5^11 + 4*5^12 + 4*5^13 + 4*5^14 + 4*5^15 + 4*5^16 + 4*5^17 + 4*5^18 + 4*5^19 + 4*5^20 + 4*5^21 + O(5^22)
print_pos controls whether negatives can be used in the
coefficients of powers of  .:
.:
sage: S = Zp(5, print_mode='series', print_pos=False); a = S(70700); a
-2*5^2 + 5^3 - 2*5^4 - 2*5^5 + 5^7 + O(5^22)
sage: b = S(-70700); b
2*5^2 - 5^3 + 2*5^4 + 2*5^5 - 5^7 + O(5^22)
print_max_terms limits the number of terms that appear.:
sage: T = Zp(5, print_mode='series', print_max_terms=4); b = R(-70700); b
2*5^2 + 4*5^3 + 5^4 + 2*5^5 + ... + O(5^22)
names affects how the prime is printed.:
sage: U.<p> = Zp(5); p
p + O(p^21)
print_sep and print_alphabet have no effect.
Note that print options affect equality:
sage: R == S, R == T, R == U, S == T, S == U, T == U
(False, False, False, False, False, False)
val-unit: elements are displayed as 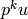 :
:
sage: R = Zp(5, print_mode='val-unit'); a = R(70700); a
5^2 * 2828 + O(5^22)
sage: b = R(-707*5); b
5 * 95367431639918 + O(5^21)
print_pos controls whether to use a balanced representation or not.:
sage: S = Zp(5, print_mode='val-unit', print_pos=False); b = S(-70700); b
5^2 * (-2828) + O(5^22)
names affects how the prime is printed.:
sage: T = Zp(5, print_mode='val-unit', names='pi'); a = T(70700); a
pi^2 * 2828 + O(pi^22)
print_max_terms, print_sep and print_alphabet have no effect.
Equality again depends on the printing options:
sage: R == S, R == T, S == T
(False, False, False)
terse: elements are displayed as an integer in base 10:
sage: R = Zp(5, print_mode='terse'); a = R(70700); a
70700 + O(5^22)
sage: b = R(-70700); b
2384185790944925 + O(5^22)
print_pos controls whether to use a balanced representation or not.:
sage: S = Zp(5, print_mode='terse', print_pos=False); b = S(-70700); b
-70700 + O(5^22)
name affects how the name is printed. Note that this interacts with the choice of shorter string for denominators.:
sage: T.<unif> = Zp(5, print_mode='terse'); c = T(-707); c
95367431639918 + O(unif^20)
print_max_terms, print_sep and print_alphabet have no effect.
Equality depends on printing options:
sage: R == S, R == T, S == T
(False, False, False)
 digits
digitsRestriction: you can only use the digits printing mode for small
primes. Namely,  must be less than the length of the alphabet
tuple (default alphabet has length 62).:
must be less than the length of the alphabet
tuple (default alphabet has length 62).:
sage: R = Zp(5, print_mode='digits'); a = R(70700); repr(a)
'...4230300'
sage: b = R(-70700); repr(b)
'...4444444444444440214200'
Note that it’s not possible to read off the precision from the representation in this mode.
print_max_terms limits the number of digits that are printed.:
sage: S = Zp(5, print_mode='digits', print_max_terms=4); b = S(-70700); repr(b)
'...214200'
print_alphabet controls the symbols used to substitute for digits greater than 9. Defaults to (‘0’, ‘1’, ‘2’, ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, ‘8’, ‘9’, ‘A’, ‘B’, ‘C’, ‘D’, ‘E’, ‘F’, ‘G’, ‘H’, ‘I’, ‘J’, ‘K’, ‘L’, ‘M’, ‘N’, ‘O’, ‘P’, ‘Q’, ‘R’, ‘S’, ‘T’, ‘U’, ‘V’, ‘W’, ‘X’, ‘Y’, ‘Z’, ‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’, ‘g’, ‘h’, ‘i’, ‘j’, ‘k’, ‘l’, ‘m’, ‘n’, ‘o’, ‘p’, ‘q’, ‘r’, ‘s’, ‘t’, ‘u’, ‘v’, ‘w’, ‘x’, ‘y’, ‘z’):
sage: T = Zp(5, print_mode='digits', print_max_terms=4, print_alphabet=('1','2','3','4','5')); b = T(-70700); repr(b)
'...325311'
print_pos, name and print_sep have no effect.
Equality depends on printing options:
sage: R == S, R == T, S == T
(False, False, False)
bars: elements are displayed as a string of base  digits
with separators
digits
with separators
sage: R = Zp(5, print_mode=’bars’); a = R(70700); repr(a) ‘...4|2|3|0|3|0|0’ sage: b = R(-70700); repr(b) ‘...4|4|4|4|4|4|4|4|4|4|4|4|4|4|4|0|2|1|4|2|0|0’
Again, note that it’s not possible to read of the precision from the representation in this mode.
print_pos controls whether the digits can be negative.:
sage: S = Zp(5, print_mode='bars',print_pos=False); b = S(-70700); repr(b)
'...-1|0|2|2|-1|2|0|0'
print_max_terms limits the number of digits that are printed.:
sage: T = Zp(5, print_mode='bars', print_max_terms=4); b = T(-70700); repr(b)
'...2|1|4|2|0|0'
print_sep controls the separation character.:
sage: U = Zp(5, print_mode='bars', print_sep=']['); a = U(70700); repr(a)
'...4][2][3][0][3][0][0'
name and print_alphabet have no effect.
Equality depends on printing options:
sage: R == S, R == T, R == U, S == T, S == U, T == U
(False, False, False, False, False, False)
EXAMPLES:
We allow non-prime  , but only if check = False. Note that some
features will not work.:
, but only if check = False. Note that some
features will not work.:
sage: K = Zp(15, check=False); a = K(999); a
9 + 6*15 + 4*15^2 + O(15^20)
We create rings with various parameters:
sage: Zp(7)
7-adic Ring with capped relative precision 20
sage: Zp(9)
...
ValueError: p must be prime
sage: Zp(17, 5)
17-adic Ring with capped relative precision 5
sage: Zp(17, 5)(-1)
16 + 16*17 + 16*17^2 + 16*17^3 + 16*17^4 + O(17^5)
It works even with a fairly huge cap:
sage: Zp(next_prime(10^50), 100000)
100000000000000000000000000000000000000000000000151-adic Ring with capped relative precision 100000
We create each type of ring:
sage: Zp(7, 20, 'capped-rel')
7-adic Ring with capped relative precision 20
sage: Zp(7, 20, 'fixed-mod')
7-adic Ring of fixed modulus 7^20
sage: Zp(7, 20, 'capped-abs')
7-adic Ring with capped absolute precision 20
We create a capped relative ring with each print mode:
sage: k = Zp(7, 8, print_mode='series'); k
7-adic Ring with capped relative precision 8
sage: k(7*(19))
5*7 + 2*7^2 + O(7^9)
sage: k(7*(-19))
2*7 + 4*7^2 + 6*7^3 + 6*7^4 + 6*7^5 + 6*7^6 + 6*7^7 + 6*7^8 + O(7^9)
sage: k = Zp(7, print_mode='val-unit'); k
7-adic Ring with capped relative precision 20
sage: k(7*(19))
7 * 19 + O(7^21)
sage: k(7*(-19))
7 * 79792266297611982 + O(7^21)
sage: k = Zp(7, print_mode='terse'); k
7-adic Ring with capped relative precision 20
sage: k(7*(19))
133 + O(7^21)
sage: k(7*(-19))
558545864083283874 + O(7^21)
Note that  -adic rings are cached (via weak references):
-adic rings are cached (via weak references):
sage: a = Zp(7); b = Zp(7)
sage: a is b
True
We create some elements in various rings:
sage: R = Zp(5); a = R(4); a
4 + O(5^20)
sage: S = Zp(5, 10, type = 'capped-abs'); b = S(2); b
2 + O(5^10)
sage: a + b
1 + 5 + O(5^10)
Creates a key from input parameters for Zp.
See the documentation for Zp for more information.
TESTS:
sage: Zp.create_key(5,40)
(5, 40, 'capped-rel', 'series', '5', True, '|', ('0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z'), -1)
Creates an object using a given key.
See the documentation for Zp for more information.
TESTS:
sage: Zp.create_object((3,4,2),(5, 40, 'capped-rel', 'series', '5', True, '|', ('0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z'), -1))
5-adic Ring with capped relative precision 40
Given a prime power 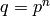 , return the unique unramified
extension of
, return the unique unramified
extension of  of degree
of degree  .
.
INPUT:
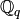 . OR, if
check=False, a factorization object or single element list
[(p, n)] where p is a prime and n a positive
integer.
. OR, if
check=False, a factorization object or single element list
[(p, n)] where p is a prime and n a positive
integer. . See MODULUS below.
. See MODULUS below.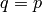 ). The name of the generator, reducing to a generator of
the residue field.
). The name of the generator, reducing to a generator of
the residue field. if
None). ram_name controls how the prime is printed. See PRINTING
below.
if
None). ram_name controls how the prime is printed. See PRINTING
below. shown. See PRINTING below.
shown. See PRINTING below. . See
PRINTING below.
. See
PRINTING below.OUTPUT:
 -adic ring.
-adic ring.TYPES AND PRECISION:
There are two types of precision for a  -adic element. The first
is relative precision, which gives the number of known
-adic element. The first
is relative precision, which gives the number of known  -adic
digits:
-adic
digits:
sage: R.<a> = Zq(25, 20, 'capped-rel', print_mode='series'); b = 25*a; b
a*5^2 + O(5^22)
sage: b.precision_relative()
20
The second type of precision is absolute precision, which gives
the power of  that this element is defined modulo:
that this element is defined modulo:
sage: b.precision_absolute()
22
There are four types of unramified  -adic rings: capped relative
rings, capped absolute rings, fixed modulus rings, and lazy rings.
-adic rings: capped relative
rings, capped absolute rings, fixed modulus rings, and lazy rings.
In the capped relative case, the relative precision of an element is restricted to be at most a certain value, specified at the creation of the field. Individual elements also store their own precision, so the effect of various arithmetic operations on precision is tracked. When you cast an exact element into a capped relative field, it truncates it to the precision cap of the field.:
sage: R.<a> = Zq(9, 5, 'capped-rel', print_mode='series'); b = (1+2*a)^4; b
2 + (2*a + 2)*3 + (2*a + 1)*3^2 + O(3^5)
sage: c = R(3249); c
3^2 + 3^4 + 3^5 + 3^6 + O(3^7)
sage: b + c
2 + (2*a + 2)*3 + (2*a + 2)*3^2 + 3^4 + O(3^5)
One can invert non-units: the result is in the fraction field.:
sage: d = ~(3*b+c); d
2*3^-1 + (a + 1) + (a + 1)*3 + a*3^3 + O(3^4)
sage: d.parent()
Unramified Extension of 3-adic Field with capped relative precision 5 in a defined by (1 + O(3^5))*x^2 + (2 + O(3^5))*x + (2 + O(3^5))
The capped absolute case is the same as the capped relative case, except that the cap is on the absolute precision rather than the relative precision.:
sage: R.<a> = Zq(9, 5, 'capped-abs', print_mode='series'); b = 3*(1+2*a)^4; b
2*3 + (2*a + 2)*3^2 + (2*a + 1)*3^3 + O(3^5)
sage: c = R(3249); c
3^2 + 3^4 + O(3^5)
sage: b*c
2*3^3 + (2*a + 2)*3^4 + O(3^5)
sage: b*c >> 1
2*3^2 + (2*a + 2)*3^3 + O(3^4)
The fixed modulus case is like the capped absolute, except that individual elements don’t track their precision.:
sage: R.<a> = Zq(9, 5, 'fixed-mod', print_mode='series'); b = 3*(1+2*a)^4; b
2*3 + (2*a + 2)*3^2 + (2*a + 1)*3^3 + O(3^5)
sage: c = R(3249); c
3^2 + 3^4 + O(3^5)
sage: b*c
2*3^3 + (2*a + 2)*3^4 + O(3^5)
sage: b*c >> 1
2*3^2 + (2*a + 2)*3^3 + O(3^5)
The lazy case will eventually support elements that can increase their precision upon request. It is not currently implemented.
MODULUS:
The modulus needs to define an unramified extension of  : when it
is reduced to a polynomial over
: when it
is reduced to a polynomial over 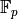 it should be irreducible.
it should be irreducible.
The modulus can be given in a number of forms.
The base ring can be 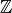 ,
, 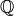 ,
,  ,
, 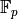 , or anything that can
be converted to
, or anything that can
be converted to  .:
.:
sage: P.<x> = ZZ[]
sage: R.<a> = Zq(27, modulus = x^3 + 2*x + 1); R.modulus()
(1 + O(3^20))*x^3 + (2 + O(3^20))*x + (1 + O(3^20))
sage: P.<x> = QQ[]
sage: S.<a> = Zq(27, modulus = x^3 + 2/7*x + 1)
sage: P.<x> = Zp(3)[]
sage: T.<a> = Zq(27, modulus = x^3 + 2*x + 1)
sage: P.<x> = Qp(3)[]
sage: U.<a> = Zq(27, modulus = x^3 + 2*x + 1)
sage: P.<x> = GF(3)[]
sage: V.<a> = Zq(27, modulus = x^3 + 2*x + 1)
Which form the modulus is given in has no effect on the unramified extension produced:
sage: R == S, R == T, T == U, U == V
(False, True, True, False)
unless the modulus is different, or the precision of the modulus differs. In the case of V, the modulus is only given to precision 1, so the resulting field has a precision cap of 1.:
sage: V.precision_cap()
1
sage: U.precision_cap()
20
sage: P.<x> = Zp(3)[]
sage: modulus = x^3 + (2 + O(3^7))*x + (1 + O(3^10))
sage: modulus
(1 + O(3^20))*x^3 + (2 + O(3^7))*x + (1 + O(3^10))
sage: W.<a> = Zq(27, modulus = modulus); W.precision_cap()
7
The modulus can also be given as a symbolic expression.:
sage: x = var('x')
sage: X.<a> = Zq(27, modulus = x^3 + 2*x + 1); X.modulus()
(1 + O(3^20))*x^3 + (2 + O(3^20))*x + (1 + O(3^20))
sage: X == R
True
By default, the polynomial chosen is the standard lift of the
generator chosen for 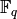 .:
.:
sage: GF(125, 'a').modulus()
x^3 + 3*x + 3
sage: Y.<a> = Zq(125); Y.modulus()
(1 + O(5^20))*x^3 + (3 + O(5^20))*x + (3 + O(5^20))
However, you can choose another polynomial if desired (as long as
the reduction to ![\mathbb{F}_p[x]](../../../_images/math/e5a21492095c9116b100e2f7626a70cc26834e82.png) is irreducible).:
is irreducible).:
sage: P.<x> = ZZ[]
sage: Z.<a> = Zq(125, modulus = x^3 + 3*x^2 + x + 1); Z.modulus()
(1 + O(5^20))*x^3 + (3 + O(5^20))*x^2 + (1 + O(5^20))*x + (1 + O(5^20))
sage: Y == Z
False
PRINTING:
There are many different ways to print  -adic elements. The way
elements of a given field print is controlled by options passed in
at the creation of the field. There are four basic printing modes
('series', 'val-unit', 'terse' and 'bars'; 'digits' is not available), as
well as various options that either hide some information in the
print representation or sometimes make print representations more
compact. Note that the printing options affect whether different
-adic elements. The way
elements of a given field print is controlled by options passed in
at the creation of the field. There are four basic printing modes
('series', 'val-unit', 'terse' and 'bars'; 'digits' is not available), as
well as various options that either hide some information in the
print representation or sometimes make print representations more
compact. Note that the printing options affect whether different
 -adic fields are considered equal.
-adic fields are considered equal.
series: elements are displayed as series in  .:
.:
sage: R.<a> = Zq(9, 20, 'capped-rel', print_mode='series'); (1+2*a)^4
2 + (2*a + 2)*3 + (2*a + 1)*3^2 + O(3^20)
sage: -3*(1+2*a)^4
3 + a*3^2 + 3^3 + (2*a + 2)*3^4 + (2*a + 2)*3^5 + (2*a + 2)*3^6 + (2*a + 2)*3^7 + (2*a + 2)*3^8 + (2*a + 2)*3^9 + (2*a + 2)*3^10 + (2*a + 2)*3^11 + (2*a + 2)*3^12 + (2*a + 2)*3^13 + (2*a + 2)*3^14 + (2*a + 2)*3^15 + (2*a + 2)*3^16 + (2*a + 2)*3^17 + (2*a + 2)*3^18 + (2*a + 2)*3^19 + (2*a + 2)*3^20 + O(3^21)
sage: b = ~(3*a+18); b
(a + 2)*3^-1 + 1 + 2*3 + (a + 1)*3^2 + 3^3 + 2*3^4 + (a + 1)*3^5 + 3^6 + 2*3^7 + (a + 1)*3^8 + 3^9 + 2*3^10 + (a + 1)*3^11 + 3^12 + 2*3^13 + (a + 1)*3^14 + 3^15 + 2*3^16 + (a + 1)*3^17 + 3^18 + O(3^19)
sage: b.parent() is R.fraction_field()
True
print_pos controls whether negatives can be used in the
coefficients of powers of  .:
.:
sage: S.<b> = Zq(9, print_mode='series', print_pos=False); (1+2*b)^4
-1 - b*3 - 3^2 + (b + 1)*3^3 + O(3^20)
sage: -3*(1+2*b)^4
3 + b*3^2 + 3^3 + (-b - 1)*3^4 + O(3^20)
ram_name controls how the prime is printed.:
sage: T.<d> = Zq(9, print_mode='series', ram_name='p'); 3*(1+2*d)^4
2*p + (2*d + 2)*p^2 + (2*d + 1)*p^3 + O(p^20)
print_max_ram_terms limits the number of powers of  that
appear.:
that
appear.:
sage: U.<e> = Zq(9, print_mode='series', print_max_ram_terms=4); repr(-3*(1+2*e)^4)
'3 + e*3^2 + 3^3 + (2*e + 2)*3^4 + ... + O(3^20)'
print_max_unram_terms limits the number of terms that appear in a
coefficient of a power of  .:
.:
sage: V.<f> = Zq(128, prec = 8, print_mode='series'); repr((1+f)^9)
'(f^3 + 1) + (f^5 + f^4 + f^3 + f^2)*2 + (f^6 + f^5 + f^4 + f + 1)*2^2 + (f^5 + f^4 + f^2 + f + 1)*2^3 + (f^6 + f^5 + f^4 + f^3 + f^2 + f + 1)*2^4 + (f^5 + f^4)*2^5 + (f^6 + f^5 + f^4 + f^3 + f + 1)*2^6 + (f + 1)*2^7 + O(2^8)'
sage: V.<f> = Zq(128, prec = 8, print_mode='series', print_max_unram_terms = 3); repr((1+f)^9)
'(f^3 + 1) + (f^5 + f^4 + ... + f^2)*2 + (f^6 + f^5 + ... + 1)*2^2 + (f^5 + f^4 + ... + 1)*2^3 + (f^6 + f^5 + ... + 1)*2^4 + (f^5 + f^4)*2^5 + (f^6 + f^5 + ... + 1)*2^6 + (f + 1)*2^7 + O(2^8)'
sage: V.<f> = Zq(128, prec = 8, print_mode='series', print_max_unram_terms = 2); repr((1+f)^9)
'(f^3 + 1) + (f^5 + ... + f^2)*2 + (f^6 + ... + 1)*2^2 + (f^5 + ... + 1)*2^3 + (f^6 + ... + 1)*2^4 + (f^5 + f^4)*2^5 + (f^6 + ... + 1)*2^6 + (f + 1)*2^7 + O(2^8)'
sage: V.<f> = Zq(128, prec = 8, print_mode='series', print_max_unram_terms = 1); repr((1+f)^9)
'(f^3 + ...) + (f^5 + ...)*2 + (f^6 + ...)*2^2 + (f^5 + ...)*2^3 + (f^6 + ...)*2^4 + (f^5 + ...)*2^5 + (f^6 + ...)*2^6 + (f + ...)*2^7 + O(2^8)'
sage: V.<f> = Zq(128, prec = 8, print_mode='series', print_max_unram_terms = 0); repr((1+f)^9 - 1 - f^3)
'(...)*2 + (...)*2^2 + (...)*2^3 + (...)*2^4 + (...)*2^5 + (...)*2^6 + (...)*2^7 + O(2^8)'
print_sep and print_max_terse_terms have no effect.
Note that print options affect equality:
sage: R == S, R == T, R == U, R == V, S == T, S == U, S == V, T == U, T == V, U == V
(False, False, False, False, False, False, False, False, False, False)
val-unit: elements are displayed as 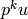 :
:
sage: R.<a> = Zq(9, 7, print_mode='val-unit'); b = (1+3*a)^9 - 1; b
3^3 * (15 + 64*a) + O(3^7)
sage: ~b
3^-3 * (41 + a) + O(3)
print_pos controls whether to use a balanced representation or not.:
sage: S.<a> = Zq(9, 7, print_mode='val-unit', print_pos=False); b = (1+3*a)^9 - 1; b
3^3 * (15 - 17*a) + O(3^7)
sage: ~b
3^-3 * (-40 + a) + O(3)
ram_name affects how the prime is printed.:
sage: A.<x> = Zp(next_prime(10^6), print_mode='val-unit')[]
sage: T.<a> = Zq(next_prime(10^6)^3, 4, print_mode='val-unit', ram_name='p', modulus=x^3+385831*x^2+106556*x+321036); b = (next_prime(10^6)^2*(a^2 + a - 4)^4); b
p^2 * (90732455187 + 713749771767*a + 579958835561*a^2) + O(p^4)
sage: b * (a^2 + a - 4)^-4
p^2 * 1 + O(p^4)
print_max_terse_terms controls how many terms of the polynomial appear in the unit part.:
sage: U.<a> = Zq(17^4, 6, print_mode='val-unit', print_max_terse_terms=3); b = (17*(a^3-a+14)^6); b
17 * (772941 + 717522*a + 870707*a^2 + ...) + O(17^6)
print_sep, print_max_ram_terms and print_max_unram_terms have no effect.
Equality again depends on the printing options:
sage: R == S, R == T, R == U, S == T, S == U, T == U
(False, False, False, False, False, False)
terse: elements are displayed as a polynomial of degree less than the degree of the extension.:
sage: R.<a> = Zq(125, print_mode='terse')
sage: (a+5)^177
68210977979428 + 90313850704069*a + 73948093055069*a^2 + O(5^20)
sage: (a/5+1)^177
10990518995053/5^177 + 14019905391569/5^177*a + 16727634070694/5^177*a^2 + O(5^-158)
Note that in this last computation, you get one fewer  -adic digit
than one might expect. This is because R is capped absolute, and
thus 5 is cast in with relative precision 19.
-adic digit
than one might expect. This is because R is capped absolute, and
thus 5 is cast in with relative precision 19.
As of version 3.3, if coefficients of the polynomial are
non-integral, they are always printed with an explicit power of  in the denominator.:
in the denominator.:
sage: 5*a + a^2/25
5*a + 1/5^2*a^2 + O(5^16)
print_pos controls whether to use a balanced representation or not.:
sage: (a-5)^6
22864 + 95367431627998*a + 8349*a^2 + O(5^20)
sage: S.<a> = Zq(125, print_mode='terse', print_pos=False); b = (a-5)^6; b
22864 - 12627*a + 8349*a^2 + O(5^20)
sage: (a - 1/5)^6
-20624/5^6 + 18369/5^5*a + 1353/5^3*a^2 + O(5^14)
ram_name affects how the prime is printed.:
sage: T.<a> = Zq(125, print_mode='terse', ram_name='p'); (a - 1/5)^6
95367431620001/p^6 + 18369/p^5*a + 1353/p^3*a^2 + O(p^14)
print_max_terse_terms controls how many terms of the polynomial are shown.:
sage: U.<a> = Zq(625, print_mode='terse', print_max_terse_terms=2); (a-1/5)^6
106251/5^6 + 49994/5^5*a + ... + O(5^14)
print_sep, print_max_ram_terms and print_max_unram_terms have no effect.
Equality again depends on the printing options:
sage: R == S, R == T, R == U, S == T, S == U, T == U
(False, False, False, False, False, False)
digits: This print mode is not available when the residue field is not prime. It might make sense to have a dictionary for small fields, but this isn’t implemented.
bars: elements are displayed in a similar fashion to series, but more compactly.:
sage: R.<a> = Zq(125); (a+5)^6
(4*a^2 + 3*a + 4) + (3*a^2 + 2*a)*5 + (a^2 + a + 1)*5^2 + (3*a + 2)*5^3 + (3*a^2 + a + 3)*5^4 + (2*a^2 + 3*a + 2)*5^5 + O(5^20)
sage: R.<a> = Zq(125, print_mode='bars', prec=8); repr((a+5)^6)
'...[2, 3, 2]|[3, 1, 3]|[2, 3]|[1, 1, 1]|[0, 2, 3]|[4, 3, 4]'
sage: repr((a-5)^6)
'...[0, 4]|[1, 4]|[2, 0, 2]|[1, 4, 3]|[2, 3, 1]|[4, 4, 3]|[2, 4, 4]|[4, 3, 4]'
Note that it’s not possible to read of the precision from the representation in this mode.:
sage: b = a + 3; repr(b)
'...[3, 1]'
sage: c = a + R(3, 4); repr(c)
'...[3, 1]'
sage: b.precision_absolute()
8
sage: c.precision_absolute()
4
print_pos controls whether the digits can be negative.:
sage: S.<a> = Zq(125, print_mode='bars', print_pos=False); repr((a-5)^6)
'...[1, -1, 1]|[2, 1, -2]|[2, 0, -2]|[-2, -1, 2]|[0, 0, -1]|[-2]|[-1, -2, -1]'
sage: repr((a-1/5)^6)
'...[0, 1, 2]|[-1, 1, 1]|.|[-2, -1, -1]|[2, 2, 1]|[0, 0, -2]|[0, -1]|[0, -1]|[1]'
print_max_ram_terms controls the maximum number of “digits” shown. Note that this puts a cap on the relative precision, not the absolute precision.:
sage: T.<a> = Zq(125, print_mode='bars', print_max_ram_terms=3, print_pos=False); repr((a-5)^6)
'...[0, 0, -1]|[-2]|[-1, -2, -1]'
sage: repr(5*(a-5)^6+50)
'...[0, 0, -1]|[]|[-1, -2, -1]|[]'
However, if the element has negative valuation, digits are shown up to the decimal point.:
sage: repr((a-1/5)^6)
'...|.|[-2, -1, -1]|[2, 2, 1]|[0, 0, -2]|[0, -1]|[0, -1]|[1]'
print_sep controls the separating character ('|' by default).:
sage: U.<a> = Zq(625, print_mode='bars', print_sep=''); b = (a+5)^6; repr(b)
'...[0, 1][4, 0, 2][3, 2, 2, 3][4, 2, 2, 4][0, 3][1, 1, 3][3, 1, 4, 1]'
print_max_unram_terms controls how many terms are shown in each 'digit':
sage: with local_print_mode(U, {'max_unram_terms': 3}): repr(b)
'...[0, 1][4,..., 0, 2][3,..., 2, 3][4,..., 2, 4][0, 3][1,..., 1, 3][3,..., 4, 1]'
sage: with local_print_mode(U, {'max_unram_terms': 2}): repr(b)
'...[0, 1][4,..., 2][3,..., 3][4,..., 4][0, 3][1,..., 3][3,..., 1]'
sage: with local_print_mode(U, {'max_unram_terms': 1}): repr(b)
'...[..., 1][..., 2][..., 3][..., 4][..., 3][..., 3][..., 1]'
sage: with local_print_mode(U, {'max_unram_terms':0}): repr(b-75*a)
'...[...][...][...][...][][...][...]'
ram_name and print_max_terse_terms have no effect.
Equality depends on printing options:
sage: R == S, R == T, R == U, S == T, S == U, T == U
(False, False, False, False, False, False)
EXAMPLES
Unlike for Zp, you can’t create Zq(N) when N is not a prime power.
However, you can use check=False to pass in a pair in order to not have to factor. If you do so, you need to use names explicitly rather than the R.<a> syntax.:
sage: p = next_prime(2^123)
sage: k = Zp(p)
sage: R.<x> = k[]
sage: K = Zq([(p, 5)], modulus=x^5+x+4, names='a', ram_name='p', print_pos=False, check=False)
sage: K.0^5
(-a - 4) + O(p^20)
In tests on sage.math, the creation of K as above took an average of 1.58ms, while:
sage: K = Zq(p^5, modulus=x^5+x+4, names='a', ram_name='p', print_pos=False, check=True)
took an average of 24.5ms. Of course, with smaller primes these savings disappear.
A shortcut function to create capped absolute unramified  -adic rings.
-adic rings.
See documentation for Zq for a description of the input parameters.
EXAMPLES:
sage: R.<a> = ZqCA(25, 40); R
Unramified Extension of 5-adic Ring with capped absolute precision 40 in a defined by (1 + O(5^40))*x^2 + (4 + O(5^40))*x + (2 + O(5^40))
A shortcut function to create capped relative unramified  -adic rings.
-adic rings.
Same functionality as Zq. See documentation for Zq for a description of the input parameters.
EXAMPLES:
sage: R.<a> = ZqCR(25, 40); R
Unramified Extension of 5-adic Ring with capped relative precision 40 in a defined by (1 + O(5^40))*x^2 + (4 + O(5^40))*x + (2 + O(5^40))
A shortcut function to create fixed modulus unramified  -adic rings.
-adic rings.
See documentation for Zq for a description of the input parameters.
EXAMPLES:
sage: R.<a> = ZqFM(25, 40); R
Unramified Extension of 5-adic Ring of fixed modulus 5^40 in a defined by (1 + O(5^40))*x^2 + (4 + O(5^40))*x + (2 + O(5^40))
Returns True iff this monic polynomial is Eisenstein.
A polynomial is Eisenstein if it is monic, the constant term has valuation 1 and all other terms have positive valuation.
EXAMPLES:
sage: R = Zp(5)
sage: S.<x> = R[]
sage: from sage.rings.padics.factory import is_eisenstein
sage: f = x^4 - 75*x + 15
sage: is_eisenstein(f)
True
sage: g = x^4 + 75
sage: is_eisenstein(g)
False
sage: h = x^7 + 27*x -15
sage: is_eisenstein(h)
False
Returns true iff this monic polynomial is unramified.
A polynomial is unramified if its reduction modulo the maximal ideal is irreducible.
EXAMPLES:
sage: R = Zp(5)
sage: S.<x> = R[]
sage: from sage.rings.padics.factory import is_unramified
sage: f = x^4 + 14*x + 9
sage: is_unramified(f)
True
sage: g = x^6 + 17*x + 6
sage: is_unramified(g)
False
Returns True iff poly determines a unique isomorphism class of extensions at precision prec.
Currently just returns True (thus allowing extensions that are not defined to high enough precision in order to specify them up to isomorphism). This will change in the future.
EXAMPLES:
sage: from sage.rings.padics.factory import krasner_check
sage: krasner_check(1,2) #this is a stupid example.
True
Bases: sage.structure.factory.UniqueFactory
A class for creating extensions of  -adic rings and fields.
-adic rings and fields.
EXAMPLES:
sage: R = Zp(5,3)
sage: S.<x> = ZZ[]
sage: W.<w> = pAdicExtension(R, x^4-15)
sage: W
Eisenstein Extension of 5-adic Ring with capped relative precision 3 in w defined by (1 + O(5^3))*x^4 + (O(5^4))*x^3 + (O(5^4))*x^2 + (O(5^4))*x + (2*5 + 4*5^2 + 4*5^3 + O(5^4))
sage: W.precision_cap()
12
Creates a key from input parameters for pAdicExtension.
See the documentation for Qq for more information.
TESTS:
sage: R = Zp(5,3)
sage: S.<x> = ZZ[]
sage: pAdicExtension.create_key_and_extra_args(R, x^4-15,names='w')
(('e', 5-adic Ring with capped relative precision 3, x^4 - 15, (1 + O(5^3))*x^4 + (O(5^4))*x^3 + (O(5^4))*x^2 + (O(5^4))*x + (2*5 + 4*5^2 + 4*5^3 + O(5^4)), ('w', None, None, 'w'), 12, None, 'series', True, '|', ('0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z'), -1, -1, -1), {'shift_seed': (3 + O(5^3))})
Creates an object using a given key.
See the documentation for pAdicExtension for more information.
TESTS:
sage: R = Zp(5,3)
sage: S.<x> = R[]
sage: pAdicExtension.create_object(version = (3,4,2), key = ('e', R, x^4 - 15, x^4 - 15, ('w', None, None, 'w'), 12, None, 'series', True, '|', ('0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z'),-1,-1,-1), shift_seed = S(3 + O(5^3)))
Eisenstein Extension of 5-adic Ring with capped relative precision 3 in w defined by (1 + O(5^3))*x^4 + (2*5 + 4*5^2 + 4*5^3 + O(5^4))
Truncates the unused precision off of a polynomial.
EXAMPLES:
sage: R = Zp(5)
sage: S.<x> = R[]
sage: from sage.rings.padics.factory import truncate_to_prec
sage: f = x^4 + (3+O(5^6))*x^3 + O(5^4)
sage: truncate_to_prec(f, 5)
(1 + O(5^5))*x^4 + (3 + O(5^5))*x^3 + (O(5^5))*x^2 + (O(5^5))*x + (O(5^4))