Unit Groups of Number Fields

EXAMPLES:

sage: x = polygen(QQ)
sage: K.<a> = NumberField(x^4-8*x^2+36)
sage: UK = UnitGroup(K); UK
Unit group with structure C4 x Z of Number Field in a with defining polynomial x^4 - 8*x^2 + 36

The first generator is a primitive root of unity in the field:

sage: UK.gens() # random
[1/12*a^3 - 1/6*a, 1/24*a^3 + 1/4*a^2 - 1/12*a - 1]
sage: [u.multiplicative_order() for u in UK.gens()]
[4, +Infinity]

sage: UK.rank()
1
sage: UK.ngens()
2

Units in the field can be converted into elements of the unit group represented as elements of an abstract multiplicative group:

sage: UK(1)
1
sage: UK(-1)
u0^2
sage: [UK(u) for u in (x^4-1).roots(K,multiplicities=False)]
[1, u0^2, u0, u0^3]

sage: UK.fundamental_units() # random
[1/24*a^3 + 1/4*a^2 - 1/12*a - 1]
sage: UK.torsion_generator()
1/12*a^3 - 1/6*a
sage: UK.zeta_order()
4
sage: UK.roots_of_unity()
[1/12*a^3 - 1/6*a, -1, -1/12*a^3 + 1/6*a, 1]

Exp and log functions provide maps between units as field elements and exponent vectors with respect to the generators:

sage: u = UK.exp([13,10]); u # random
-41/8*a^3 - 55/4*a^2 + 41/4*a + 55
sage: UK.log(u)
[1, 10]
sage: u = UK.fundamental_units()[0]
sage: [UK.log(u^k) == [0,k] for k in range(10)]
[True, True, True, True, True, True, True, True, True, True]
sage: all([UK.log(u^k) == [0,k] for k in range(10)])
True

sage: K.<a> = NumberField(x^5-2,'a')
sage: UK = UnitGroup(K)
sage: UK.rank()
2
sage: UK.fundamental_units()
[a^3 + a^2 - 1, a - 1]    

A relative number field example:

sage: L.<a, b> = NumberField([x^2 + x + 1, x^4 + 1])
sage: UL = L.unit_group(); UL
Unit group with structure C24 x Z x Z x Z of Number Field in a with defining polynomial x^2 + x + 1 over its base field
sage: UL.gens() # random
[-b^3*a - b^3, -b^3*a + b, (-b^3 - b^2 - b)*a - b - 1, (-b^3 - 1)*a - b^2 + b - 1]
sage: UL.zeta_order()
24
sage: UL.roots_of_unity()
[-b^3*a - b^3,
-b^2*a,
b,
a + 1,
-b^3*a,
b^2,
b*a + b,
a,
b^3,
b^2*a + b^2,
b*a,
-1,
b^3*a + b^3,
b^2*a,
-b,
-a - 1,
b^3*a,
-b^2,
-b*a - b,
-a,
-b^3,
-b^2*a - b^2,
-b*a,
1]

A relative extension example, which worked thanks to the code review by F.W.Clarke:

sage: PQ.<X> = QQ[]
sage: F.<a, b> = NumberField([X^2 - 2, X^2 - 3])
sage: PF.<Y> = F[]
sage: K.<c> = F.extension(Y^2 - (1 + a)*(a + b)*a*b)
sage: K.unit_group()
Unit group with structure C2 x Z x Z x Z x Z x Z x Z x Z of Number Field in c with defining polynomial Y^2 + (-2*b - 3)*a - 2*b - 6 over its base field

AUTHOR:

• John Cremona

class sage.rings.number_field.unit_group.UnitGroup(number_field, proof=True)

Bases: sage.groups.abelian_gps.abelian_group.AbelianGroup_class

The unit group of a number field.

exp(exponents)

Return unit with given exponents with respect to group generators.

INPUT:

• u – Any object from which an element of the unit group’s number field may be constructed; an error is raised if an element of cannot be constructed from u, or if the element constructed is not a unit.

OUTPUT: a list of integers giving the exponents of u with respect to the unit group’s basis.

EXAMPLES:

sage: x = polygen(QQ)
sage: K.<z> = CyclotomicField(13)
sage: UK = UnitGroup(K)
sage: [UK.log(u) for u in UK.gens()]
[[1, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 1]]
sage: vec = [65,6,7,8,9,10]
sage: unit = UK.exp(vec)
sage: UK.log(unit)
[13, 6, 7, 8, 9, 10]
sage: UK.exp(UK.log(u)) == u
True

fundamental_units()

Return generators for the free part of the unit group, as a list.

EXAMPLES:

sage: x = polygen(QQ)
sage: K.<a> = NumberField(x^4 + 23)
sage: U = UnitGroup(K)
sage: U.fundamental_units()  # random
[1/4*a^3 - 7/4*a^2 + 17/4*a - 19/4]

gen(i=0)

Return the ‘th generator for this unit group.

Note

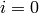gives the torsion generator, i.e. a primitive root of unity.

EXAMPLES:

sage: K.<z> = CyclotomicField(13)
sage: UK = K.unit_group()
sage: UK.ngens()
6
sage: UK.gen(0) # random
-z^11
sage: UK.gen(1) # random
z^5 + z^3
sage: UK.gen(2) # random
z^6 + z^5
sage: UK.gen(3) # random
z^9 + z^7 + z^5
sage: UK.gen(4) # random
z^9 + z^5 + z^4 + 1
sage: UK.gen(5) # random
z^5 + z

gens()

Return generators for the unit group, as a list.

EXAMPLES:

sage: x = polygen(QQ)
sage: K.<a> = NumberField(x^4 + 23)
sage: K.unit_group().gens() # random
[-1, 1/4*a^3 - 7/4*a^2 + 17/4*a - 19/4]

log(u)

Return the exponents of the unit u with respect to group generators.

INPUT:

• u – Any object from which an element of the unit group’s number field may be constructed; an error is raised if an element of cannot be constructed from u, or if the element constructed is not a unit.

OUTPUT: a list of integers giving the exponents of u with respect to the unit group’s basis.

EXAMPLES:

sage: x = polygen(QQ)
sage: K.<z> = CyclotomicField(13)
sage: UK = UnitGroup(K)
sage: [UK.log(u) for u in UK.gens()]
[[1, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 1]]
sage: vec = [65,6,7,8,9,10]
sage: unit = UK.exp(vec); unit
-253576*z^11 + 7003*z^10 - 395532*z^9 - 35275*z^8 - 500326*z^7 - 35275*z^6 - 395532*z^5 + 7003*z^4 - 253576*z^3 - 59925*z - 59925
sage: UK.log(unit)
[13, 6, 7, 8, 9, 10]

ngens()

Return the number of generators of the unit group.

EXAMPLES:

sage: x = polygen(QQ)
sage: U = NumberField(x^2 + x + 23899, 'a').unit_group(); U
Unit group with structure C2 of Number Field in a with defining polynomial x^2 + x + 23899
sage: U.ngens()
1

number_field()

Return the number field associated with this unit group.

EXAMPLES:

sage: x = polygen(QQ)
sage: U = UnitGroup(NumberField(x^2 + 23, 'w')); U
Unit group with structure C2 of Number Field in w with defining polynomial x^2 + 23
sage: U.number_field()
Number Field in w with defining polynomial x^2 + 23

rank()

Return the rank of the unit group.

EXAMPLES:

sage: K.<z> = CyclotomicField(13)
sage: UnitGroup(K).rank()
5

roots_of_unity()

Return all the roots of unity in this unit group, primitive or not.

EXAMPLES:

sage: x = polygen(QQ)
sage: K.<b> = NumberField(x^2+1)
sage: U = UnitGroup(K)
sage: zs = U.roots_of_unity(); zs
[b, -1, -b, 1]
sage: [ z**U.zeta_order() for z in zs ]
[1, 1, 1, 1]

torsion_generator()

Return a generator for the torsion part of the unit group.

EXAMPLES:

sage: x = polygen(QQ)
sage: K.<a> = NumberField(x^4 - x^2 + 4)
sage: U = UnitGroup(K)
sage: U.torsion_generator() # random
-1/4*a^3 - 1/4*a + 1/2

zeta(n=2, all=False)

Return one, or a list of all, primitive n-th root of unity in this unit group.

EXAMPLES:

sage: x = polygen(QQ)
sage: K.<z> = NumberField(x^2 + 3)
sage: U = UnitGroup(K)
sage: U.zeta(1)
1
sage: U.zeta(2)
-1
sage: U.zeta(2, all=True)
[-1]
sage: U.zeta(3)
-1/2*z - 1/2
sage: U.zeta(3, all=True)
[-1/2*z - 1/2, 1/2*z - 1/2]
sage: U.zeta(4)
...
ValueError: n (=4) does not divide order of generator

sage: r.<x> = QQ[]
sage: K.<b> = NumberField(x^2+1)
sage: U = UnitGroup(K)
sage: U.zeta(4)
b
sage: U.zeta(4,all=True)
[b, -b]
sage: U.zeta(3)
...
ValueError: n (=3) does not divide order of generator
sage: U.zeta(3,all=True)
[]

zeta_order()

Returns the order of the torsion part of the unit group.

EXAMPLES:

sage: x = polygen(QQ)
sage: K.<a> = NumberField(x^4 - x^2 + 4)
sage: U = UnitGroup(K)
sage: U.zeta_order()
6