AUTHORS:
TODO:
Background on invariant factors and the Smith normal form
(according to section 4.1 of [C1]): An abelian group is a
group A for which there exists an exact sequence
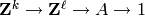 ,
for some positive integers
,
for some positive integers
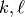 with
with 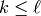 . For example, a finite abelian group has a
decomposition
. For example, a finite abelian group has a
decomposition
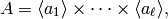
where 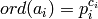 , for some primes
, for some primes 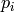 and some
positive integers
and some
positive integers 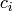 ,
, 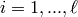 . GAP calls the
list (ordered by size) of the
. GAP calls the
list (ordered by size) of the  the abelian invariants.
In Sage they will be called invariants.
In this situation,
the abelian invariants.
In Sage they will be called invariants.
In this situation, 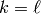 and
and 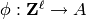 is the map
is the map
 ,
for
,
for  . The matrix of relations
. The matrix of relations
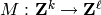 is the matrix
whose rows generate the kernel of
is the matrix
whose rows generate the kernel of 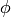 as a
as a  -module.
In other words,
-module.
In other words, 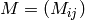 is a
is a 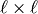 diagonal matrix with
diagonal matrix with 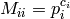 . Consider now the
subgroup
. Consider now the
subgroup 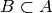 generated by
generated by
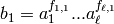 , ...,
, ...,
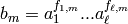 .
The kernel of the map
.
The kernel of the map 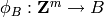 defined by
defined by
 ,
for
,
for 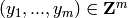 , is the kernel of the matrix
, is the kernel of the matrix
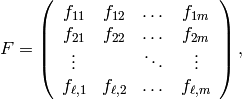
regarded as a map
 .
In particular,
.
In particular,  . If
. If  then the
Smith normal form (SNF) of a generator matrix of
then the
Smith normal form (SNF) of a generator matrix of
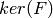 and the SNF of
and the SNF of 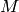 are the same. The diagonal entries
are the same. The diagonal entries 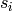 of the
SNF
of the
SNF ![S = diag[s_1,s_2,s_3, ... s_r,0,0,...0]](../../../_images/math/2689afe347a2a8396336118b2d78260c564e5c40.png) ,
are called determinantal divisors of
,
are called determinantal divisors of 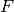 .
where
.
where  is the rank. The {it invariant factors} of A are:
is the rank. The {it invariant factors} of A are:

Sage supports multiplicative abelian groups on any prescribed finite
number 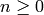 of generators. Use the AbelianGroup function
to create an abelian group, and the gen and gens
functions to obtain the corresponding generators. You can print the
generators as arbitrary strings using the optional names
argument to the AbelianGroup function.
of generators. Use the AbelianGroup function
to create an abelian group, and the gen and gens
functions to obtain the corresponding generators. You can print the
generators as arbitrary strings using the optional names
argument to the AbelianGroup function.
EXAMPLE 1:
We create an abelian group in zero or more variables; the syntax T(1) creates the identity element even in the rank zero case.
sage: T = AbelianGroup(0,[])
sage: T
Trivial Abelian Group
sage: T.gens()
()
sage: T(1)
1
EXAMPLE 2: An abelian group uses a multiplicative representation of elements, but the underlying representation is lists of integer exponents.
sage: F = AbelianGroup(5,[3,4,5,5,7],names = list("abcde"))
sage: F
Multiplicative Abelian Group isomorphic to C3 x C4 x C5 x C5 x C7
sage: (a,b,c,d,e) = F.gens()
sage: a*b^2*e*d
a*b^2*d*e
sage: x = b^2*e*d*a^7
sage: x
a*b^2*d*e
sage: x.list()
[1, 2, 0, 1, 1]
REFERENCES:
Warning
Many basic properties for infinite abelian groups are not implemented.
Create the multiplicative abelian group in  generators
with given invariants (which need not be prime powers).
generators
with given invariants (which need not be prime powers).
INPUT:
n - integer
invfac - (the”invariant factors”) a list of non-negative integers in the form [a0, a1,...,a(n-1)], typically written in increasing order. This list is padded with zeros if it has length less than n.
names - (optional) names of generators
Alternatively, you can also give input in the following form:
AbelianGroup(invfac, names="f"),
where names must be explicitly named.
OUTPUT: Abelian group with generators and invariant type. The default name for generator A.i is fi, as in GAP.
EXAMPLES:
sage: F = AbelianGroup(5, [5,5,7,8,9], names='abcde')
sage: F(1)
1
sage: (a, b, c, d, e) = F.gens()
sage: mul([ a, b, a, c, b, d, c, d ], F(1))
a^2*b^2*c^2*d^2
sage: d * b**2 * c**3
b^2*c^3*d
sage: F = AbelianGroup(3,[2]*3); F
Multiplicative Abelian Group isomorphic to C2 x C2 x C2
sage: H = AbelianGroup([2,3], names="xy"); H
Multiplicative Abelian Group isomorphic to C2 x C3
sage: AbelianGroup(5)
Multiplicative Abelian Group isomorphic to Z x Z x Z x Z x Z
sage: AbelianGroup(5).order()
+Infinity
Notice how  ‘s are padded on.
‘s are padded on.
sage: AbelianGroup(5, [2,3,4])
Multiplicative Abelian Group isomorphic to Z x Z x C2 x C3 x C4
The invariant list can’t be longer than the number of generators.
sage: AbelianGroup(2, [2,3,4])
...
ValueError: invfac (=[2, 3, 4]) must have length n (=2)
Bases: sage.groups.group.AbelianGroup
Abelian group on  generators. The invariant factors
generators. The invariant factors
![[a_1,a_2,...,a_k]](../../../_images/math/ba8416b22ddddda62b53d87079df5e68b13b4280.png) need not be prime powers.
divisors will be).
need not be prime powers.
divisors will be).
EXAMPLES:
sage: F = AbelianGroup(5,[5,5,7,8,9],names = list("abcde")); F
Multiplicative Abelian Group isomorphic to C5 x C5 x C7 x C8 x C9
sage: F = AbelianGroup(5,[2, 4, 12, 24, 120],names = list("abcde")); F
Multiplicative Abelian Group isomorphic to C2 x C4 x C12 x C24 x C120
sage: F.elementary_divisors()
[2, 4, 12, 24, 120]
The entry 1 in the list of invariants is ignored:
sage: F = AbelianGroup(3,[1,2,3],names='a')
sage: F.invariants()
[2, 3]
sage: F.gens()
(a0, a1)
sage: F.ngens()
2
sage: (F.0).order()
2
sage: (F.1).order()
3
sage: AbelianGroup(1, [1], names='e')
Multiplicative Abelian Group isomorphic to C1
sage: AbelianGroup(1, [1], names='e').gens()
(e,)
sage: AbelianGroup(1, [1], names='e').list()
[1]
sage: AbelianGroup(3, [2, 1, 2], names=list('abc')).list()
[1, b, a, a*b]
sage: F.category()
Category of groups
Returns the dual group.
EXAMPLES:
This returns the elementary divisors of the group, using Pari.
Note
Here is another algorithm for computing the elementary divisors
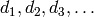 , of a finite abelian group (where
, of a finite abelian group (where 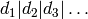 are composed of prime powers dividing the invariants of the group
in a way described below). Just factor the invariants
are composed of prime powers dividing the invariants of the group
in a way described below). Just factor the invariants 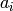 that
define the abelian group. Then the biggest
that
define the abelian group. Then the biggest 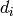 is the product
of the maximum prime powers dividing some
is the product
of the maximum prime powers dividing some 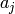 . In other words, the
largest
. In other words, the
largest 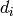 is the product of
is the product of  , where
, where 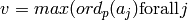 ).
Now divide out all those
).
Now divide out all those  ‘s into the list of invariants
‘s into the list of invariants 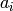 ,
and get a new list of “smaller invariants”“. Repeat the above procedure
on these “”smaller invariants”” to compute
,
and get a new list of “smaller invariants”“. Repeat the above procedure
on these “”smaller invariants”” to compute 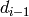 , and so on.
(Thanks to Robert Miller for communicating this algorithm.)
, and so on.
(Thanks to Robert Miller for communicating this algorithm.)
EXAMPLES:
sage: G = AbelianGroup(2,[2,3])
sage: G.elementary_divisors()
[6]
sage: G = AbelianGroup(1, [6])
sage: G.elementary_divisors()
[6]
sage: G = AbelianGroup(2,[2,6])
sage: G
Multiplicative Abelian Group isomorphic to C2 x C6
sage: G.invariants()
[2, 6]
sage: G.elementary_divisors()
[2, 6]
sage: J = AbelianGroup([1,3,5,12])
sage: J.elementary_divisors()
[3, 60]
sage: G = AbelianGroup(2,[0,6])
sage: G.elementary_divisors()
[6, 0]
Return the exponent of this abelian group.
EXAMPLES:
sage: G = AbelianGroup([2,3,7]); G
Multiplicative Abelian Group isomorphic to C2 x C3 x C7
sage: G.exponent()
42
sage: G = AbelianGroup([2,4,6]); G
Multiplicative Abelian Group isomorphic to C2 x C4 x C6
sage: G.exponent()
12
The  -th generator of the abelian group.
-th generator of the abelian group.
EXAMPLES:
sage: F = AbelianGroup(5,[],names='a')
sage: F.0
a0
sage: F.2
a2
sage: F.invariants()
[0, 0, 0, 0, 0]
Return the identity element of this group.
EXAMPLES:
sage: G = AbelianGroup([2,2])
sage: e = G.identity()
sage: e
1
sage: g = G.gen(0)
sage: g*e
f0
sage: e*g
f0
Return a copy of the list of invariants of this group.
It is safe to modify the returned list.
EXAMPLES:
sage: J = AbelianGroup([2,3])
sage: J.invariants()
[2, 3]
sage: v = J.invariants(); v
[2, 3]
sage: v[0] = 5
sage: J.invariants()
[2, 3]
sage: J.invariants() is J.invariants()
False
Return True since this group is commutative.
EXAMPLES:
sage: G = AbelianGroup([2,3,9, 0])
sage: G.is_commutative()
True
sage: G.is_abelian()
True
Return True if the group is a cyclic group.
Return list of all elements of this group.
EXAMPLES:
sage: G = AbelianGroup([2,3], names = "ab")
sage: G.list()
[1, b, b^2, a, a*b, a*b^2]
sage: G = AbelianGroup([]); G
Trivial Abelian Group
sage: G.list()
[1]
The number of free generators of the abelian group.
EXAMPLES:
sage: F = AbelianGroup(10000)
sage: F.ngens()
10000
Return the order of this group.
EXAMPLES:
sage: G = AbelianGroup(2,[2,3])
sage: G.order()
6
sage: G = AbelianGroup(3,[2,3,0])
sage: G.order()
+Infinity
Return the permutation group isomorphic to this abelian group.
If the invariants are 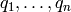 then the
generators of the permutation will be of order
then the
generators of the permutation will be of order
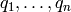 , respectively.
, respectively.
EXAMPLES:
sage: G = AbelianGroup(2,[2,3]); G
Multiplicative Abelian Group isomorphic to C2 x C3
sage: G.permutation_group()
Permutation Group with generators [(1,4)(2,5)(3,6), (1,2,3)(4,5,6)]
Return a random element of this group. (Renamed random to random_element.)
EXAMPLES:
sage: G = AbelianGroup([2,3,9])
sage: G.random_element()
f0*f1^2*f2
Create a subgroup of this group. The “big” group must be defined using “named” generators.
INPUT:
EXAMPLES:
sage: G.<a,b,c> = AbelianGroup(3, [2,3,4]); G
Multiplicative Abelian Group isomorphic to C2 x C3 x C4
sage: H = G.subgroup([a*b,a]); H
Multiplicative Abelian Group isomorphic to C2 x C3, which is the subgroup of
Multiplicative Abelian Group isomorphic to C2 x C3 x C4
generated by [a*b, a]
sage: H < G
True
sage: F = G.subgroup([a,b^2])
sage: F
Multiplicative Abelian Group isomorphic to C2 x C3, which is the subgroup of
Multiplicative Abelian Group isomorphic to C2 x C3 x C4
generated by [a, b^2]
sage: F.gens()
[a, b^2]
sage: F = AbelianGroup(5,[30,64,729],names = list("abcde"))
sage: a,b,c,d,e = F.gens()
sage: F.subgroup([a,b])
Multiplicative Abelian Group isomorphic to Z x Z, which is
the subgroup of Multiplicative Abelian Group isomorphic to
Z x Z x C30 x C64 x C729 generated by [a, b]
sage: F.subgroup([c,e])
Multiplicative Abelian Group isomorphic to C2 x C3 x C5 x
C729, which is the subgroup of Multiplicative Abelian
Group isomorphic to Z x Z x C30 x C64 x C729 generated by
[c, e]
Given a list of lists of integers (corresponding to elements of self), find a set of independent generators for the subgroup generated by these elements, and return the subgroup with these as generators, forgetting the original generators.
This is used by the subgroups routine.
An error will be raised if the elements given are not linearly independent over QQ.
EXAMPLE:
sage: G = AbelianGroup([4,4])
sage: G.subgroup( [ G([1,0]), G([1,2]) ])
Multiplicative Abelian Group isomorphic to C2 x C4, which is the subgroup of
Multiplicative Abelian Group isomorphic to C4 x C4
generated by [f0, f0*f1^2]
sage: AbelianGroup([4,4]).subgroup_reduced( [ [1,0], [1,2] ])
Multiplicative Abelian Group isomorphic to C2 x C4, which is the subgroup of
Multiplicative Abelian Group isomorphic to C4 x C4
generated by [f1^2, f0]
Compute all the subgroups of this abelian group (which must be finite).
TODO: This is many orders of magnitude slower than Magma.
INPUT:
ALGORITHM:
If the group is cyclic, the problem is easy. Otherwise, write it as a direct product A x B, where B is cyclic. Compute the subgroups of A (by recursion).
Now, for every subgroup C of A x B, let G be its projection onto A and H its intersection with B. Then there is a well-defined homomorphism f: G -> B/H that sends a in G to the class mod H of b, where (a,b) is any element of C lifting a; and every subgroup C arises from a unique triple (G, H, f).
EXAMPLES:
sage: AbelianGroup([2,3]).subgroups()
[Multiplicative Abelian Group isomorphic to C2 x C3, which is the subgroup of
Multiplicative Abelian Group isomorphic to C2 x C3
generated by [f0*f1^2],
Multiplicative Abelian Group isomorphic to C2, which is the subgroup of
Multiplicative Abelian Group isomorphic to C2 x C3
generated by [f0],
Multiplicative Abelian Group isomorphic to C3, which is the subgroup of
Multiplicative Abelian Group isomorphic to C2 x C3
generated by [f1],
Trivial Abelian Group, which is the subgroup of
Multiplicative Abelian Group isomorphic to C2 x C3
generated by []]
sage: len(AbelianGroup([2,4,8]).subgroups())
81
Bases: sage.groups.abelian_gps.abelian_group.AbelianGroup_class
Subgroup subclass of AbelianGroup_class, so instance methods are inherited.
TODO:
Return the nth generator of this subgroup.
EXAMPLE:
sage: G.<a,b> = AbelianGroup(2)
sage: A = G.subgroup([a])
sage: A.gen(0)
a
Return True if  is an abelian group.
is an abelian group.
EXAMPLES:
sage: from sage.groups.abelian_gps.abelian_group import is_AbelianGroup
sage: F = AbelianGroup(5,[5,5,7,8,9],names = list("abcde")); F
Multiplicative Abelian Group isomorphic to C5 x C5 x C7 x C8 x C9
sage: is_AbelianGroup(F)
True
sage: is_AbelianGroup(AbelianGroup(7, [3]*7))
True
G and H are abelian, g in G, H is a subgroup of G generated by a list (words) of elements of G. If g is in H, return the expression for g as a word in the elements of (words).
The ‘word problem’ for a finite abelian group G boils down to the following matrix-vector analog of the Chinese remainder theorem.
Problem: Fix integers 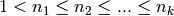 (indeed, these
(indeed, these 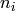 will all be prime powers), fix a
generating set
will all be prime powers), fix a
generating set 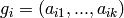 (with
(with
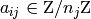 ), for
), for 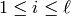 ,
for the group
,
for the group 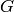 , and let
, and let 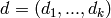 be
an element of the direct product
be
an element of the direct product
 . Find, if they
exist, integers
. Find, if they
exist, integers 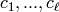 such that
such that
 . In other words, solve
the equation
. In other words, solve
the equation 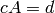 for
for 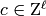 , where
, where
 is the matrix whose rows are the
is the matrix whose rows are the 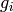 ‘s. Of
course, it suffices to restrict the
‘s. Of
course, it suffices to restrict the 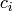 ‘s to the range
‘s to the range
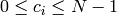 , where
, where  denotes the least
common multiple of the integers
denotes the least
common multiple of the integers 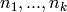 .
.
This function does not solve this directly, as perhaps it should. Rather (for both speed and as a model for a similar function valid for more general groups), it pushes it over to GAP, which has optimized (non-deterministic) algorithms for the word problem. Essentially, this function is a wrapper for the GAP function ‘Factorization’.
EXAMPLE:
sage: G.<a,b,c> = AbelianGroup(3,[2,3,4]); G
Multiplicative Abelian Group isomorphic to C2 x C3 x C4
sage: w = word_problem([a*b,a*c], b*c); w #random
[[a*b, 1], [a*c, 1]]
sage: prod([x^i for x,i in w]) == b*c
True
sage: w = word_problem([a*c,c],a); w #random
[[a*c, 1], [c, -1]]
sage: prod([x^i for x,i in w]) == a
True
sage: word_problem([a*c,c],a,verbose=True) #random
a = (a*c)^1*(c)^-1
[[a*c, 1], [c, -1]]
sage: A.<a,b,c,d,e> = AbelianGroup(5,[4, 5, 5, 7, 8])
sage: b1 = a^3*b*c*d^2*e^5
sage: b2 = a^2*b*c^2*d^3*e^3
sage: b3 = a^7*b^3*c^5*d^4*e^4
sage: b4 = a^3*b^2*c^2*d^3*e^5
sage: b5 = a^2*b^4*c^2*d^4*e^5
sage: w = word_problem([b1,b2,b3,b4,b5],e); w #random
[[a^3*b*c*d^2*e^5, 1], [a^2*b*c^2*d^3*e^3, 1], [a^3*b^3*d^4*e^4, 3], [a^2*b^4*c^2*d^4*e^5, 1]]
sage: prod([x^i for x,i in w]) == e
True
sage: word_problem([a,b,c,d,e],e)
[[e, 1]]
sage: word_problem([a,b,c,d,e],b)
[[b, 1]]
Warning