AUTHORS:
We test that pickling works:
sage: K.<a> = NumberField(x^2 - 5)
sage: I = K.ideal(2/(5+a))
sage: I == loads(dumps(I))
True
Bases: sage.rings.number_field.number_field_ideal.NumberFieldIdeal
A fractional ideal in a number field.
Return the denominator ideal of this fractional ideal. Each
fractional ideal has a unique expression as 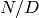 where
where  ,
,
 are coprime integral ideals; the denominator is
are coprime integral ideals; the denominator is  .
.
EXAMPLES:
sage: K.<i>=NumberField(x^2+1)
sage: I = K.ideal((3+4*i)/5); I
Fractional ideal (4/5*i + 3/5)
sage: I.denominator()
Fractional ideal (2*i + 1)
sage: I.numerator()
Fractional ideal (-i - 2)
sage: I.numerator().is_integral() and I.denominator().is_integral()
True
sage: I.numerator() + I.denominator() == K.unit_ideal()
True
sage: I.numerator()/I.denominator() == I
True
Returns True if this ideal divides other and False otherwise.
EXAMPLES:
sage: K.<a> = CyclotomicField(11); K
Cyclotomic Field of order 11 and degree 10
sage: I = K.factor(31)[0][0]; I
Fractional ideal (-3*a^7 - 4*a^5 - 3*a^4 - 3*a^2 - 3*a - 3)
sage: I.divides(I)
True
sage: I.divides(31)
True
sage: I.divides(29)
False
Returns an element  in this ideal such that
in this ideal such that 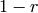 is in other
is in other
An error is raised if either ideal is not integral of if they are not coprime.
INPUT:
OUTPUT:
An element  of the ideal self such that
of the ideal self such that 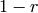 is in the ideal other
is in the ideal other
AUTHOR: Maite Aranes (modified to use PARI’s idealaddtoone by Francis Clarke)
EXAMPLES:
sage: K.<a> = NumberField(x^3-2)
sage: A = K.ideal(a+1); A; A.norm()
Fractional ideal (a + 1)
3
sage: B = K.ideal(a^2-4*a+2); B; B.norm()
Fractional ideal (a^2 - 4*a + 2)
68
sage: r = A.element_1_mod(B); r
a^2 + 5
sage: r in A
True
sage: 1-r in B
True
TESTS:
sage: K.<a> = NumberField(x^3-2)
sage: A = K.ideal(a+1)
sage: B = K.ideal(a^2-4*a+1); B; B.norm()
Fractional ideal (a^2 - 4*a + 1)
99
sage: A.element_1_mod(B)
...
TypeError: Fractional ideal (a + 1), Fractional ideal (a^2 - 4*a + 1) are not coprime ideals
sage: B = K.ideal(1/a); B
Fractional ideal (1/2*a^2)
sage: A.element_1_mod(B)
...
TypeError: Fractional ideal (1/2*a^2) is not an integral ideal
Returns the Euler 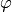 -function of this integral ideal.
-function of this integral ideal.
This is the order of the multiplicative group of the quotient modulo the ideal.
An error is raised if the ideal is not integral.
EXAMPLES:
sage: K.<i>=NumberField(x^2+1)
sage: I = K.ideal(2+i)
sage: [r for r in I.residues() if I.is_coprime(r)]
[-2*i, -i, i, 2*i]
sage: I.euler_phi()
4
sage: J = I^3
sage: J.euler_phi()
100
sage: len([r for r in J.residues() if J.is_coprime(r)])
100
sage: J = K.ideal(3-2*i)
sage: I.is_coprime(J)
True
sage: I.euler_phi()*J.euler_phi() == (I*J).euler_phi()
True
sage: L.<b> = K.extension(x^2 - 7)
sage: L.ideal(3).euler_phi()
64
Factorization of this ideal in terms of prime ideals.
EXAMPLES:
sage: K.<a> = NumberField(x^4 + 23); K
Number Field in a with defining polynomial x^4 + 23
sage: I = K.ideal(19); I
Fractional ideal (19)
sage: F = I.factor(); F
(Fractional ideal (a^2 + 2*a + 2)) * (Fractional ideal (a^2 - 2*a + 2))
sage: type(F)
<class 'sage.structure.factorization.Factorization'>
sage: list(F)
[(Fractional ideal (a^2 + 2*a + 2), 1), (Fractional ideal (a^2 - 2*a + 2), 1)]
sage: F.prod()
Fractional ideal (19)
Returns l such that l*self is coprime to J.
INPUT:
OUTPUT:
TODO: Extend the implementation to non-integral ideals.
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 23)
sage: A = k.ideal(a+1)
sage: B = k.ideal(3)
sage: A.is_coprime(B)
False
sage: lam = A.idealcoprime(B); lam
-1/6*a + 1/6
sage: (lam*A).is_coprime(B)
True
ALGORITHM: Uses Pari function idealcoprime.
Returns the discrete logarithm of x with respect to the generators given in the bid structure of the ideal self.
INPUT:
OUTPUT:
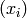 such that
such that 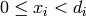 and
and
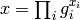 in
in 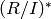 , where
, where  = self,
= self,  = ring of
integers of the field, and
= ring of
integers of the field, and 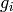 are the generators of
are the generators of 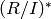 , of
orders
, of
orders 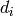 respectively, as given in the bid structure of
the ideal self.
respectively, as given in the bid structure of
the ideal self.EXAMPLES:
sage: k.<a> = NumberField(x^3 - 11)
sage: A = k.ideal(5)
sage: G = A.idealstar(2)
sage: l = A.ideallog(a^2 +3)
sage: r = prod([G.gens()[i]**l[i] for i in range(len(l))])
sage: (a^2 + 3) - r in A
True
sage: A.small_residue(r) # random
a^2 - 2
ALGORITHM: Uses Pari function ideallog
Returns the finite abelian group 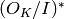 , where I is the ideal self
of the number field K, and
, where I is the ideal self
of the number field K, and 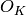 is the ring of integers of K.
is the ring of integers of K.
INPUT:
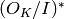 , which
takes more time. By default flag =1 (no generators are
computed). In both cases the special pari structure bid
is computed as well. If flag =0 (deprecated) it computes
only the group structure of
, which
takes more time. By default flag =1 (no generators are
computed). In both cases the special pari structure bid
is computed as well. If flag =0 (deprecated) it computes
only the group structure of 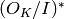 (with generators)
and not the special bid structure.
(with generators)
and not the special bid structure.OUTPUT:
The finite abelian group 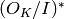 .
.
Note
Uses the pari function idealstar. The pari function outputs a special bid structure which is stored in the internal field _bid of the ideal (when flag=1,2). The special structure bid is used in the pari function ideallog to compute discrete logarithms.
EXAMPLES:
sage: k.<a> = NumberField(x^3 - 11)
sage: A = k.ideal(5)
sage: G = A.idealstar(); G
Multiplicative Abelian Group isomorphic to C24 x C4
sage: G.gens()
(f0, f1)
sage: G = A.idealstar(2)
sage: all([G.gens()[i] in k for i in range(G.ngens())])
True
ALGORITHM: Uses Pari function idealstar
Returns a iterator through a list of invertible residues modulo this integral ideal.
An error is raised if this fractional ideal is not integral.
INPUT:
OUTPUT:
 , i.e. a list of elements in the ring of integers
, i.e. a list of elements in the ring of integers  representing
the elements of
representing
the elements of 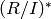 .
.ALGORITHM: Use pari’s idealstar to find the group structure and generators of the multiplicative group modulo the ideal.
EXAMPLES:
sage: K.<i>=NumberField(x^2+1)
sage: ires = K.ideal(2).invertible_residues(); ires # random address
<generator object at 0xa2feb6c>
sage: list(ires)
[-1, -i]
sage: list(K.ideal(2+i).invertible_residues())
[1, 2, -1, -2]
sage: list(K.ideal(i).residues())
[0]
sage: list(K.ideal(i).invertible_residues())
[1]
sage: I = K.ideal(3+6*i)
sage: units=I.invertible_residues()
sage: len(list(units))==I.euler_phi()
True
sage: K.<a> = NumberField(x^3-10)
sage: I = K.ideal(a-1)
sage: len(list(I.invertible_residues())) == I.euler_phi()
True
sage: K.<z> = CyclotomicField(10)
sage: len(list(K.primes_above(3)[0].invertible_residues()))
80
AUTHOR: John Cremona
Returns a iterator through a list of representatives for the invertible residues modulo this integral ideal, modulo the subgroup generated by the elements in the list subgp_gens.
INPUT:
Note
See also invertible_residues() for a simpler version without the subgroup.
OUTPUT:
 representing the elements of
representing the elements of 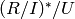 , where
, where  is this ideal and
is this ideal and
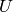 is the subgroup of
is the subgroup of 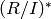 generated by subgp_gens.
generated by subgp_gens.EXAMPLES:
sage: k.<a> = NumberField(x^2 +23)
sage: I = k.ideal(a)
sage: list(I.invertible_residues_mod([-1]))
[1, 5, 2, 10, 4, -3, 8, -6, -7, 11, 9]
sage: list(I.invertible_residues_mod([1/2]))
[1, 5]
sage: list(I.invertible_residues_mod([23]))
...
TypeError: the element must be invertible mod the ideal
sage: K.<a> = NumberField(x^3-10)
sage: I = K.ideal(a-1)
sage: len(list(I.invertible_residues_mod([]))) == I.euler_phi()
True
sage: I = K.ideal(1)
sage: list(I.invertible_residues_mod([]))
[1]
sage: K.<z> = CyclotomicField(10)
sage: len(list(K.primes_above(3)[0].invertible_residues_mod([])))
80
AUTHOR: Maite Aranes.
Returns True if this ideal is coprime to the other, else False.
INPUT:
OUTPUT:
True if self and other are coprime, else False.
Note
This function works for fractional ideals as well as integral ideals.
AUTHOR: John Cremona
EXAMPLES:
sage: K.<i>=NumberField(x^2+1)
sage: I = K.ideal(2+i)
sage: J = K.ideal(2-i)
sage: I.is_coprime(J)
True
sage: (I^-1).is_coprime(J^3)
True
sage: I.is_coprime(5)
False
sage: I.is_coprime(6+i)
True
# See trac \# 4536:
sage: E.<a> = NumberField(x^5 + 7*x^4 + 18*x^2 + x - 3)
sage: OE = E.ring_of_integers()
sage: i,j,k = [u[0] for u in factor(3*OE)]
sage: (i/j).is_coprime(j/k)
False
sage: (j/k).is_coprime(j/k)
False
sage: F.<a, b> = NumberField([x^2 - 2, x^2 - 3])
sage: F.ideal(3 - a*b).is_coprime(F.ideal(3))
False
Return True if this ideal is maximal. This is equivalent to self being prime, since it is nonzero.
EXAMPLES:
sage: K.<a> = NumberField(x^3 + 3); K
Number Field in a with defining polynomial x^3 + 3
sage: K.ideal(5).is_maximal()
False
sage: K.ideal(7).is_maximal()
True
Returns True if this is a trivial ideal.
EXAMPLES:
sage: F.<a> = QuadraticField(-5)
sage: I = F.ideal(3)
sage: I.is_trivial()
False
sage: J = F.ideal(5)
sage: J.is_trivial()
False
sage: (I+J).is_trivial()
True
Return the numerator ideal of this fractional ideal.
Each fractional ideal has a unique expression as 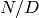 where
where  ,
,
 are coprime integral ideals. The numerator is
are coprime integral ideals. The numerator is  .
.
EXAMPLES:
sage: K.<i>=NumberField(x^2+1)
sage: I = K.ideal((3+4*i)/5); I
Fractional ideal (4/5*i + 3/5)
sage: I.denominator()
Fractional ideal (2*i + 1)
sage: I.numerator()
Fractional ideal (-i - 2)
sage: I.numerator().is_integral() and I.denominator().is_integral()
True
sage: I.numerator() + I.denominator() == K.unit_ideal()
True
sage: I.numerator()/I.denominator() == I
True
Return a list of the prime ideal factors of self
EXAMPLES:
sage: K.<w> = NumberField(x^2 + 23)
sage: I = ideal(w+1)
sage: I.prime_factors()
[Fractional ideal (2, 1/2*w - 1/2),
Fractional ideal (2, 1/2*w + 1/2),
Fractional ideal (3, -1/2*w - 1/2)]
Version for integral ideals of the prime_to_m_part function over  .
Returns the largest divisor of self that is coprime to the ideal M.
.
Returns the largest divisor of self that is coprime to the ideal M.
INPUT:
OUTPUT:
An ideal which is the largest divisor of self that is coprime to  .
.
AUTHOR: Maite Aranes
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 23)
sage: I = k.ideal(a+1)
sage: M = k.ideal(2, 1/2*a - 1/2)
sage: J = I.prime_to_idealM_part(M); J
Fractional ideal (12, 1/2*a + 13/2)
sage: J.is_coprime(M)
True
sage: J = I.prime_to_idealM_part(2); J
Fractional ideal (3, -1/2*a - 1/2)
sage: J.is_coprime(M)
True
Return the ramification index of this fractional ideal, assuming it is prime. Otherwise, raise a ValueError.
The ramification index is the power of this prime appearing in
the factorization of the prime in  that this prime lies
over.
that this prime lies
over.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 2); K
Number Field in a with defining polynomial x^2 + 2
sage: f = K.factor(2); f
(Fractional ideal (-a))^2
sage: f[0][0].ramification_index()
2
sage: K.ideal(13).ramification_index()
1
sage: K.ideal(17).ramification_index()
...
ValueError: the fractional ideal (= Fractional ideal (17)) is not prime
Return the canonical reduction of the element of  modulo the ideal
modulo the ideal
 (=self). This is an element of
(=self). This is an element of  (the ring of integers of the
number field) that is equivalent modulo
(the ring of integers of the
number field) that is equivalent modulo  to
to  .
.
An error is raised if this fractional ideal is not integral or
the element  is not integral.
is not integral.
INPUT:
OUTPUT:
An integral element 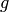 , such that
, such that 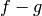 belongs to the ideal self
and such that
belongs to the ideal self
and such that 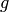 is a canonical reduced representative of the coset
is a canonical reduced representative of the coset
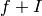 (
( =self) as described in the residues function, namely an integral element with coordinates
=self) as described in the residues function, namely an integral element with coordinates 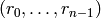 , where:
, where:
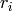 is reduced modulo
is reduced modulo 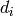
![d_i = b_i[i]](../../../_images/math/84299464cf18ad12e79eff85bb417450b459c3ce.png) , with
, with 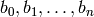 HNF basis
of the ideal self.
HNF basis
of the ideal self.Note
The reduced element 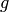 is not necessarily small. To get a
small
is not necessarily small. To get a
small 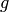 use the method small_residue.
use the method small_residue.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + 11)
sage: I = k.ideal(5, a^2 - a + 1)
sage: c = 4*a + 9
sage: I.reduce(c)
a^2 - 2*a
sage: c - I.reduce(c) in I
True
The reduced element is in the list of canonical representatives returned by the residues method:
sage: I.reduce(c) in list(I.residues())
True
The reduced element does not necessarily have smaller norm (use small_residue for that)
sage: c.norm()
25
sage: (I.reduce(c)).norm()
209
sage: (I.small_residue(c)).norm()
10
Sometimes the canonical reduced representative of  won’t be
won’t be  (it depends on the choice of basis for the ring of integers):
(it depends on the choice of basis for the ring of integers):
sage: k.<a> = NumberField(x^2 + 23)
sage: I = k.ideal(3)
sage: I.reduce(3*a + 1)
-3/2*a - 1/2
sage: k.ring_of_integers().basis()
[1/2*a + 1/2, a]
AUTHOR: Maite Aranes.
Return the residue class degree of this fractional ideal, assuming it is prime. Otherwise, raise a ValueError.
The residue class degree of a prime ideal  is the degree of
the extension
is the degree of
the extension 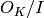 of its prime subfield.
of its prime subfield.
EXAMPLES:
sage: K.<a> = NumberField(x^5 + 2); K
Number Field in a with defining polynomial x^5 + 2
sage: f = K.factor(19); f
(Fractional ideal (a^2 + a - 3)) * (Fractional ideal (-2*a^4 - a^2 + 2*a - 1)) * (Fractional ideal (a^2 + a - 1))
sage: [i.residue_class_degree() for i, _ in f]
[2, 2, 1]
Return the residue class field of this fractional ideal, which must be prime.
EXAMPLES:
sage: K.<a> = NumberField(x^3-7)
sage: P = K.ideal(29).factor()[0][0]
sage: P.residue_field()
Residue field in abar of Fractional ideal (2*a^2 + 3*a - 10)
sage: P.residue_field('z')
Residue field in z of Fractional ideal (2*a^2 + 3*a - 10)
Another example:
sage: K.<a> = NumberField(x^3-7)
sage: P = K.ideal(389).factor()[0][0]; P
Fractional ideal (389, a^2 - 44*a - 9)
sage: P.residue_class_degree()
2
sage: P.residue_field()
Residue field in abar of Fractional ideal (389, a^2 - 44*a - 9)
sage: P.residue_field('z')
Residue field in z of Fractional ideal (389, a^2 - 44*a - 9)
sage: FF.<w> = P.residue_field()
sage: FF
Residue field in w of Fractional ideal (389, a^2 - 44*a - 9)
sage: FF((a+1)^390)
36
sage: FF(a)
w
An example of reduction maps to the residue field: these are defined on the whole valuation ring, i.e. the subring of the number field consisting of elements with non-negative valuation. This shows that the issue raised in trac #1951 has been fixed:
sage: K.<i> = NumberField(x^2 + 1)
sage: P1, P2 = [g[0] for g in K.factor(5)]; (P1,P2)
(Fractional ideal (-i - 2), Fractional ideal (2*i + 1))
sage: a = 1/(1+2*i)
sage: F1, F2 = [g.residue_field() for g in [P1,P2]]; (F1,F2)
(Residue field of Fractional ideal (-i - 2),
Residue field of Fractional ideal (2*i + 1))
sage: a.valuation(P1)
0
sage: F1(i/7)
4
sage: F1(a)
3
sage: a.valuation(P2)
-1
sage: F2(a)
Traceback (most recent call last):
ZeroDivisionError: Cannot reduce field element -2/5*i + 1/5 modulo Fractional ideal (2*i + 1): it has negative valuation
An example with a relative number field:
sage: L.<a,b> = NumberField([x^2 + 1, x^2 - 5])
sage: p = L.ideal((-1/2*b - 1/2)*a + 1/2*b - 1/2)
sage: R = p.residue_field(); R
Residue field in abar of Fractional ideal ((-1/2*b - 1/2)*a + 1/2*b - 1/2)
sage: R.cardinality()
9
sage: R(17)
2
sage: R((a + b)/17)
abar
sage: R(1/b)
2*abar
Returns a iterator through a complete list of residues modulo this integral ideal.
An error is raised if this fractional ideal is not integral.
OUTPUT:
An iterator through a complete list of residues modulo the integral
ideal self. This list is the set of canonical reduced representatives
given by all integral elements with coordinates 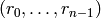 ,
where:
,
where:
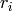 is reduced modulo
is reduced modulo 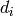
![d_i = b_i[i]](../../../_images/math/84299464cf18ad12e79eff85bb417450b459c3ce.png) , with
, with 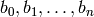 HNF basis
of the ideal.
HNF basis
of the ideal.AUTHOR: John Cremona (modified by Maite Aranes)
EXAMPLES:
sage: K.<i>=NumberField(x^2+1)
sage: res = K.ideal(2).residues(); res # random address
xmrange_iter([[0, 1], [0, 1]], <function <lambda> at 0xa252144>)
sage: list(res)
[0, i, 1, i + 1]
sage: list(K.ideal(2+i).residues())
[-2*i, -i, 0, i, 2*i]
sage: list(K.ideal(i).residues())
[0]
sage: I = K.ideal(3+6*i)
sage: reps=I.residues()
sage: len(list(reps)) == I.norm()
True
sage: all([r==s or not (r-s) in I for r in reps for s in reps])
True
sage: K.<a> = NumberField(x^3-10)
sage: I = K.ideal(a-1)
sage: len(list(I.residues())) == I.norm()
True
sage: K.<z> = CyclotomicField(11)
sage: len(list(K.primes_above(3)[0].residues())) == 3**5
True
Given an element  of the ambient number field, returns an
element
of the ambient number field, returns an
element 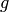 such that
such that 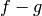 belongs to the ideal self (which
must be integral), and
belongs to the ideal self (which
must be integral), and 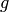 is small.
is small.
Note
The reduced representative returned is not uniquely determined.
ALGORITHM: Uses Pari function nfeltreduce.
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 5)
sage: I = k.ideal(a)
sage: I.small_residue(14)
-1
sage: K.<a> = NumberField(x^5 + 7*x^4 + 18*x^2 + x - 3)
sage: I = K.ideal(5)
sage: I.small_residue(a^2 -13)
a^2 + 5*a - 3
Bases: sage.rings.ideal.Ideal_generic
An ideal of a number field.
A synonym for norm.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.ideal(1 + 2*i).absolute_norm()
5
A synonym for ramification_index.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.ideal(1 + i).absolute_ramification_index()
2
Return the Artin symbol 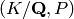 , where
, where  is the
number field of
is the
number field of  =self. This is the unique element
=self. This is the unique element  of
the decomposition group of
of
the decomposition group of  such that
such that 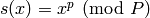 where
where  is the residue characteristic of
is the residue characteristic of  . (Here
. (Here  (self) should be prime and unramified.)
(self) should be prime and unramified.)
See the artin_symbol method of the GaloisGroup_v2 class for further documentation and examples.
EXAMPLE:
sage: QuadraticField(-23, 'w').primes_above(7)[0].artin_symbol()
(1,2)
Return an immutable sequence of elements of this ideal (note:
their parent is the number field) that form a basis for this
ideal viewed as a  -module.
-module.
EXAMPLES:
sage: K.<z> = CyclotomicField(7)
sage: I = K.factor(11)[0][0]
sage: I.basis() # warning -- choice of basis can be somewhat random
[11, 11*z, 11*z^2, z^3 + 5*z^2 + 4*z + 10, z^4 + z^2 + z + 5, z^5 + z^4 + z^3 + 2*z^2 + 6*z + 5]
An example of a non-integral ideal.:
sage: J = 1/I
sage: J # warning -- choice of generators can be somewhat random
Fractional ideal (2/11*z^5 + 2/11*z^4 + 3/11*z^3 + 2/11)
sage: J.basis() # warning -- choice of basis can be somewhat random
[1, z, z^2, 1/11*z^3 + 7/11*z^2 + 6/11*z + 10/11, 1/11*z^4 + 1/11*z^2 + 1/11*z + 7/11, 1/11*z^5 + 1/11*z^4 + 1/11*z^3 + 2/11*z^2 + 8/11*z + 7/11]
Returns the coordinate vector of  with respect to this ideal.
with respect to this ideal.
 (the degree of the field) giving
the coordinates of
(the degree of the field) giving
the coordinates of  with respect to the integral basis
of the ideal. In general this will be a vector of
rationals; it will consist of integers if and only if
with respect to the integral basis
of the ideal. In general this will be a vector of
rationals; it will consist of integers if and only if  is in the ideal.
is in the ideal.AUTHOR: John Cremona 2008-10-31
ALGORITHM:
Uses linear algebra. The change-of-basis matrix is cached. Provides simpler implementations for _contains_(), is_integral() and smallest_integer().
EXAMPLES:
sage: K.<i> = QuadraticField(-1)
sage: I = K.ideal(7+3*i)
sage: Ibasis = I.integral_basis(); Ibasis
[58, i + 41]
sage: a = 23-14*i
sage: acoords = I.coordinates(a); acoords
(597/58, -14)
sage: sum([Ibasis[j]*acoords[j] for j in range(2)]) == a
True
sage: b = 123+456*i
sage: bcoords = I.coordinates(b); bcoords
(-18573/58, 456)
sage: sum([Ibasis[j]*bcoords[j] for j in range(2)]) == b
True
Return the decomposition group of self, as a subset of the automorphism group of the number field of self. Raises an error if the field isn’t Galois. See the decomposition_group method of the GaloisGroup_v2 class for further examples and doctests.
EXAMPLE:
sage: QuadraticField(-23, 'w').primes_above(7)[0].decomposition_group()
Galois group of Number Field in w with defining polynomial x^2 + 23
Return the free  -module contained in the vector space
associated to the ambient number field, that corresponds
to this ideal.
-module contained in the vector space
associated to the ambient number field, that corresponds
to this ideal.
EXAMPLES:
sage: K.<z> = CyclotomicField(7)
sage: I = K.factor(11)[0][0]; I
Fractional ideal (-2*z^4 - 2*z^2 - 2*z + 1)
sage: A = I.free_module()
sage: A # warning -- choice of basis can be somewhat random
Free module of degree 6 and rank 6 over Integer Ring
User basis matrix:
[11 0 0 0 0 0]
[ 0 11 0 0 0 0]
[ 0 0 11 0 0 0]
[10 4 5 1 0 0]
[ 5 1 1 0 1 0]
[ 5 6 2 1 1 1]
However, the actual  -module is not at all random:
-module is not at all random:
sage: A.basis_matrix().change_ring(ZZ).echelon_form()
[ 1 0 0 5 1 1]
[ 0 1 0 1 1 7]
[ 0 0 1 7 6 10]
[ 0 0 0 11 0 0]
[ 0 0 0 0 11 0]
[ 0 0 0 0 0 11]
The ideal doesn’t have to be integral:
sage: J = I^(-1)
sage: B = J.free_module()
sage: B.echelonized_basis_matrix()
[ 1/11 0 0 7/11 1/11 1/11]
[ 0 1/11 0 1/11 1/11 5/11]
[ 0 0 1/11 5/11 4/11 10/11]
[ 0 0 0 1 0 0]
[ 0 0 0 0 1 0]
[ 0 0 0 0 0 1]
This also works for relative extensions:
sage: K.<a,b> = NumberField([x^2 + 1, x^2 + 2])
sage: I = K.fractional_ideal(4)
sage: I.free_module()
Free module of degree 4 and rank 4 over Integer Ring
User basis matrix:
[ 4 0 0 0]
[ -3 7 -1 1]
[ 3 7 1 1]
[ 0 -10 0 -2]
sage: J = I^(-1); J.free_module()
Free module of degree 4 and rank 4 over Integer Ring
User basis matrix:
[ 1/4 0 0 0]
[-3/16 7/16 -1/16 1/16]
[ 3/16 7/16 1/16 1/16]
[ 0 -5/8 0 -1/8]
An example of intersecting ideals by intersecting free modules.:
sage: K.<a> = NumberField(x^3 + x^2 - 2*x + 8)
sage: I = K.factor(2)
sage: p1 = I[0][0]; p2 = I[1][0]
sage: N = p1.free_module().intersection(p2.free_module()); N
Free module of degree 3 and rank 3 over Integer Ring
Echelon basis matrix:
[ 1 1/2 1/2]
[ 0 1 1]
[ 0 0 2]
sage: N.index_in(p1.free_module()).abs()
2
TESTS:
Sage can find the free module associated to quite large ideals quickly (see trac #4627):
sage: y = polygen(ZZ)
sage: M.<a> = NumberField(y^20 - 2*y^19 + 10*y^17 - 15*y^16 + 40*y^14 - 64*y^13 + 46*y^12 + 8*y^11 - 32*y^10 + 8*y^9 + 46*y^8 - 64*y^7 + 40*y^6 - 15*y^4 + 10*y^3 - 2*y + 1)
sage: M.ideal(prod(prime_range(6000, 6200))).free_module()
Free module of degree 20 and rank 20 over Integer Ring
User basis matrix:
20 x 20 dense matrix over Rational Field
Express this ideal in terms of at most two generators, and one if possible.
Note that if the ideal is not principal, then this uses PARI’s idealtwoelt function, which takes exponential time, the first time it is called for each ideal. Also, this indirectly uses bnfisprincipal, so set proof=True if you want to prove correctness (which is the default).
EXAMPLES:
sage: R.<x> = PolynomialRing(QQ)
sage: K.<i> = NumberField(x^2+1, 'i')
sage: J = K.ideal([i+1, 2])
sage: J.gens()
(i + 1, 2)
sage: J.gens_reduced()
(i + 1,)
TESTS:
sage: all(j.parent() is K for j in J.gens())
True
sage: all(j.parent() is K for j in J.gens_reduced())
True
sage: K.<a> = NumberField(x^4 + 10*x^2 + 20)
sage: J = K.prime_above(5)
sage: J.is_principal()
False
sage: J.gens_reduced()
(5, a)
sage: all(j.parent() is K for j in J.gens())
True
sage: all(j.parent() is K for j in J.gens_reduced())
True
Return the inertia group of self, i.e. the set of elements s of the Galois group of the number field of self (which we assume is Galois) such that s acts trivially modulo self. This is the same as the 0th ramification group of self. See the inertia_group method of the GaloisGroup_v2 class for further examples and doctests.
EXAMPLE:
sage: QuadraticField(-23, 'w').primes_above(23)[0].inertia_group()
Galois group of Number Field in w with defining polynomial x^2 + 23
Return a list of generators for this ideal as a  -module.
-module.
EXAMPLES:
sage: R.<x> = PolynomialRing(QQ)
sage: K.<i> = NumberField(x^2 + 1)
sage: J = K.ideal(i+1)
sage: J.integral_basis()
[2, i + 1]
Return a tuple 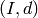 , where
, where  is an integral ideal, and
is an integral ideal, and  is the
smallest positive integer such that this ideal is equal to
is the
smallest positive integer such that this ideal is equal to 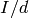 .
.
EXAMPLES:
sage: R.<x> = PolynomialRing(QQ)
sage: K.<a> = NumberField(x^2-5)
sage: I = K.ideal(2/(5+a))
sage: I.is_integral()
False
sage: J,d = I.integral_split()
sage: J
Fractional ideal (-1/2*a + 5/2)
sage: J.is_integral()
True
sage: d
5
sage: I == J/d
True
Return the intersection of self and other.
EXAMPLE:
sage: K.<a> = QuadraticField(-11)
sage: p = K.ideal((a + 1)/2); q = K.ideal((a + 3)/2)
sage: p.intersection(q) == q.intersection(p) == K.ideal(a-2)
True
An example with non-principal ideals:
sage: L.<a> = NumberField(x^3 - 7)
sage: p = L.ideal(a^2 + a + 1, 2)
sage: q = L.ideal(a+1)
sage: p.intersection(q) == L.ideal(8, 2*a + 2)
True
A relative example:
sage: L.<a,b> = NumberField([x^2 + 11, x^2 - 5])
sage: A = L.ideal([15, (-3/2*b + 7/2)*a - 8])
sage: B = L.ideal([6, (-1/2*b + 1)*a - b - 5/2])
sage: A.intersection(B) == L.ideal(-1/2*a - 3/2*b - 1)
True
Return True if this ideal is integral.
EXAMPLES:
sage: R.<x> = PolynomialRing(QQ)
sage: K.<a> = NumberField(x^5-x+1)
sage: K.ideal(a).is_integral()
True
sage: (K.ideal(1) / (3*a+1)).is_integral()
False
Return True if this ideal is maximal. This is equivalent to self being prime and nonzero.
EXAMPLES:
sage: K.<a> = NumberField(x^3 + 3); K
Number Field in a with defining polynomial x^3 + 3
sage: K.ideal(5).is_maximal()
False
sage: K.ideal(7).is_maximal()
True
Return True if this ideal is prime.
EXAMPLES:
sage: K.<a> = NumberField(x^2 - 17); K
Number Field in a with defining polynomial x^2 - 17
sage: K.ideal(5).is_prime()
True
sage: K.ideal(13).is_prime()
False
sage: K.ideal(17).is_prime()
False
Return True if this ideal is principal.
Since it uses the PARI method bnfisprincipal, specify proof=True (this is the default setting) to prove the correctness of the output.
EXAMPLES:
sage: K = QuadraticField(-119,’a’) sage: P = K.factor(2)[1][0] sage: P.is_principal() False sage: I = P^5 sage: I.is_principal() True sage: I # random Fractional ideal (-1/2*a + 3/2) sage: P = K.ideal([2]).factor()[1][0] sage: I = P^5 sage: I.is_principal() True
Return True iff self is the zero ideal
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 2); K
Number Field in a with defining polynomial x^2 + 2
sage: K.ideal(3).is_zero()
False
sage: I=K.ideal(0); I.is_zero()
True
sage: I
Ideal (0) of Number Field in a with defining polynomial x^2 + 2
(0 is a NumberFieldIdeal, not a NumberFieldFractionIdeal)
Return the norm of this fractional ideal as a rational number.
EXAMPLES:
sage: K.<a> = NumberField(x^4 + 23); K
Number Field in a with defining polynomial x^4 + 23
sage: I = K.ideal(19); I
Fractional ideal (19)
sage: factor(I.norm())
19^4
sage: F = I.factor()
sage: F[0][0].norm().factor()
19^2
Return the number field that this is a fractional ideal in.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 2); K
Number Field in a with defining polynomial x^2 + 2
sage: K.ideal(3).number_field()
Number Field in a with defining polynomial x^2 + 2
sage: K.ideal(0).number_field() # not tested (not implemented)
Number Field in a with defining polynomial x^2 + 2
Return PARI’s representation of this ideal in Hermite normal form.
EXAMPLES:
sage: R.<x> = PolynomialRing(QQ)
sage: K.<a> = NumberField(x^3 - 2)
sage: I = K.ideal(2/(5+a))
sage: I.pari_hnf()
[2, 0, 50/127; 0, 2, 244/127; 0, 0, 2/127]
Return the  ‘th ramification group of self, i.e. the set of
elements
‘th ramification group of self, i.e. the set of
elements  of the Galois group of the number field of self
(which we assume is Galois) such that
of the Galois group of the number field of self
(which we assume is Galois) such that  acts trivially
modulo the
acts trivially
modulo the 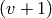 ‘st power of self. See the
ramification_group method of the GaloisGroup class for
further examples and doctests.
‘st power of self. See the
ramification_group method of the GaloisGroup class for
further examples and doctests.
EXAMPLE:
sage: QuadraticField(-23, 'w').primes_above(23)[0].ramification_group(0)
Galois group of Number Field in w with defining polynomial x^2 + 23
sage: QuadraticField(-23, 'w').primes_above(23)[0].ramification_group(1)
Subgroup [()] of Galois group of Number Field in w with defining polynomial x^2 + 23
Return a random element of this order.
INPUT:
OUTPUT:
A random element of this fractional ideal, computed as a random
 -linear combination of the basis.
-linear combination of the basis.
EXAMPLES:
sage: K.<a> = NumberField(x^3 + 2)
sage: I = K.ideal(1-a)
sage: I.random_element() # random output
-a^2 - a - 19
sage: I.random_element(distribution="uniform") # random output
a^2 - 2*a - 8
sage: I.random_element(-30,30) # random output
-7*a^2 - 17*a - 75
sage: I.random_element(-100, 200).is_integral()
True
sage: I.random_element(-30,30).parent() is K
True
A relative example:
sage: K.<a, b> = NumberField([x^2 + 2, x^2 + 1000*x + 1])
sage: I = K.ideal(1-a)
sage: I.random_element() # random output
17/500002*a^3 + 737253/250001*a^2 - 1494505893/500002*a + 752473260/250001
sage: I.random_element().is_integral()
True
sage: I.random_element(-100, 200).parent() is K
True
Return a small ideal that is equivalent to self in the group of fractional ideals modulo principal ideals. Very often (but not always) if self is principal then this function returns the unit ideal.
ALGORITHM: Calls pari’s idealred function.
EXAMPLES:
sage: K.<w> = NumberField(x^2 + 23)
sage: I = ideal(w*23^5); I
Fractional ideal (6436343*w)
sage: I.reduce_equiv()
Fractional ideal (1)
sage: I = K.class_group().0.ideal()^10; I
Fractional ideal (1024, 1/2*w + 979/2)
sage: I.reduce_equiv()
Fractional ideal (2, 1/2*w - 1/2)
A synonym for norm.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.ideal(1 + 2*i).relative_norm()
5
A synonym for ramification_index.
EXAMPLES:
sage: K.<i> = NumberField(x^2 + 1)
sage: K.ideal(1 + i).relative_ramification_index()
2
Return the smallest non-negative integer in 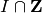 ,
where
,
where  is this ideal. If
is this ideal. If 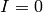 , returns 0.
, returns 0.
EXAMPLES:
sage: R.<x> = PolynomialRing(QQ)
sage: K.<a> = NumberField(x^2+6)
sage: I = K.ideal([4,a])/7
sage: I.smallest_integer()
2
sage: K.<i> = QuadraticField(-1)
sage: P1, P2 = [P for P,e in K.factor(13)]
sage: all([(P1^i*P2^j).smallest_integer() == 13^max(i,j,0) for i in range(-3,3) for j in range(-3,3)])
True
sage: I = K.ideal(0)
sage: I.smallest_integer()
0
# See trac\# 4392:
sage: K.<a>=QuadraticField(-5)
sage: I=K.ideal(7)
sage: I.smallest_integer()
7
sage: K.<z> = CyclotomicField(13)
sage: a = K([-8, -4, -4, -6, 3, -4, 8, 0, 7, 4, 1, 2])
sage: I = K.ideal(a)
sage: I.smallest_integer()
146196692151
sage: I.norm()
1315770229359
sage: I.norm() / I.smallest_integer()
9
Return the valuation of self at p.
INPUT:
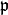 of this number field.
of this number field.OUTPUT:
(integer) The valuation of this fractional ideal at the prime
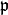 . If
. If 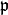 is not prime, raise a
ValueError.
is not prime, raise a
ValueError.
EXAMPLES:
sage: K.<a> = NumberField(x^5 + 2); K
Number Field in a with defining polynomial x^5 + 2
sage: i = K.ideal(38); i
Fractional ideal (38)
sage: i.valuation(K.factor(19)[0][0])
1
sage: i.valuation(K.factor(2)[0][0])
5
sage: i.valuation(K.factor(3)[0][0])
0
sage: i.valuation(0)
...
ValueError: p (= 0) must be nonzero
Given a basis  of elements for a
of elements for a  -submodule of a number
field
-submodule of a number
field  , return the corresponding
, return the corresponding  -submodule.
-submodule.
EXAMPLES:
sage: K.<w> = NumberField(x^4 + 1)
sage: from sage.rings.number_field.number_field_ideal import basis_to_module
sage: basis_to_module([K.0, K.0^2 + 3], K)
Free module of degree 4 and rank 2 over Integer Ring
User basis matrix:
[0 1 0 0]
[3 0 1 0]
Used internally in the number field ideal implementation for converting from the form output by the pari function idealprimedec to a Sage ideal.
INPUT:
EXAMPLE:
sage: from sage.rings.number_field.number_field_ideal import convert_from_idealprimedec_form
sage: K.<a> = NumberField(x^2 + 3)
sage: K_bnf = gp(K.pari_bnf())
sage: ideal = K_bnf.idealprimedec(3)[1]
sage: convert_from_idealprimedec_form(K, ideal)
Fractional ideal (1/2*a - 3/2)
sage: K.factor(3)
(Fractional ideal (1/2*a - 3/2))^2
Used internally in the number field ideal implementation for converting from the order basis to the number field basis.
INPUT:
EXAMPLES:
sage: from sage.rings.number_field.number_field_ideal import convert_from_zk_basis
sage: k.<a> = NumberField(x^2 + 23)
sage: I = k.factor(3)[0][0]; I
Fractional ideal (3, -1/2*a + 1/2)
sage: hnf = I.pari_hnf(); hnf
[3, 0; 0, 1]
sage: convert_from_zk_basis(k, hnf)
[3, 1/2*x - 1/2]
Used internally in the number field ideal implementation for converting to the form output by the pari function idealprimedec from a Sage ideal.
INPUT:
NOTE:
The algorithm implemented right now is not optimal, but works. It should eventually be replaced with something better.
EXAMPLE:
sage: from sage.rings.number_field.number_field_ideal import convert_to_idealprimedec_form
sage: K.<a> = NumberField(x^2 + 3)
sage: P = K.ideal(a/2-3/2)
sage: convert_to_idealprimedec_form(K, P)
[3, [1, 2]~, 2, 1, [1, -1]~]
Return True if x is a fractional ideal of a number field.
EXAMPLES:
sage: from sage.rings.number_field.number_field_ideal import is_NumberFieldFractionalIdeal
sage: is_NumberFieldFractionalIdeal(2/3)
False
sage: is_NumberFieldFractionalIdeal(ideal(5))
False
sage: k.<a> = NumberField(x^2 + 2)
sage: I = k.ideal([a + 1]); I
Fractional ideal (a + 1)
sage: is_NumberFieldFractionalIdeal(I)
True
sage: Z = k.ideal(0); Z
Ideal (0) of Number Field in a with defining polynomial x^2 + 2
sage: is_NumberFieldFractionalIdeal(Z)
False
Return True if x is an ideal of a number field.
EXAMPLES:
sage: from sage.rings.number_field.number_field_ideal import is_NumberFieldIdeal
sage: is_NumberFieldIdeal(2/3)
False
sage: is_NumberFieldIdeal(ideal(5))
False
sage: k.<a> = NumberField(x^2 + 2)
sage: I = k.ideal([a + 1]); I
Fractional ideal (a + 1)
sage: is_NumberFieldIdeal(I)
True
sage: Z = k.ideal(0); Z
Ideal (0) of Number Field in a with defining polynomial x^2 + 2
sage: is_NumberFieldIdeal(Z)
True
Given an integral ideal  that contains a prime number
that contains a prime number  , compute
a vector space
, compute
a vector space 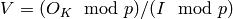 , along with a
homomorphism
, along with a
homomorphism 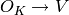 and a section
and a section 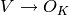 .
.
EXAMPLES:
sage: from sage.rings.number_field.number_field_ideal import quotient_char_p
sage: K.<i> = NumberField(x^2 + 1); O = K.maximal_order(); I = K.fractional_ideal(15)
sage: quotient_char_p(I, 5)[0]
Vector space quotient V/W of dimension 2 over Finite Field of size 5 where
V: Vector space of dimension 2 over Finite Field of size 5
W: Vector space of degree 2 and dimension 0 over Finite Field of size 5
Basis matrix:
[]
sage: quotient_char_p(I, 3)[0]
Vector space quotient V/W of dimension 2 over Finite Field of size 3 where
V: Vector space of dimension 2 over Finite Field of size 3
W: Vector space of degree 2 and dimension 0 over Finite Field of size 3
Basis matrix:
[]
sage: I = K.factor(13)[0][0]; I
Fractional ideal (-3*i - 2)
sage: I.residue_class_degree()
1
sage: quotient_char_p(I, 13)[0]
Vector space quotient V/W of dimension 1 over Finite Field of size 13 where
V: Vector space of dimension 2 over Finite Field of size 13
W: Vector space of degree 2 and dimension 1 over Finite Field of size 13
Basis matrix:
[1 8]