AUTHORS:
Bases: sage.structure.element.FieldElement
An element of a number field.
EXAMPLES:
sage: k.<a> = NumberField(x^3 + x + 1)
sage: a^3
-a - 1
Return the absolute value of this element with respect to the
 -th complex embedding of parent, to the given precision.
-th complex embedding of parent, to the given precision.
If prec is 53 (the default), then the complex double field is used; otherwise the arbitrary precision (but slow) complex field is used.
INPUT:
EXAMPLES:
sage: z = CyclotomicField(7).gen()
sage: abs(z)
1.00000000000000
sage: abs(z^2 + 17*z - 3)
16.0604426799931
sage: K.<a> = NumberField(x^3+17)
sage: abs(a)
2.57128159065824
sage: a.abs(prec=100)
2.5712815906582353554531872087
sage: a.abs(prec=100,i=1)
2.5712815906582353554531872087
sage: a.abs(100, 2)
2.5712815906582353554531872087
Here’s one where the absolute value depends on the embedding.
sage: K.<b> = NumberField(x^2-2)
sage: a = 1 + b
sage: a.abs(i=0)
0.414213562373095
sage: a.abs(i=1)
2.41421356237309
Return the non-archimedean absolute value of this element with
respect to the prime 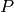 , to the given precision.
, to the given precision.
INPUT:
OUTPUT:
(real) the non-archimedean absolute value of this element with
respect to the prime 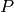 , to the given precision. This is the
normalised absolute value, so that the underlying prime number
, to the given precision. This is the
normalised absolute value, so that the underlying prime number
 has absolute value
has absolute value 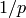 .
.
EXAMPLES:
sage: K.<a> = NumberField(x^2+5)
sage: [1/K(2).abs_non_arch(P) for P in K.primes_above(2)]
[2.00000000000000]
sage: [1/K(3).abs_non_arch(P) for P in K.primes_above(3)]
[3.00000000000000, 3.00000000000000]
sage: [1/K(5).abs_non_arch(P) for P in K.primes_above(5)]
[5.00000000000000]
A relative example:
sage: L.<b> = K.extension(x^2-5)
sage: [b.abs_non_arch(P) for P in L.primes_above(b)]
[0.447213595499958, 0.447213595499958]
Return the additive order of this element (i.e. infinity if self != 0, 1 if self == 0)
EXAMPLES:
sage: K.<u> = NumberField(x^4 - 3*x^2 + 3)
sage: u.additive_order()
+Infinity
sage: K(0).additive_order()
1
sage: K.ring_of_integers().characteristic() # implicit doctest
0
Return the i-th embedding of self in the complex numbers, to the given precision.
EXAMPLES:
sage: k.<a> = NumberField(x^3 - 2)
sage: a.complex_embedding()
-0.629960524947437 - 1.09112363597172*I
sage: a.complex_embedding(10)
-0.63 - 1.1*I
sage: a.complex_embedding(100)
-0.62996052494743658238360530364 - 1.0911236359717214035600726142*I
sage: a.complex_embedding(20, 1)
-0.62996 + 1.0911*I
sage: a.complex_embedding(20, 2)
1.2599
Return the images of this element in the floating point complex numbers, to the given bits of precision.
INPUT:
EXAMPLES:
sage: k.<a> = NumberField(x^3 - 2)
sage: a.complex_embeddings()
[-0.629960524947437 - 1.09112363597172*I, -0.629960524947437 + 1.09112363597172*I, 1.25992104989487]
sage: a.complex_embeddings(10)
[-0.63 - 1.1*I, -0.63 + 1.1*I, 1.3]
sage: a.complex_embeddings(100)
[-0.62996052494743658238360530364 - 1.0911236359717214035600726142*I, -0.62996052494743658238360530364 + 1.0911236359717214035600726142*I, 1.2599210498948731647672106073]
Return the complex conjugate of the number field element. Currently, this is implemented for cyclotomic fields and quadratic extensions of Q. It seems likely that there are other number fields for which the idea of a conjugate would be easy to compute.
EXAMPLES:
sage: k.<I> = QuadraticField(-1)
sage: I.conjugate()
-I
sage: (I/(1+I)).conjugate()
-1/2*I + 1/2
sage: z6=CyclotomicField(6).gen(0)
sage: (2*z6).conjugate()
-2*zeta6 + 2
sage: K.<j,b> = QQ[sqrt(-1), sqrt(2)]
sage: j.conjugate()
...
NotImplementedError: complex conjugation is not implemented (or doesn't make sense).
sage: K.<b> = NumberField(x^3 - 2)
sage: b.conjugate()
...
NotImplementedError: complex conjugation is not implemented (or doesn't make sense).
Let 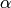 be self. Return a Python function that takes
any element of the parent of self in
be self. Return a Python function that takes
any element of the parent of self in  and writes it in terms of the powers of
and writes it in terms of the powers of 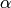 :
:
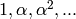 .
.
(NOT CACHED).
EXAMPLES:
This function allows us to write elements of a number field in terms of a different generator without having to construct a whole separate number field.
sage: y = polygen(QQ,'y'); K.<beta> = NumberField(y^3 - 2); K
Number Field in beta with defining polynomial y^3 - 2
sage: alpha = beta^2 + beta + 1
sage: c = alpha.coordinates_in_terms_of_powers(); c
Coordinate function that writes elements in terms of the powers of beta^2 + beta + 1
sage: c(beta)
[-2, -3, 1]
sage: c(alpha)
[0, 1, 0]
sage: c((1+beta)^5)
[3, 3, 3]
sage: c((1+beta)^10)
[54, 162, 189]
This function works even if self only generates a subfield of this number field.
sage: k.<a> = NumberField(x^6 - 5)
sage: alpha = a^3
sage: c = alpha.coordinates_in_terms_of_powers()
sage: c((2/3)*a^3 - 5/3)
[-5/3, 2/3]
sage: c
Coordinate function that writes elements in terms of the powers of a^3
sage: c(a)
...
ArithmeticError: vector is not in free module
Return the denominator of this element, which is by definition the denominator of the corresponding polynomial representation. I.e., elements of number fields are represented as a polynomial (in reduced form) modulo the modulus of the number field, and the denominator is the denominator of this polynomial.
EXAMPLES:
sage: K.<z> = CyclotomicField(3)
sage: a = 1/3 + (1/5)*z
sage: print a.denominator()
15
Return the denominator ideal of this number field element.
Note
A ValueError will be raised if this function is called on 0.
Note
See also numerator_ideal()
OUTPUT:
(integral ideal) The denominator ideal  of this element,
where for a non-zero number field element
of this element,
where for a non-zero number field element  , the principal
ideal generated by
, the principal
ideal generated by  has the form
has the form 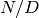 where
where  and
and  are coprime integral ideals. An error is raised if the
element is zero.
are coprime integral ideals. An error is raised if the
element is zero.
EXAMPLES:
sage: K.<a> = NumberField(x^2+5)
sage: b = (1+a)/2
sage: b.norm()
3/2
sage: D = b.denominator_ideal(); D
Fractional ideal (2, a + 1)
sage: D.norm()
2
sage: (1/b).denominator_ideal()
Fractional ideal (3, a + 1)
TESTS:
Undefined for 0:
sage: K(0).denominator_ideal()
...
ValueError: denominator ideal of 0 is not defined.
Return all Gal(Qbar/Q)-conjugates of this number field element in the field K.
EXAMPLES:
In the first example the conjugates are obvious:
sage: K.<a> = NumberField(x^2 - 2)
sage: a.galois_conjugates(K)
[a, -a]
sage: K(3).galois_conjugates(K)
[3]
In this example the field is not Galois, so we have to pass to an extension to obtain the Galois conjugates.
sage: K.<a> = NumberField(x^3 - 2)
sage: c = a.galois_conjugates(K); c
[a]
sage: K.<a> = NumberField(x^3 - 2)
sage: c = a.galois_conjugates(K.galois_closure('a1')); c
[1/84*a1^4 + 13/42*a1, -1/252*a1^4 - 55/126*a1, -1/126*a1^4 + 8/63*a1]
sage: c[0]^3
2
sage: parent(c[0])
Number Field in a1 with defining polynomial x^6 + 40*x^3 + 1372
sage: parent(c[0]).is_galois()
True
There is only one Galois conjugate of ![\sqrt[3]{2}](../../../_images/math/9fdfe572d1673f00f286d5ed753942d18f401cbb.png) in
in
![\QQ(\sqrt[3]{2})](../../../_images/math/c79d00be2051541ca454120136c786792a8bde88.png) .
.
sage: a.galois_conjugates(K)
[a]
Galois conjugates of ![\sqrt[3]{2}](../../../_images/math/9fdfe572d1673f00f286d5ed753942d18f401cbb.png) in the field
in the field
![\QQ(\zeta_3,\sqrt[3]{2})](../../../_images/math/6fdeb729748340a90437d95e4be2a31474d17ddd.png) :
:
sage: L.<a> = CyclotomicField(3).extension(x^3 - 2)
sage: a.galois_conjugates(L)
[a, (-zeta3 - 1)*a, zeta3*a]
Returns the absolute logarithmic height of this number field element.
INPUT:
OUTPUT:
(real) The absolute logarithmic height of this number field element; that is, the sum of the local heights at all finite and infinite places, with the contributions from the infinite places scaled by the degree to make the result independent of the parent field.
EXAMPLES:
sage: R.<x> = QQ[]
sage: K.<a> = NumberField(x^4+3*x^2-17)
sage: b = a/2
sage: b.global_height()
2.869222240687...
sage: b.global_height(prec=200)
2.8692222406879748488543678846959454765968722137813736080066
The global height of an algebraic number is absolute, i.e. it does not depend on th parent field:
sage: QQ(6).global_height()
1.79175946922805
sage: K(6).global_height()
1.79175946922805
sage: L.<b> = NumberField((a^2).minpoly())
sage: L.degree()
2
sage: b.global_height() # element of L (degree 2 field)
1.41660667202811
sage: (a^2).global_height() # element of K (degree 4 field)
1.41660667202811
Returns the total archimedean component of the height of self.
INPUT:
OUTPUT:
(real) The total archimedean component of the height of this number field element; that is, the sum of the local heights at all infinite places.
EXAMPLES:
sage: R.<x> = QQ[]
sage: K.<a> = NumberField(x^4+3*x^2-17)
sage: b = a/2
sage: b.global_height_arch()
0.38653407379277...
Returns the total non-archimedean component of the height of self.
INPUT:
OUTPUT:
(real) The total non-archimedean component of the height of this number field element; that is, the sum of the local heights at all finite places, weighted by the local degrees.
ALGORITHM:
An alternative formula is 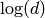 where
where 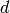 is the norm of
the denominator ideal; this is used to avoid factorization.
is the norm of
the denominator ideal; this is used to avoid factorization.
EXAMPLES:
sage: R.<x> = QQ[]
sage: K.<a> = NumberField(x^4+3*x^2-17)
sage: b = a/6
sage: b.global_height_non_arch()
7.16703787691222
Check that this is equal to the sum of the non-archimedean local heights:
sage: [b.local_height(P) for P in b.support()]
[0.000000000000000, 0.693147180559945, 1.09861228866811, 1.09861228866811]
sage: [b.local_height(P, weighted=True) for P in b.support()]
[0.000000000000000, 2.77258872223978, 2.19722457733622, 2.19722457733622]
sage: sum([b.local_height(P,weighted=True) for P in b.support()])
7.16703787691222
A relative example:
sage: PK.<y> = K[]
sage: L.<c> = NumberField(y^2 + a)
sage: (c/10).global_height_non_arch()
18.4206807439524
Returns the inverse of self mod the integral ideal I.
INPUT:
NOTE: It’s not implemented yet for non-integral elements.
EXAMPLES:
sage: k.<a> = NumberField(x^2 + 23)
sage: N = k.ideal(3)
sage: d = 3*a + 1
sage: d.inverse_mod(N)
1
sage: k.<a> = NumberField(x^3 + 11)
sage: d = a + 13
sage: d.inverse_mod(a^2)*d - 1 in k.ideal(a^2)
True
sage: d.inverse_mod((5, a + 1))*d - 1 in k.ideal(5, a + 1)
True
sage: K.<b> = k.extension(x^2 + 3)
sage: b.inverse_mod([37, a - b])
7
sage: 7*b - 1 in K.ideal(37, a - b)
True
sage: b.inverse_mod([37, a - b]).parent() == K
True
Determine if a number is in the ring of integers of this number field.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 23)
sage: a.is_integral()
True
sage: t = (1+a)/2
sage: t.is_integral()
True
sage: t.minpoly()
x^2 - x + 6
sage: t = a/2
sage: t.is_integral()
False
sage: t.minpoly()
x^2 + 23/4
An example in a relative extension:
sage: K.<a,b> = NumberField([x^2+1, x^2+3])
sage: (a+b).is_integral()
True
sage: ((a-b)/2).is_integral()
False
Return True if self is a square in its parent number field and otherwise return False.
INPUT:
EXAMPLES:
sage: m.<b> = NumberField(x^4 - 1789)
sage: b.is_square()
False
sage: c = (2/3*b + 5)^2; c
4/9*b^2 + 20/3*b + 25
sage: c.is_square()
True
sage: c.is_square(True)
(True, 2/3*b + 5)
We also test the functional notation.
sage: is_square(c, True)
(True, 2/3*b + 5)
sage: is_square(c)
True
sage: is_square(c+1)
False
Returns True if self is positive for all real embeddings of its parent number field. We do nothing at complex places, so e.g. any element of a totally complex number field will return True.
EXAMPLES:
sage: F.<b> = NumberField(x^3-3*x-1)
sage: b.is_totally_positive()
False
sage: (b^2).is_totally_positive()
True
Returns the local height of self at a given prime ideal 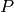 .
.
INPUT:
OUTPUT:
(real) The local height of this number field element at the
place 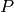 . If weighted is True, this is multiplied by the
local degree (as required for global heights).
. If weighted is True, this is multiplied by the
local degree (as required for global heights).
EXAMPLES:
sage: R.<x> = QQ[]
sage: K.<a> = NumberField(x^4+3*x^2-17)
sage: P = K.ideal(61).factor()[0][0]
sage: b = 1/(a^2 + 30)
sage: b.local_height(P)
4.11087386417331
sage: b.local_height(P, weighted=True)
8.22174772834662
sage: b.local_height(P, 200)
4.1108738641733112487513891034256147463156817430812610629374
sage: (b^2).local_height(P)
8.22174772834662
sage: (b^-1).local_height(P)
0.000000000000000
A relative example:
sage: PK.<y> = K[]
sage: L.<c> = NumberField(y^2 + a)
sage: L(1/4).local_height(L.ideal(2, c-a+1))
1.38629436111989
Returns the local height of self at the  ‘th infinite place.
‘th infinite place.
INPUT:
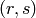 is the
is thesignature of the parent field (so  is the degree).
is the degree).
prec (int) – desired floating point precision (default: default RealField precision).
weighted (bool, default False) – if True, apply local degree weighting, i.e. double the value for complex places.
OUTPUT:
(real) The archimedean local height of this number field
element at the  ‘th infinite place. If weighted is
True, this is multiplied by the local degree (as required for
global heights), i.e. 1 for real places and 2 for complex
places.
‘th infinite place. If weighted is
True, this is multiplied by the local degree (as required for
global heights), i.e. 1 for real places and 2 for complex
places.
EXAMPLES:
sage: R.<x> = QQ[]
sage: K.<a> = NumberField(x^4+3*x^2-17)
sage: [p.codomain() for p in K.places()]
[Real Field with 106 bits of precision,
Real Field with 106 bits of precision,
Complex Field with 53 bits of precision]
sage: [a.local_height_arch(i) for i in range(3)]
[0.5301924545717755083366563897519,
0.5301924545717755083366563897519,
0.886414217456333]
sage: [a.local_height_arch(i, weighted=True) for i in range(3)]
[0.5301924545717755083366563897519,
0.5301924545717755083366563897519,
1.77282843491267]
A relative example:
sage: L.<b, c> = NumberFieldTower([x^2 - 5, x^3 + x + 3])
sage: [(b + c).local_height_arch(i) for i in range(4)]
[1.238223390757884911842206617439,
0.02240347229957875780769746914391,
0.780028961749618,
1.16048938497298]
If base is None, return the matrix of right multiplication by the
element on the power basis 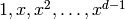 for
the number field. Thus the rows of this matrix give the images of
each of the
for
the number field. Thus the rows of this matrix give the images of
each of the 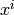 .
.
If base is not None, then base must be either a field that embeds in the parent of self or a morphism to the parent of self, in which case this function returns the matrix of multiplication by self on the power basis, where we view the parent field as a field over base.
INPUT:
EXAMPLES:
Regular number field:
sage: K.<a> = NumberField(QQ['x'].0^3 - 5)
sage: M = a.matrix(); M
[0 1 0]
[0 0 1]
[5 0 0]
sage: M.base_ring() is QQ
True
Relative number field:
sage: L.<b> = K.extension(K['x'].0^2 - 2)
sage: M = b.matrix(); M
[0 1]
[2 0]
sage: M.base_ring() is K
True
Absolute number field:
sage: M = L.absolute_field('c').gen().matrix(); M
[ 0 1 0 0 0 0]
[ 0 0 1 0 0 0]
[ 0 0 0 1 0 0]
[ 0 0 0 0 1 0]
[ 0 0 0 0 0 1]
[-17 -60 -12 -10 6 0]
sage: M.base_ring() is QQ
True
More complicated relative number field:
sage: L.<b> = K.extension(K['x'].0^2 - a); L
Number Field in b with defining polynomial x^2 - a over its base field
sage: M = b.matrix(); M
[0 1]
[a 0]
sage: M.base_ring() is K
True
An example where we explicitly give the subfield or the embedding:
sage: K.<a> = NumberField(x^4 + 1); L.<a2> = NumberField(x^2 + 1)
sage: a.matrix(L)
[ 0 1]
[a2 0]
Notice that if we compute all embeddings and choose a different one, then the matrix is changed as it should be:
sage: v = L.embeddings(K)
sage: a.matrix(v[1])
[ 0 1]
[-a2 0]
The norm is also changed:
sage: a.norm(v[1])
a2
sage: a.norm(v[0])
-a2
TESTS:
sage: F.<z> = CyclotomicField(5) ; t = 3*z**3 + 4*z**2 + 2
sage: t.matrix(F)
[3*z^3 + 4*z^2 + 2]
Return the minimal polynomial of this number field element.
EXAMPLES:
sage: K.<a> = NumberField(x^2+3)
sage: a.minpoly('x')
x^2 + 3
sage: R.<X> = K['X']
sage: L.<b> = K.extension(X^2-(22 + a))
sage: b.minpoly('t')
t^2 - a - 22
sage: b.absolute_minpoly('t')
t^4 - 44*t^2 + 487
sage: b^2 - (22+a)
0
Return the multiplicative order of this number field element.
EXAMPLES:
sage: K.<z> = CyclotomicField(5)
sage: z.multiplicative_order()
5
sage: (-z).multiplicative_order()
10
sage: (1+z).multiplicative_order()
+Infinity
sage: x = polygen(QQ)
sage: K.<a>=NumberField(x^40 - x^20 + 4)
sage: u = 1/4*a^30 + 1/4*a^10 + 1/2
sage: u.multiplicative_order()
6
sage: a.multiplicative_order()
+Infinity
An example in a relative extension:
sage: K.<a, b> = NumberField([x^2 + x + 1, x^2 - 3])
sage: z = (a - 1)*b/3
sage: z.multiplicative_order()
12
sage: z^12==1 and z^6!=1 and z^4!=1
True
Return the absolute or relative norm of this number field element.
If K is given then K must be a subfield of the parent L of self, in which case the norm is the relative norm from L to K. In all other cases, the norm is the absolute norm down to QQ.
EXAMPLES:
sage: K.<a> = NumberField(x^3 + x^2 + x - 132/7); K
Number Field in a with defining polynomial x^3 + x^2 + x - 132/7
sage: a.norm()
132/7
sage: factor(a.norm())
2^2 * 3 * 7^-1 * 11
sage: K(0).norm()
0
Some complicated relatives norms in a tower of number fields.
sage: K.<a,b,c> = NumberField([x^2 + 1, x^2 + 3, x^2 + 5])
sage: L = K.base_field(); M = L.base_field()
sage: a.norm()
1
sage: a.norm(L)
1
sage: a.norm(M)
1
sage: a
a
sage: (a+b+c).norm()
121
sage: (a+b+c).norm(L)
2*c*b - 7
sage: (a+b+c).norm(M)
-11
We illustrate that norm is compatible with towers:
sage: z = (a+b+c).norm(L); z.norm(M)
-11
If we are in an order, the norm is an integer:
sage: K.<a> = NumberField(x^3-2)
sage: a.norm().parent()
Rational Field
sage: R = K.ring_of_integers()
sage: R(a).norm().parent()
Integer Ring
TESTS:
sage: F.<z> = CyclotomicField(5)
sage: t = 3*z**3 + 4*z**2 + 2
sage: t.norm(F)
3*z^3 + 4*z^2 + 2
Return an nth root of self in the given number field.
EXAMPLES:
sage: K.<a> = NumberField(x^4-7)
sage: K(7).nth_root(2)
a^2
sage: K((a-3)^5).nth_root(5)
a - 3
ALGORITHM: Use Pari to factor 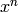 - self
in K.
- self
in K.
Return the numerator ideal of this number field element.
Note
A ValueError will be raised if this function is called on 0.
Note
See also denominator_ideal()
OUTPUT:
(integral ideal) The numerator ideal  of this element,
where for a non-zero number field element
of this element,
where for a non-zero number field element  , the principal
ideal generated by
, the principal
ideal generated by  has the form
has the form 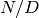 where
where  and
and  are coprime integral ideals. An error is raised if the
element is zero.
are coprime integral ideals. An error is raised if the
element is zero.
EXAMPLES:
sage: K.<a> = NumberField(x^2+5)
sage: b = (1+a)/2
sage: b.norm()
3/2
sage: N = b.numerator_ideal(); N
Fractional ideal (3, a + 1)
sage: N.norm()
3
sage: (1/b).numerator_ideal()
Fractional ideal (2, a + 1)
TESTS:
Undefined for 0:
sage: K(0).numerator_ideal()
...
ValueError: numerator ideal of 0 is not defined.
Return the underlying polynomial corresponding to this number field element.
The resulting polynomial is currently not cached.
EXAMPLES:
sage: K.<a> = NumberField(x^5 - x - 1)
sage: f = (-2/3 + 1/3*a)^4; f
1/81*a^4 - 8/81*a^3 + 8/27*a^2 - 32/81*a + 16/81
sage: g = f.polynomial(); g
1/81*x^4 - 8/81*x^3 + 8/27*x^2 - 32/81*x + 16/81
sage: parent(g)
Univariate Polynomial Ring in x over Rational Field
Note that the result of this function is not cached (should this be changed?):
sage: g is f.polynomial()
False
Returns the square root of this number in the given number field.
EXAMPLES:
sage: K.<a> = NumberField(x^2 - 3)
sage: K(3).sqrt()
a
sage: K(3).sqrt(all=True)
[a, -a]
sage: K(a^10).sqrt()
9*a
sage: K(49).sqrt()
7
sage: K(1+a).sqrt()
...
ValueError: a + 1 not a square in Number Field in a with defining polynomial x^2 - 3
sage: K(0).sqrt()
0
sage: K((7+a)^2).sqrt(all=True)
[a + 7, -a - 7]
sage: K.<a> = CyclotomicField(7)
sage: a.sqrt()
a^4
sage: K.<a> = NumberField(x^5 - x + 1)
sage: (a^4 + a^2 - 3*a + 2).sqrt()
a^3 - a^2
ALGORITHM: Use Pari to factor 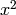 - self
in K.
- self
in K.
Return the support of this number field element.
OUTPUT: A sorted list of the primes ideals at which this number field element has nonzero valuation. An error is raised if the element is zero.
EXAMPLES:
sage: x = ZZ['x'].gen()
sage: F.<t> = NumberField(x^3 - 2)
sage: P5s = F(5).support()
sage: P5s
[Fractional ideal (-t^2 - 1), Fractional ideal (t^2 - 2*t - 1)]
sage: all(5 in P5 for P5 in P5s)
True
sage: all(P5.is_prime() for P5 in P5s)
True
sage: [ P5.norm() for P5 in P5s ]
[5, 25]
TESTS:
It doesn’t make sense to factor the ideal (0):
sage: F(0).support()
...
ArithmeticError: Support of 0 is not defined.
Return the absolute or relative trace of this number field element.
If K is given then K must be a subfield of the parent L of self, in which case the trace is the relative trace from L to K. In all other cases, the trace is the absolute trace down to QQ.
EXAMPLES:
sage: K.<a> = NumberField(x^3 -132/7*x^2 + x + 1); K
Number Field in a with defining polynomial x^3 - 132/7*x^2 + x + 1
sage: a.trace()
132/7
sage: (a+1).trace() == a.trace() + 3
True
If we are in an order, the trace is an integer:
sage: K.<zeta> = CyclotomicField(17)
sage: R = K.ring_of_integers()
sage: R(zeta).trace().parent()
Integer Ring
TESTS:
sage: F.<z> = CyclotomicField(5) ; t = 3*z**3 + 4*z**2 + 2
sage: t.trace(F)
3*z^3 + 4*z^2 + 2
Returns the valuation of self at a given prime ideal P.
INPUT:
EXAMPLES:
sage: R.<x> = QQ[]
sage: K.<a> = NumberField(x^4+3*x^2-17)
sage: P = K.ideal(61).factor()[0][0]
sage: b = a^2 + 30
sage: b.valuation(P)
1
sage: type(b.valuation(P))
<type 'sage.rings.integer.Integer'>
The function can be applied to elements in relative number fields:
sage: L.<b> = K.extension(x^2 - 3)
sage: [L(6).valuation(P) for P in L.primes_above(2)]
[4]
sage: [L(6).valuation(P) for P in L.primes_above(3)]
[2, 2]
Return vector representation of self in terms of the basis for the ambient number field.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 1)
sage: (2/3*a - 5/6).vector()
(-5/6, 2/3)
sage: (-5/6, 2/3)
(-5/6, 2/3)
sage: O = K.order(2*a)
sage: (O.1).vector()
(0, 2)
sage: K.<a,b> = NumberField([x^2 + 1, x^2 - 3])
sage: (a + b).vector()
(b, 1)
sage: O = K.order([a,b])
sage: (O.1).vector()
(-b, 1)
sage: (O.2).vector()
(1, -b)
Bases: sage.rings.number_field.number_field_element.NumberFieldElement
Return the characteristic polynomial of this element over
For the meaning of the optional argument algorithm, see charpoly().
EXAMPLES:
sage: x = ZZ['x'].0
sage: K.<a> = NumberField(x^4 + 2, 'a')
sage: a.absolute_charpoly()
x^4 + 2
sage: a.absolute_charpoly('y')
y^4 + 2
sage: (-a^2).absolute_charpoly()
x^4 + 4*x^2 + 4
sage: (-a^2).absolute_minpoly()
x^2 + 2
sage: a.absolute_charpoly(algorithm='pari') == a.absolute_charpoly(algorithm='sage')
True
Return the minimal polynomial of this element over
 .
.
For the meaning of the optional argument algorithm, see charpoly().
EXAMPLES:
sage: x = ZZ['x'].0
sage: f = x^10 - 5*x^9 + 15*x^8 - 68*x^7 + 81*x^6 - 221*x^5 + 141*x^4 - 242*x^3 - 13*x^2 - 33*x - 135
sage: K.<a> = NumberField(f, 'a')
sage: a.absolute_charpoly()
x^10 - 5*x^9 + 15*x^8 - 68*x^7 + 81*x^6 - 221*x^5 + 141*x^4 - 242*x^3 - 13*x^2 - 33*x - 135
sage: a.absolute_charpoly('y')
y^10 - 5*y^9 + 15*y^8 - 68*y^7 + 81*y^6 - 221*y^5 + 141*y^4 - 242*y^3 - 13*y^2 - 33*y - 135
sage: b = -79/9995*a^9 + 52/9995*a^8 + 271/9995*a^7 + 1663/9995*a^6 + 13204/9995*a^5 + 5573/9995*a^4 + 8435/1999*a^3 - 3116/9995*a^2 + 7734/1999*a + 1620/1999
sage: b.absolute_charpoly()
x^10 + 10*x^9 + 25*x^8 - 80*x^7 - 438*x^6 + 80*x^5 + 2950*x^4 + 1520*x^3 - 10439*x^2 - 5130*x + 18225
sage: b.absolute_minpoly()
x^5 + 5*x^4 - 40*x^2 - 19*x + 135
sage: b.absolute_minpoly(algorithm='pari') == b.absolute_minpoly(algorithm='sage')
True
The characteristic polynomial of this element, over
 if self is an element of a field, and over
if self is an element of a field, and over
 is self is an element of an order.
is self is an element of an order.
This is the same as self.absolute_charpoly since this is an element of an absolute extension.
The optional argument algorithm controls how the characteristic polynomial is computed: ‘pari’ uses Pari, ‘sage’ uses charpoly for Sage matrices. The default value None means that ‘pari’ is used for small degrees (up to the value of the constant TUNE_CHARPOLY_NF, currently at 25), otherwise ‘sage’ is used. The constant TUNE_CHARPOLY_NF should give reasonable performance on all architectures; however, if you feel the need to customize it to your own machine, see trac ticket 5213 for a tuning script.
EXAMPLES:
We compute the characteristic polynomial of the cube root of  .
.
sage: R.<x> = QQ[]
sage: K.<a> = NumberField(x^3-2)
sage: a.charpoly('x')
x^3 - 2
sage: a.charpoly('y').parent()
Univariate Polynomial Ring in y over Rational Field
TESTS:
sage: R = K.ring_of_integers()
sage: R(a).charpoly()
x^3 - 2
sage: R(a).charpoly().parent()
Univariate Polynomial Ring in x over Integer Ring
sage: R(a).charpoly(algorithm='pari') == R(a).charpoly(algorithm='sage')
True
Using the n method of approximation, return True if self is a real positive number and False otherwise. This method is completely dependent of the embedding used by the n method.
The algorithm first checks that self is not a strictly
complex number. Then if self is not zero, by approximation
more and more precise, the method answers True if the
number is positive. Using 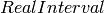 , the result is
guaranteed to be correct.
, the result is
guaranteed to be correct.
For CyclotomicField, the embedding is the natural one
sending 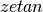 on
on 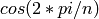 .
.
EXAMPLES:
sage: K.<a> = CyclotomicField(3)
sage: (a+a^2).is_real_positive()
False
sage: (-a-a^2).is_real_positive()
True
sage: K.<a> = CyclotomicField(1000)
sage: (a+a^(-1)).is_real_positive()
True
sage: K.<a> = CyclotomicField(1009)
sage: d = a^252
sage: (d+d.conjugate()).is_real_positive()
True
sage: d = a^253
sage: (d+d.conjugate()).is_real_positive()
False
sage: K.<a> = QuadraticField(3)
sage: a.is_real_positive()
True
sage: K.<a> = QuadraticField(-3)
sage: a.is_real_positive()
False
sage: (a-a).is_real_positive()
False
Return an element of QQ[x], where this number field element lives in QQ[x]/(f(x)).
Return the list of coefficients of self written in terms of a power basis.
EXAMPLE:
sage: K.<z> = CyclotomicField(3)
sage: (2+3/5*z).list()
[2, 3/5]
sage: (5*z).list()
[0, 5]
sage: K(3).list()
[3, 0]
Return the minimal polynomial of this number field element.
For the meaning of the optional argument algorithm, see charpoly().
EXAMPLES:
We compute the characteristic polynomial of cube root of  .
.
sage: R.<x> = QQ[]
sage: K.<a> = NumberField(x^3-2)
sage: a.minpoly('x')
x^3 - 2
sage: a.minpoly('y').parent()
Univariate Polynomial Ring in y over Rational Field
TESTS:
sage: R = K.ring_of_integers()
sage: R(a).minpoly()
x^3 - 2
sage: R(a).minpoly().parent()
Univariate Polynomial Ring in x over Integer Ring
sage: R(a).minpoly(algorithm='pari') == R(a).minpoly(algorithm='sage')
True
Bases: sage.rings.number_field.number_field_element.NumberFieldElement
The current relative number field element implementation does everything in terms of absolute polynomials.
All conversions from relative polynomials, lists, vectors, etc should happen in the parent.
The characteristic polynomial of this element over
 .
.
We construct a relative extension and find the characteristic
polynomial over  .
.
The optional argument algorithm controls how the characteristic polynomial is computed: ‘pari’ uses Pari, ‘sage’ uses charpoly for Sage matrices. The default value None means that ‘pari’ is used for small degrees (up to the value of the constant TUNE_CHARPOLY_NF, currently at 25), otherwise ‘sage’ is used. The constant TUNE_CHARPOLY_NF should give reasonable performance on all architectures; however, if you feel the need to customize it to your own machine, see trac ticket 5213 for a tuning script.
EXAMPLES:
sage: R.<x> = QQ[]
sage: K.<a> = NumberField(x^3-2)
sage: S.<X> = K[]
sage: L.<b> = NumberField(X^3 + 17); L
Number Field in b with defining polynomial X^3 + 17 over its base field
sage: b.absolute_charpoly()
x^9 + 51*x^6 + 867*x^3 + 4913
sage: b.charpoly()(b)
0
sage: a = L.0; a
b
sage: a.absolute_charpoly('x')
x^9 + 51*x^6 + 867*x^3 + 4913
sage: a.absolute_charpoly('y')
y^9 + 51*y^6 + 867*y^3 + 4913
sage: a.absolute_charpoly(algorithm='pari') == a.absolute_charpoly(algorithm='sage')
True
Return the minimal polynomial over  of this element.
of this element.
For the meaning of the optional argument algorithm, see absolute_charpoly().
EXAMPLES:
sage: K.<a, b> = NumberField([x^2 + 2, x^2 + 1000*x + 1])
sage: y = K['y'].0
sage: L.<c> = K.extension(y^2 + a*y + b)
sage: c.absolute_charpoly()
x^8 - 1996*x^6 + 996006*x^4 + 1997996*x^2 + 1
sage: c.absolute_minpoly()
x^8 - 1996*x^6 + 996006*x^4 + 1997996*x^2 + 1
sage: L(a).absolute_charpoly()
x^8 + 8*x^6 + 24*x^4 + 32*x^2 + 16
sage: L(a).absolute_minpoly()
x^2 + 2
sage: L(b).absolute_charpoly()
x^8 + 4000*x^7 + 6000004*x^6 + 4000012000*x^5 + 1000012000006*x^4 + 4000012000*x^3 + 6000004*x^2 + 4000*x + 1
sage: L(b).absolute_minpoly()
x^2 + 1000*x + 1
The characteristic polynomial of this element over its base field.
EXAMPLES:
sage: x = ZZ['x'].0
sage: K.<a, b> = QQ.extension([x^2 + 2, x^5 + 400*x^4 + 11*x^2 + 2])
sage: a.charpoly()
x^2 + 2
sage: b.charpoly()
x^2 - 2*b*x + b^2
sage: b.minpoly()
x - b
sage: K.<a, b> = NumberField([x^2 + 2, x^2 + 1000*x + 1])
sage: y = K['y'].0
sage: L.<c> = K.extension(y^2 + a*y + b)
sage: c.charpoly()
x^2 + a*x + b
sage: c.minpoly()
x^2 + a*x + b
sage: L(a).charpoly()
x^2 - 2*a*x - 2
sage: L(a).minpoly()
x - a
sage: L(b).charpoly()
x^2 - 2*b*x - 1000*b - 1
sage: L(b).minpoly()
x - b
Return an element of K[x], where this number field element lives in the relative number field K[x]/(f(x)).
Return the list of coefficients of self written in terms of a power basis.
EXAMPLES:
sage: K.<a,b> = NumberField([x^3+2, x^2+1])
sage: a.list()
[0, 1, 0]
sage: v = (K.base_field().0 + a)^2 ; v
a^2 + 2*b*a - 1
sage: v.list()
[-1, 2*b, 1]
Returns the valuation of self at a given prime ideal P.
INPUT:
EXAMPLES:
sage: K.<a, b, c> = NumberField([x^2 - 2, x^2 - 3, x^2 - 5])
sage: P = K.prime_factors(5)[0]
sage: (2*a + b - c).valuation(P)
1
Bases: sage.rings.number_field.number_field_element.NumberFieldElement_absolute
Element of an order in an absolute number field.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 1)
sage: O2 = K.order(2*a)
sage: w = O2.1; w
2*a
sage: parent(w)
Order in Number Field in a with defining polynomial x^2 + 1
sage: w.absolute_charpoly()
x^2 + 4
sage: w.absolute_charpoly().parent()
Univariate Polynomial Ring in x over Integer Ring
sage: w.absolute_minpoly()
x^2 + 4
sage: w.absolute_minpoly().parent()
Univariate Polynomial Ring in x over Integer Ring
Return an inverse of self modulo the given ideal.
INPUT:
EXAMPLES:
sage: OE = NumberField(x^3 - x + 2, 'w').ring_of_integers()
sage: w = OE.ring_generators()[0]
sage: w.inverse_mod(13*OE)
6*w^2 - 6
sage: w * (w.inverse_mod(13)) - 1 in 13*OE
True
sage: w.inverse_mod(13).parent() == OE
True
sage: w.inverse_mod(2*OE)
...
ZeroDivisionError: w is not invertible modulo Fractional ideal (2)
Bases: sage.rings.number_field.number_field_element.NumberFieldElement_relative
Element of an order in a relative number field.
EXAMPLES:
sage: O = EquationOrder([x^2 + x + 1, x^3 - 2],'a,b')
sage: c = O.1; c
(-2*b^2 - 2)*a - 2*b^2 - b
sage: type(c)
<type 'sage.rings.number_field.number_field_element.OrderElement_relative'>
The absolute characteristic polynomial of this order element over ZZ.
EXAMPLES:
sage: x = ZZ['x'].0
sage: K.<a,b> = NumberField([x^2 + 1, x^2 - 3])
sage: OK = K.maximal_order()
sage: _, u, _, v = OK.basis()
sage: t = 2*u - v; t
-b
sage: t.absolute_charpoly()
x^4 - 6*x^2 + 9
sage: t.absolute_minpoly()
x^2 - 3
sage: t.absolute_charpoly().parent()
Univariate Polynomial Ring in x over Integer Ring
The absolute minimal polynomial of this order element over ZZ.
EXAMPLES:
sage: x = ZZ['x'].0
sage: K.<a,b> = NumberField([x^2 + 1, x^2 - 3])
sage: OK = K.maximal_order()
sage: _, u, _, v = OK.basis()
sage: t = 2*u - v; t
-b
sage: t.absolute_charpoly()
x^4 - 6*x^2 + 9
sage: t.absolute_minpoly()
x^2 - 3
sage: t.absolute_minpoly().parent()
Univariate Polynomial Ring in x over Integer Ring
The characteristic polynomial of this order element over its base ring.
This special implementation works around bug #4738. At this time the base ring of relative order elements is ZZ; it should be the ring of integers of the base field.
EXAMPLES:
sage: x = ZZ['x'].0
sage: K.<a,b> = NumberField([x^2 + 1, x^2 - 3])
sage: OK = K.maximal_order(); OK.basis()
[1, 1/2*a - 1/2*b, -1/2*b*a + 1/2, a]
sage: charpoly(OK.1)
x^2 + b*x + 1
sage: charpoly(OK.1).parent()
Univariate Polynomial Ring in x over Maximal Order in Number Field in b with defining polynomial x^2 - 3
sage: [ charpoly(t) for t in OK.basis() ]
[x^2 - 2*x + 1, x^2 + b*x + 1, x^2 - x + 1, x^2 + 1]
Return an inverse of self modulo the given ideal.
INPUT:
EXAMPLES:
sage: E.<a,b> = NumberField([x^2 - x + 2, x^2 + 1])
sage: OE = E.ring_of_integers()
sage: t = OE(b - a).inverse_mod(17*b)
sage: t*(b - a) - 1 in E.ideal(17*b)
True
sage: t.parent() == OE
True
The minimal polynomial of this order element over its base ring.
This special implementation works around bug #4738. At this time the base ring of relative order elements is ZZ; it should be the ring of integers of the base field.
EXAMPLES:
sage: x = ZZ['x'].0
sage: K.<a,b> = NumberField([x^2 + 1, x^2 - 3])
sage: OK = K.maximal_order(); OK.basis()
[1, 1/2*a - 1/2*b, -1/2*b*a + 1/2, a]
sage: minpoly(OK.1)
x^2 + b*x + 1
sage: charpoly(OK.1).parent()
Univariate Polynomial Ring in x over Maximal Order in Number Field in b with defining polynomial x^2 - 3
sage: _, u, _, v = OK.basis()
sage: t = 2*u - v; t
-b
sage: t.charpoly()
x^2 + 2*b*x + 3
sage: t.minpoly()
x + b
sage: t.absolute_charpoly()
x^4 - 6*x^2 + 9
sage: t.absolute_minpoly()
x^2 - 3
Return True if x is of type NumberFieldElement, i.e., an element of a number field.
EXAMPLES:
sage: from sage.rings.number_field.number_field_element import is_NumberFieldElement
sage: is_NumberFieldElement(2)
False
sage: k.<a> = NumberField(x^7 + 17*x + 1)
sage: is_NumberFieldElement(a+1)
True