This file defines a Cython class NumberFieldElement_quadratic to speed up
computations in quadratic extensions of  .
.
AUTHORS:
TODO:
The _new() method should be overridden in this class to copy the D attribute
Bases: sage.rings.number_field.number_field_element.NumberFieldElement_absolute
A NumberFieldElement_quadratic object gives an efficient representation of
an element of a quadratic extension of  .
.
Elements are represented internally as triples 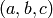 of integers,
where
of integers,
where 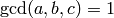 and
and 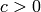 , representing the element
, representing the element 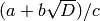 . Note that if the discriminant
. Note that if the discriminant  is
is 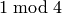 ,
integral elements do not necessarily have
,
integral elements do not necessarily have 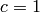 .
.
TESTS:
sage: from sage.rings.number_field.number_field_element_quadratic import NumberFieldElement_quadratic
We set up some fields:
sage: K.<a> = NumberField(x^2+23)
sage: a.parts()
(0, 1)
sage: F.<b> = NumberField(x^2-x+7)
sage: b.parts()
(1/2, 3/2)
We construct elements of these fields in various ways - firstly, from polynomials:
sage: NumberFieldElement_quadratic(K, x-1)
a - 1
sage: NumberFieldElement_quadratic(F, x-1)
b - 1
From triples of Integers:
sage: NumberFieldElement_quadratic(K, (1,2,3))
2/3*a + 1/3
sage: NumberFieldElement_quadratic(F, (1,2,3))
4/9*b + 1/9
sage: NumberFieldElement_quadratic(F, (1,2,3)).parts()
(1/3, 2/3)
From pairs of Rationals:
sage: NumberFieldElement_quadratic(K, (1/2,1/3))
1/3*a + 1/2
sage: NumberFieldElement_quadratic(F, (1/2,1/3))
2/9*b + 7/18
sage: NumberFieldElement_quadratic(F, (1/2,1/3)).parts()
(1/2, 1/3)
Direct from Rationals:
sage: NumberFieldElement_quadratic(K, 2/3)
2/3
sage: NumberFieldElement_quadratic(F, 2/3)
2/3
This checks a bug when converting from lists:
sage: w = CyclotomicField(3)([1/2,1])
sage: w == w.__invert__().__invert__()
True
The characteristic polynomial of this element over  .
.
EXAMPLES:
sage: K.<a> = NumberField(x^2-x+13)
sage: a.charpoly()
x^2 - x + 13
sage: b = 3-a/2
sage: f = b.charpoly(); f
x^2 - 11/2*x + 43/4
sage: f(b)
0
Return the denominator of self. This is the LCM of the denominators of
the coefficients of self, and thus it may well be 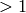 even when the
element is an algebraic integer.
even when the
element is an algebraic integer.
EXAMPLES:
sage: K.<a> = NumberField(x^2+x+41)
sage: a.denominator()
1
sage: b = (2*a+1)/6
sage: b.denominator()
6
sage: K(1).denominator()
1
sage: K(1/2).denominator()
2
sage: K(0).denominator()
1
sage: K.<a> = NumberField(x^2 - 5)
sage: b = (a + 1)/2
sage: b.denominator()
2
sage: b.is_integral()
True
Returns the imaginary part of self.
EXAMPLES:
sage: K.<sqrt2> = QuadraticField(2)
sage: sqrt2.imag()
0
sage: parent(sqrt2.imag())
Rational Field
sage: K.<i> = QuadraticField(-1)
sage: i.imag()
1
sage: parent(i.imag())
Rational Field
sage: K.<a> = NumberField(x^2 + x + 1, embedding=CDF.0)
sage: a.imag()
1/2*sqrt3
sage: a.real()
-1/2
sage: SR(a)
1/2*I*sqrt(3) - 1/2
sage: bool(I*a.imag() + a.real() == a)
True
TESTS:
sage: K.<a> = QuadraticField(-9, embedding=-CDF.0)
sage: a.imag()
-3
sage: parent(a.imag())
Rational Field
Returns whether this element is an algebraic integer.
TESTS:
sage: K.<a> = QuadraticField(-1)
sage: a.is_integral()
True
sage: K(1).is_integral()
True
sage: K(1/2).is_integral()
False
sage: K(a/2).is_integral()
False
sage: K((a+1)/2).is_integral()
False
sage: K(a/3).is_integral()
False
sage: K.<a> = QuadraticField(-3)
sage: a.is_integral()
True
sage: K(1).is_integral()
True
sage: K(1/2).is_integral()
False
sage: K(a/2).is_integral()
False
sage: ((a+1)/2).is_integral()
True
The minimal polynomial of this element over  .
.
EXAMPLES:
sage: K.<a> = NumberField(x^2+13)
sage: a.minpoly()
x^2 + 13
sage: (a+1/2-a).minpoly()
x - 1/2
Return the norm of self. If the second argument is None, this is the
norm down to  . Otherwise, return the norm down to K (which had
better be either
. Otherwise, return the norm down to K (which had
better be either  or this number field).
or this number field).
EXAMPLES:
sage: K.<a> = NumberField(x^2-x+3)
sage: a.norm()
3
sage: a.matrix()
[ 0 1]
[-3 1]
sage: K.<a> = NumberField(x^2+5)
sage: (1+a).norm()
6
The norm is multiplicative:
sage: K.<a> = NumberField(x^2-3)
sage: a.norm()
-3
sage: K(3).norm()
9
sage: (3*a).norm()
-27
We test that the optional argument is handled sensibly:
sage: (3*a).norm(QQ)
-27
sage: (3*a).norm(K)
3*a
sage: (3*a).norm(CyclotomicField(3))
...
ValueError: no way to embed L into parent's base ring K
This function returns a pair of rationals  and
and  such that self
such that self 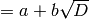 .
.
This is much closer to the internal storage format of the
elements than the polynomial representation coefficients (the output of
self.list()), unless the generator with which this number field was
constructed was equal to 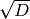 . See the last example below.
. See the last example below.
EXAMPLES:
sage: K.<a> = NumberField(x^2-13)
sage: K.discriminant()
13
sage: a.parts()
(0, 1)
sage: (a/2-4).parts()
(-4, 1/2)
sage: K.<a> = NumberField(x^2-7)
sage: K.discriminant()
28
sage: a.parts()
(0, 1)
sage: K.<a> = NumberField(x^2-x+7)
sage: a.parts()
(1/2, 3/2)
sage: a._coefficients()
[0, 1]
Returns the real part of self, which is either self (if self lives it a totally real field) or a rational number.
EXAMPLES:
sage: K.<sqrt2> = QuadraticField(2)
sage: sqrt2.real()
sqrt2
sage: K.<a> = QuadraticField(-3)
sage: a.real()
0
sage: (a + 1/2).real()
1/2
sage: K.<a> = NumberField(x^2 + x + 1)
sage: a.real()
-1/2
sage: parent(a.real())
Rational Field
sage: K.<i> = QuadraticField(-1)
sage: i.real()
0
EXAMPLES:
sage: K.<a> = NumberField(x^2+x+41)
sage: a.trace()
-1
sage: a.matrix()
[ 0 1]
[-41 -1]
The trace is additive:
sage: K.<a> = NumberField(x^2+7)
sage: (a+1).trace()
2
sage: K(3).trace()
6
sage: (a+4).trace()
8
sage: (a/3+1).trace()
2
Bases: sage.rings.number_field.number_field_element_quadratic.NumberFieldElement_quadratic
Element of an order in a quadratic field.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 1)
sage: O2 = K.order(2*a)
sage: w = O2.1; w
2*a
sage: parent(w)
Order in Number Field in a with defining polynomial x^2 + 1
The characteristic polynomial of this element, which is over  because this element is an algebraic integer.
because this element is an algebraic integer.
EXAMPLES:
sage: K.<a> = NumberField(x^2 - 5)
sage: R = K.ring_of_integers()
sage: b = R((5+a)/2)
sage: f = b.charpoly('x'); f
x^2 - 5*x + 5
sage: f.parent()
Univariate Polynomial Ring in x over Integer Ring
sage: f(b)
0
Return an inverse of self modulo the given ideal.
INPUT:
EXAMPLES:
sage: OE = QuadraticField(-7, 's').ring_of_integers()
sage: w = OE.ring_generators()[0]
sage: w.inverse_mod(13) == 6*w - 6
True
sage: w*(6*w - 6) - 1
-13
sage: w.inverse_mod(13).parent() == OE
True
sage: w.inverse_mod(2*OE)
...
ZeroDivisionError: 1/2*s + 1/2 is not invertible modulo Fractional ideal (2)
The minimal polynomial of this element over  .
.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 163)
sage: R = K.ring_of_integers()
sage: f = R(a).minpoly('x'); f
x^2 + 163
sage: f.parent()
Univariate Polynomial Ring in x over Integer Ring
sage: R(5).minpoly()
x - 5
The norm of an element of the ring of integers is an Integer.
EXAMPLES:
sage: K.<a> = NumberField(x^2 + 3)
sage: O2 = K.order(2*a)
sage: w = O2.gen(1); w
2*a
sage: w.norm()
12
sage: parent(w.norm())
Integer Ring
The trace of an element of the ring of integers is an Integer.
EXAMPLES:
sage: K.<a> = NumberField(x^2 - 5)
sage: R = K.ring_of_integers()
sage: b = R((1+a)/2)
sage: b.trace()
1
sage: parent(b.trace())
Integer Ring
Bases: sage.categories.morphism.Morphism
Morphism that coerces from rationals to elements of a quadratic number field K.