Base class for finite field elements.

AUTHORS:

- David Roe (2010-1-14) -- factored out of sage.structure.element

class sage.rings.finite_rings.element_base.FiniteFieldElement

Bases: sage.structure.element.FieldElement

additive_order()

Return the additive order of this finite field element.

EXAMPLES:

sage: k.<a> = FiniteField(2^12, 'a')
sage: b = a^3 + a + 1
sage: b.additive_order()
2
sage: k(0).additive_order()
1

charpoly(var='x', algorithm='matrix')

Return the characteristic polynomial of self as a polynomial with given variable.

INPUT:

• var - string (default: ‘x’)
• algorithm - string (default: ‘matrix’)
  • ‘matrix’ - return the charpoly computed from the matrix of left multiplication by self
  • ‘pari’ – use pari’s charpoly routine on polymods, which is not very good except in small cases

The result is not cached.

EXAMPLES:

sage: k.<a> = GF(19^2)
sage: parent(a)
Finite Field in a of size 19^2
sage: a.charpoly('X')
X^2 + 18*X + 2
sage: a^2 + 18*a + 2
0            
sage: a.charpoly('X', algorithm='pari')
X^2 + 18*X + 2

frobenius(k=1)

Return the 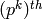power of self, where is the characteristic of the field.

INPUT:

• k - integer (default: 1, must fit in C int type)

Note that if is negative, then this computes the appropriate root.

EXAMPLES:

sage: F.<a> = GF(29^2)
sage: z = a^2 + 5*a + 1
sage: z.pth_power()
19*a + 20
sage: z.pth_power(10)
10*a + 28
sage: z.pth_power(-10) == z
True
sage: F.<b> = GF(2^12)
sage: y = b^3 + b + 1
sage: y == (y.pth_power(-3))^(2^3)
True
sage: y.pth_power(2)
b^7 + b^6 + b^5 + b^4 + b^3 + b

matrix(reverse=False)

See _matrix_().

EXAMPLE:

sage: k.<a> = GF(2^16)
sage: e = a^2 + 1
sage: e.matrix() # random-ish error message
doctest:1: DeprecationWarning:The function matrix is replaced by _matrix_.
[1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0]
[0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
[1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0]
[0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 1]
[0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1]
[0 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0]
[0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1]
[0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0]
[0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0]
[0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0]
[0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0]
[0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0]
[0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0]
[0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0]
[0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0]
[0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1]

minimal_polynomial(var='x')

Returns the minimal polynomial of this element (over the corresponding prime subfield).

EXAMPLES:

sage: k.<a> = FiniteField(3^4)
sage: parent(a)
Finite Field in a of size 3^4
sage: b=a**20;p=charpoly(b,"y");p
y^4 + 2*y^2 + 1 
sage: factor(p)
(y^2 + 1)^2
sage: b.minimal_polynomial('y')
y^2 + 1

minpoly(var='x')

Returns the minimal polynomial of this element (over the corresponding prime subfield).

EXAMPLES:

sage: k.<a> = FiniteField(19^2)
sage: parent(a)
Finite Field in a of size 19^2
sage: b=a**20;p=b.charpoly("x");p
x^2 + 15*x + 4
sage: factor(p)
(x + 17)^2
sage: b.minpoly('x')
x + 17

multiplicative_order()

Return the multiplicative order of this field element.

norm()

Return the norm of self down to the prime subfield.

This is the product of the Galois conjugates of self.

EXAMPLES:

sage: S.<b> = GF(5^2); S
Finite Field in b of size 5^2
sage: b.norm()
2
sage: b.charpoly('t')
t^2 + 4*t + 2

Next we consider a cubic extension:

sage: S.<a> = GF(5^3); S
Finite Field in a of size 5^3
sage: a.norm()
2
sage: a.charpoly('t')
t^3 + 3*t + 3
sage: a * a^5 * (a^25)
2            

nth_root(n, extend=False, all=False)

Returns an nth root of self.

INPUT:

• n - integer >= 1 (must fit in C int type)
• extend - bool (default: True); if True, return an nth root in an extension ring, if necessary. Otherwise, raise a ValueError if the root is not in the base ring. Warning: this option is not implemented!
• all - bool (default: False); if True, return all nth roots of self, instead of just one.

OUTPUT:

If self has an nth root, returns one (if all == False) or a list of all of them (if all == True). Otherwise, raises a ValueError (if extend = False) or a NotImplementedError (if extend = True).

Warning

The ‘extend’ option is not implemented (yet).

AUTHOR:

• David Roe (2007-10-3)

pth_power(k=1)

Return the 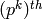power of self, where is the characteristic of the field.

INPUT:

• k - integer (default: 1, must fit in C int type)

Note that if is negative, then this computes the appropriate root.

EXAMPLES:

sage: F.<a> = GF(29^2)
sage: z = a^2 + 5*a + 1
sage: z.pth_power()
19*a + 20
sage: z.pth_power(10)
10*a + 28
sage: z.pth_power(-10) == z
True
sage: F.<b> = GF(2^12)
sage: y = b^3 + b + 1
sage: y == (y.pth_power(-3))^(2^3)
True
sage: y.pth_power(2)
b^7 + b^6 + b^5 + b^4 + b^3 + b

pth_root(k=1)

Return the 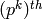root of self, where is the characteristic of the field.

INPUT:

• k - integer (default: 1, must fit in C int type)

Note that if is negative, then this computes the appropriate power.

EXAMPLES:

sage: F.<b> = GF(2^12)
sage: y = b^3 + b + 1
sage: y == (y.pth_root(3))^(2^3)
True
sage: y.pth_root(2)
b^11 + b^10 + b^9 + b^7 + b^5 + b^4 + b^2 + b

trace()

Return the trace of this element, which is the sum of the Galois conjugates.

EXAMPLES:

sage: S.<a> = GF(5^3); S
Finite Field in a of size 5^3
sage: a.trace()
0
sage: a.charpoly('t')
t^3 + 3*t + 3
sage: a + a^5 + a^25
0
sage: z = a^2 + a + 1
sage: z.trace()
2
sage: z.charpoly('t')
t^3 + 3*t^2 + 2*t + 2
sage: z + z^5 + z^25
2        

vector(reverse=False)

See _vector_().

EXAMPLE:

sage: k.<a> = GF(2^16)
sage: e = a^2 + 1
sage: e.vector() # random-ish error message
doctest:1: DeprecationWarning:The function vector is replaced by _vector_.
(1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)

sage.rings.finite_rings.element_base.is_FiniteFieldElement(x)

Returns if x is a finite field element.

EXAMPLE:

sage: from sage.rings.finite_rings.element_ext_pari import is_FiniteFieldElement
sage: is_FiniteFieldElement(1)
False
sage: is_FiniteFieldElement(IntegerRing())
False
sage: is_FiniteFieldElement(GF(5)(2))
True