Lines, Frames, Spheres, Points, Dots, and Text

class sage.plot.plot3d.shapes2.Line(points, thickness=5, corner_cutoff=0.5, arrow_head=False, **kwds)

Bases: sage.plot.plot3d.base.PrimitiveObject

Draw a 3d line joining a sequence of points.

This line has a fixed diameter unaffected by transformations and zooming. It may be smoothed if corner_cutoff < 1.

INPUT:

• points - list of points to pass through
• thickness - diameter of the line
• corner_cutoff - threshold for smoothing (see the corners() method) this is the minimum cosine between adjacent segments to smooth
• arrow_head - if True make this curve into an arrow

EXAMPLES:

sage: from sage.plot.plot3d.shapes2 import Line
sage: Line([(i*math.sin(i), i*math.cos(i), i/3) for i in range(30)], arrow_head=True)

Smooth angles less than 90 degrees:

sage: Line([(0,0,0),(1,0,0),(2,1,0),(0,1,0)], corner_cutoff=0)

bounding_box()

corners(corner_cutoff=None, max_len=None)

Figures out where the curve turns too sharply to pretend it’s smooth.

INPUT: Maximum cosine of angle between adjacent line segments before adding a corner

OUTPUT: List of points at which to start a new line. This always includes the first point, and never the last.

EXAMPLES:

Every point:

sage: from sage.plot.plot3d.shapes2 import Line
sage: Line([(0,0,0),(1,0,0),(2,1,0),(0,1,0)], corner_cutoff=1).corners()
[(0, 0, 0), (1, 0, 0), (2, 1, 0)]

Greater than 90 degrees:

sage: Line([(0,0,0),(1,0,0),(2,1,0),(0,1,0)], corner_cutoff=0).corners()
[(0, 0, 0), (2, 1, 0)]

No corners:

sage: Line([(0,0,0),(1,0,0),(2,1,0),(0,1,0)], corner_cutoff=-1).corners()
(0, 0, 0)

An intermediate value:

sage: Line([(0,0,0),(1,0,0),(2,1,0),(0,1,0)], corner_cutoff=.5).corners()
[(0, 0, 0), (2, 1, 0)]

jmol_repr(render_params)

obj_repr(render_params)

tachyon_repr(render_params)

class sage.plot.plot3d.shapes2.Point(center, size=1, **kwds)

Bases: sage.plot.plot3d.base.PrimitiveObject

Create a position in 3-space, represented by a sphere of fixed size.

INPUT:

• center - point (3-tuple)
• size - (default: 1)

bounding_box()

jmol_repr(render_params)

obj_repr(render_params)

tachyon_repr(render_params)

sage.plot.plot3d.shapes2.avg(a, b)

sage.plot.plot3d.shapes2.bezier3d(*args, **kwds)

Draws a 3-dimensional bezier path. Input is similar to bezier_path, but each point in the path and each control point is required to have 3 coordinates.

INPUT:

• path - a list of curves, which each is a list of points. See further

  detail below.

• thickness - (default: 2)

• color - a word that describes a color

• opacity - (default: 1) if less than 1 then is transparent

• aspect_ratio - (default:[1,1,1])

The path is a list of curves, and each curve is a list of points. Each point is a tuple (x,y,z).

The first curve contains the endpoints as the first and last point in the list. All other curves assume a starting point given by the last entry in the preceding list, and take the last point in the list as their opposite endpoint. A curve can have 0, 1 or 2 control points listed between the endpoints. In the input example for path below, the first and second curves have 2 control points, the third has one, and the fourth has no control points:

path = [[p1, c1, c2, p2], [c3, c4, p3], [c5, p4], [p5], ...]

In the case of no control points, a straight line will be drawn between the two endpoints. If one control point is supplied, then the curve at each of the endpoints will be tangent to the line from that endpoint to the control point. Similarly, in the case of two control points, at each endpoint the curve will be tangent to the line connecting that endpoint with the control point immediately after or immediately preceding it in the list.

So in our example above, the curve between p1 and p2 is tangent to the line through p1 and c1 at p1, and tangent to the line through p2 and c2 at p2. Similarly, the curve between p2 and p3 is tangent to line(p2,c3) at p2 and tangent to line(p3,c4) at p3. Curve(p3,p4) is tangent to line(p3,c5) at p3 and tangent to line(p4,c5) at p4. Curve(p4,p5) is a straight line.

EXAMPLES:

sage: path = [[(0,0,0),(.5,.1,.2),(.75,3,-1),(1,1,0)],[(.5,1,.2),(1,.5,0)],[(.7,.2,.5)]] sage: b = bezier3d(path, color=’green’) sage: b

To construct a simple curve, create a list containing a single list:

sage: path = [[(0,0,0),(1,0,0),(0,1,0),(0,1,1)]] sage: curve = bezier3d(path, thickness=5, color=’blue’) sage: curve

sage.plot.plot3d.shapes2.dot((x0, y0, z0), (x1, y1, z1))

sage.plot.plot3d.shapes2.frame3d(lower_left, upper_right, **kwds)

Draw a frame in 3d.

sage.plot.plot3d.shapes2.frame_labels(lower_left, upper_right, label_lower_left, label_upper_right, eps=1, **kwds)

sage.plot.plot3d.shapes2.line3d(points, thickness=1, radius=None, arrow_head=False, **kwds)

Draw a 3d line joining a sequence of points.

One may specify either a thickness or radius. If a thickness is specified, this line will have a constant diameter regardless of scaling and zooming. If a radius is specified, it will behave as a series of cylinders.

INPUT:

• points - a list of at least 2 points
• thickness - (default: 1)
• radius - (default: None)
• arrow_head - (default: False)
• color - a word that describes a color
• rgbcolor - (r,g,b) with r, g, b between 0 and 1 that describes a color
• opacity - (default: 1) if less than 1 then is transparent

EXAMPLES:

A line in 3-space:

sage: line3d([(1,2,3), (1,0,-2), (3,1,4), (2,1,-2)])

The same line but red:

sage: line3d([(1,2,3), (1,0,-2), (3,1,4), (2,1,-2)], color='red')

A transparent thick green line and a little blue line:

sage: line3d([(0,0,0), (1,1,1), (1,0,2)], opacity=0.5, radius=0.1, \
             color='green') + line3d([(0,1,0), (1,0,2)])

A Dodecahedral complex of 5 tetrahedrons (a more elaborate examples from Peter Jipsen):

sage: def tetra(col): 
...       return line3d([(0,0,1), (2*sqrt(2.)/3,0,-1./3), (-sqrt(2.)/3, sqrt(6.)/3,-1./3),\
...              (-sqrt(2.)/3,-sqrt(6.)/3,-1./3), (0,0,1), (-sqrt(2.)/3, sqrt(6.)/3,-1./3),\
...              (-sqrt(2.)/3,-sqrt(6.)/3,-1./3), (2*sqrt(2.)/3,0,-1./3)],\
...              color=col, thickness=10, aspect_ratio=[1,1,1])
...
sage: v  = (sqrt(5.)/2-5/6, 5/6*sqrt(3.)-sqrt(15.)/2, sqrt(5.)/3)
sage: t  = acos(sqrt(5.)/3)/2
sage: t1 = tetra('blue').rotateZ(t)
sage: t2 = tetra('red').rotateZ(t).rotate(v,2*pi/5)
sage: t3 = tetra('green').rotateZ(t).rotate(v,4*pi/5)
sage: t4 = tetra('yellow').rotateZ(t).rotate(v,6*pi/5)
sage: t5 = tetra('orange').rotateZ(t).rotate(v,8*pi/5)
sage: show(t1+t2+t3+t4+t5, frame=False)

TESTS:

Copies are made of the input list, so the input list does not change:

sage: mypoints = [vector([1,2,3]), vector([4,5,6])]
sage: type(mypoints[0])
<type 'sage.modules.vector_integer_dense.Vector_integer_dense'>
sage: L = line3d(mypoints)
sage: type(mypoints[0])
<type 'sage.modules.vector_integer_dense.Vector_integer_dense'>

sage.plot.plot3d.shapes2.point3d(v, size=5, **kwds)

Plot a point or list of points in 3d space.

INPUT:

• v - a point or list of points
• size - (default: 5) size of the point (or points)
• color - a word that describes a color
• rgbcolor - (r,g,b) with r, g, b between 0 and 1 that describes a color
• opacity - (default: 1) if less than 1 then is transparent

EXAMPLES:

sage: sum([point3d((i,i^2,i^3), size=5) for i in range(10)])

We check to make sure this works with vectors.

sage: pl = point3d([vector(ZZ,(1, 0, 0)), vector(ZZ,(0, 1, 0)), (-1, -1, 0)])

sage.plot.plot3d.shapes2.polygon3d(*args, **kwds)

Draw a polygon in 3d.

INPUT:

• points - the vertices of the polygon

Type polygon3d.options for a dictionary of the default options for polygons. You can change this to change the defaults for all future polygons. Use polygon3d.reset() to reset to the default options.

EXAMPLES:

A simple triangle:

sage: polygon3d([[0,0,0], [1,2,3], [3,0,0]])

Some modern art – a random polygon:

sage: v = [(randrange(-5,5), randrange(-5,5), randrange(-5, 5)) for _ in range(10)]
sage: polygon3d(v)

A bent transparent green triangle:

sage: polygon3d([[1, 2, 3], [0,1,0], [1,0,1], [3,0,0]], color=(0,1,0), alpha=0.7)

sage.plot.plot3d.shapes2.ruler(start, end, ticks=4, sub_ticks=4, absolute=False, snap=False, **kwds)

sage.plot.plot3d.shapes2.ruler_frame(lower_left, upper_right, ticks=4, sub_ticks=4, **kwds)

sage.plot.plot3d.shapes2.sphere(center=(0, 0, 0), size=1, **kwds)

Return a plot of a sphere of radius size centered at .

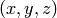INPUT:

• (x,y,z) - center (default: (0,0,0)
• size - the radius (default: 1)

EXAMPLES: A simple sphere:

sage: sphere()

Two spheres touching:

sage: sphere(center=(-1,0,0)) + sphere(center=(1,0,0), aspect_ratio=[1,1,1])

Spheres of radii 1 and 2 one stuck into the other:

sage: sphere(color='orange') + sphere(color=(0,0,0.3), \
             center=(0,0,-2),size=2,opacity=0.9)    

We draw a transparent sphere on a saddle.

sage: u,v = var('u v')
sage: saddle = plot3d(u^2 - v^2, (u,-2,2), (v,-2,2))
sage: sphere((0,0,1), color='red', opacity=0.5, aspect_ratio=[1,1,1]) + saddle

TESTS:

sage: T = sage.plot.plot3d.texture.Texture('red')
sage: S = sphere(texture=T)
sage: T in S.texture_set()
True

sage.plot.plot3d.shapes2.text3d(txt, (x, y, z), **kwds)

Display 3d text.

INPUT:

• txt - some text
• (x,y,z) - position
• **kwds - standard 3d graphics options

Note

There is no way to change the font size or opacity yet.

EXAMPLES: We write the word Sage in red at position (1,2,3):

sage: text3d("Sage", (1,2,3), color=(0.5,0,0))

We draw a multicolor spiral of numbers:

sage: sum([text3d('%.1f'%n, (cos(n),sin(n),n), color=(n/2,1-n/2,0)) \
            for n in [0,0.2,..,8]])

Another example

sage: text3d("Sage is really neat!!",(2,12,1))

And in 3d in two places:

sage: text3d("Sage is...",(2,12,1), rgbcolor=(1,0,0)) + text3d("quite powerful!!",(4,10,0), rgbcolor=(0,0,1))

sage.plot.plot3d.shapes2.validate_frame_size(size)