Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- 3D Graphics »

EXAMPLES: The five platonic solids in a row;
sage: G = tetrahedron((0,-3.5,0), color='blue') + cube((0,-2,0),color=(.25,0,.5)) +\
octahedron(color='red') + dodecahedron((0,2,0), color='orange') +\
icosahedron(center=(0,4,0), color='yellow')
sage: G.show(aspect_ratio=[1,1,1])
All the platonic solids in the same place:
sage: G = tetrahedron(color='blue',opacity=0.7) + \
cube(color=(.25,0,.5), opacity=0.7) +\
octahedron(color='red', opacity=0.7) + \
dodecahedron(color='orange', opacity=0.7) + icosahedron(opacity=0.7)
sage: G.show(aspect_ratio=[1,1,1])
Display nice faces only:
sage: icosahedron().stickers(['red','blue'], .075, .1)
AUTHORS:
A 3D cube centered at the origin with default side lengths 1.
INPUT:
EXAMPLES:
A simple cube:
sage: cube()
A red cube:
sage: cube(color="red")
A transparent grey cube that contains a red cube:
sage: cube(opacity=0.8, color='grey') + cube(size=3/4)
A transparent colored cube:
sage: cube(color=['red', 'green', 'blue'], opacity=0.5)
A bunch of random cubes:
sage: v = [(random(), random(), random()) for _ in [1..30]]
sage: sum([cube((10*a,10*b,10*c), size=random()/3, color=(a,b,c)) for a,b,c in v])
Non-square cubes (boxes):
sage: cube(aspect_ratio=[1,1,1]).scale([1,2,3])
sage: cube(color=['red', 'blue', 'green'],aspect_ratio=[1,1,1]).scale([1,2,3])
And one that is colored:
sage: cube(color=['red', 'blue', 'green', 'black', 'white', 'orange'], aspect_ratio=[1,1,1]).scale([1,2,3])
A nice translucent color cube with a frame:
sage: c = cube(color=['red', 'blue', 'green'], frame=False, frame_thickness=2, frame_color='brown', opacity=0.8)
sage: c
A raytraced color cube with frame and transparency:
sage: c.show(viewer='tachyon')
AUTHORS:
A dodecahedron.
INPUT:
EXAMPLES: A plain Dodecahedron:
sage: dodecahedron()
A translucent dodecahedron that contains a black sphere:
sage: dodecahedron(color='orange', opacity=0.8) + \
sphere(size=0.5, color='black')
CONSTRUCTION: This is how we construct a dodecahedron. We let one
point be 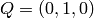 .
.
Now there are three points spaced equally on a circle around the
north pole. The other requirement is that the angle between them be
the angle of a pentagon, namely 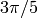 . This is enough to
determine them. Placing one on the
. This is enough to
determine them. Placing one on the 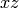 -plane we have.
-plane we have.
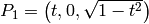
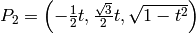
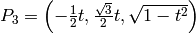
Solving
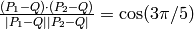 we get
we get 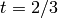 .
.
Now we have 6 points 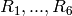 to close the three
top pentagons. These can be found by mirroring
to close the three
top pentagons. These can be found by mirroring 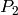 and
and
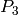 by the
by the 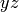 -plane and rotating around the
-plane and rotating around the
 -axis by the angle
-axis by the angle 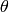 from
from 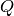 to
to
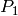 . Note that
. Note that 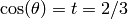 and so
and so
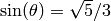 . Rotation gives us the other
four.
. Rotation gives us the other
four.
Now we reflect through the origin for the bottom half.
AUTHORS:
An icosahedron.
INPUT:
EXAMPLES:
sage: icosahedron()
Two icosahedrons at different positions of different sizes.
sage: icosahedron((-1/2,0,1), color='orange') + \
icosahedron((2,0,1), size=1/2, aspect_ratio=[1,1,1])
Return an octahedron.
INPUT:
EXAMPLES:
sage: octahedron((1,4,3), color='orange') + \
octahedron((0,2,1), size=2, opacity=0.6)
A 3d tetrahedron.
INPUT:
EXAMPLES: A default colored tetrahedron at the origin:
sage: tetrahedron()
A transparent green tetrahedron in front of a solid red one:
sage: tetrahedron(opacity=0.8, color='green') + tetrahedron((-2,1,0),color='red')
A translucent tetrahedron sharing space with a sphere:
sage: tetrahedron(color='yellow',opacity=0.7) + sphere(r=.5, color='red')
A big tetrahedron:
sage: tetrahedron(size=10)
A wide tetrahedron:
sage: tetrahedron(aspect_ratio=[1,1,1]).scale((4,4,1))
A red and blue tetrahedron touching noses:
sage: tetrahedron(color='red') + tetrahedron((0,0,-2)).scale([1,1,-1])
A Dodecahedral complex of 5 tetrahedrons (a more elaborate examples from Peter Jipsen):
sage: v=(sqrt(5.)/2-5/6, 5/6*sqrt(3.)-sqrt(15.)/2, sqrt(5.)/3)
sage: t=acos(sqrt(5.)/3)/2
sage: t1=tetrahedron(aspect_ratio=(1,1,1), opacity=0.5).rotateZ(t)
sage: t2=tetrahedron(color='red', opacity=0.5).rotateZ(t).rotate(v,2*pi/5)
sage: t3=tetrahedron(color='green', opacity=0.5).rotateZ(t).rotate(v,4*pi/5)
sage: t4=tetrahedron(color='yellow', opacity=0.5).rotateZ(t).rotate(v,6*pi/5)
sage: t5=tetrahedron(color='orange', opacity=0.5).rotateZ(t).rotate(v,8*pi/5)
sage: show(t1+t2+t3+t4+t5, frame=False, zoom=1.3)
AUTHORS: