Base classes for 3D Graphics objects and plotting.¶

AUTHORS:

Robert Bradshaw (2007-02): initial version
Robert Bradshaw (2007-08): Cythonization, much optimization
William Stein (2008)

TODO: - finish integrating tachyon - good default lights, camera

class sage.plot.plot3d.base.BoundingSphere¶

Bases: sage.structure.sage_object.SageObject

A bounding sphere is like a bounding box, but is simpler to deal with and behaves better under rotations.

transform(T)¶

Returns the bounding sphere of this sphere acted on by T. This always returns a new sphere, even if the resulting object is an ellipsoid.

EXAMPLES:

sage: from sage.plot.plot3d.transform import Transformation
sage: from sage.plot.plot3d.base import BoundingSphere
sage: BoundingSphere((0,0,0), 10).transform(Transformation(trans=(1,2,3)))
Center (1.0, 2.0, 3.0) radius 10.0
sage: BoundingSphere((0,0,0), 10).transform(Transformation(scale=(1/2, 1, 2)))
Center (0.0, 0.0, 0.0) radius 20.0
sage: BoundingSphere((0,0,3), 10).transform(Transformation(scale=(2, 2, 2)))
Center (0.0, 0.0, 6.0) radius 20.0

class sage.plot.plot3d.base.Graphics3d¶

Bases: sage.structure.sage_object.SageObject

This is the baseclass for all 3d graphics objects.

aspect_ratio(v=None)¶

Sets or gets the preferred aspect ratio of self.

EXAMPLES:

sage: D = dodecahedron()
sage: D.aspect_ratio()
[1.0, 1.0, 1.0]
sage: D.aspect_ratio([1,2,3])
sage: D.aspect_ratio()
[1.0, 2.0, 3.0]
sage: D.aspect_ratio(1)
sage: D.aspect_ratio()
[1.0, 1.0, 1.0]

bounding_box()¶

Returns the lower and upper corners of a 3d bounding box for self. This is used for rendering and self should fit entirely within this box.

Specifically, the first point returned should have x, y, and z coordinates should be the respective infimum over all points in self, and the second point is the supremum.

The default return value is simply the box containing the origin.

EXAMPLES:

sage: sphere((1,1,1), 2).bounding_box()
((-1.0, -1.0, -1.0), (3.0, 3.0, 3.0))
sage: G = line3d([(1, 2, 3), (-1,-2,-3)])
sage: G.bounding_box()
((-1.0, -2.0, -3.0), (1.0, 2.0, 3.0))

default_render_params()¶

Returns an instance of RenderParams suitable for plotting this object.

EXAMPLES:

sage: type(dodecahedron().default_render_params())
<class 'sage.plot.plot3d.base.RenderParams'>

export_jmol(filename='jmol_shape.jmol', force_reload=False, zoom=100, spin=False, background=(1, 1, 1), stereo=False, mesh=False, dots=False, perspective_depth=True, orientation=(-764, -346, -545, 76.390000000000001), **ignored_kwds)¶

A jmol scene consists of a script which refers to external files. Fortunately, we are able to put all of them in a single zip archive, which is the output of this call.

EXAMPLES:

sage: out_file = sage.misc.misc.tmp_filename() + ".jmol"
sage: G = sphere((1, 2, 3), 5) + cube() + sage.plot.plot3d.shapes.Text("hi")
sage: G.export_jmol(out_file)
sage: import zipfile
sage: z = zipfile.ZipFile(out_file)
sage: z.namelist()
['obj_...pmesh', 'SCRIPT']

sage: print z.read('SCRIPT')
data "model list"
2
empty
Xx 0 0 0
Xx 5.5 5.5 5.5
end "model list"; show data
select *
wireframe off; spacefill off
set labelOffset 0 0
background [255,255,255]
spin OFF
moveto 0 -764 -346 -545 76.39
centerAt absolute {0 0 0}
zoom 100
frank OFF
set perspectivedepth ON
isosurface sphere_1  center {1.0 2.0 3.0} sphere 5.0
color isosurface  [102,102,255]
pmesh obj_... "obj_...pmesh"
color pmesh  [102,102,255]
select atomno = 1
color atom  [102,102,255]
label "hi"

sage: print z.read(z.namelist()[0])
24
0.5 0.5 0.5
-0.5 0.5 0.5
...
-0.5 -0.5 -0.5
6
5
0
1
...

flatten()¶

Try to reduce the depth of the scene tree by consolidating groups and transformations.

The generic Graphics3d object can’t be made flatter.

EXAMPLES:

sage: G = sage.plot.plot3d.base.Graphics3d()
sage: G.flatten() is G
True

frame_aspect_ratio(v=None)¶

Sets or gets the preferred frame aspect ratio of self.

EXAMPLES:

sage: D = dodecahedron()
sage: D.frame_aspect_ratio()
[1.0, 1.0, 1.0]
sage: D.frame_aspect_ratio([2,2,1])
sage: D.frame_aspect_ratio()
[2.0, 2.0, 1.0]
sage: D.frame_aspect_ratio(1)
sage: D.frame_aspect_ratio()
[1.0, 1.0, 1.0]

jmol_repr(render_params)¶

A (possibly nested) list of strings which will be concatenated and used by jmol to render self. (Nested lists of strings are used because otherwise all the intermediate concatenations can kill performance). This may refer to several remove files, which are stored in render_parames.output_archive.

EXAMPLES:

sage: G = sage.plot.plot3d.base.Graphics3d()
sage: G.jmol_repr(G.default_render_params())
[]
sage: G = sphere((1, 2, 3))
sage: G.jmol_repr(G.default_render_params())
[['isosurface sphere_1  center {1.0 2.0 3.0} sphere 1.0\ncolor isosurface  [102,102,255]']]

json_repr(render_params)¶

A (possibly nested) list of strings. Each entry is formatted as JSON, so that a JavaScript client could eval it and get an object. Each object has fields to encapsulate the faces and vertices of self. This representation is intended to be consumed by the canvas3d viewer backend.

EXAMPLES:

sage: G = sage.plot.plot3d.base.Graphics3d()
sage: G.json_repr(G.default_render_params())
[]

mtl_str()¶

Returns the contents of a .mtl file, to be used to provide coloring information for an .obj file.

EXAMPLES::: sage: G = tetrahedron(color=’red’) + tetrahedron(color=’yellow’, opacity=0.5) sage: print G.mtl_str() newmtl ... Ka 0.5 5e-06 5e-06 Kd 1.0 1e-05 1e-05 Ks 0.0 0.0 0.0 illum 1 Ns 1 d 1 newmtl ... Ka 0.5 0.5 5e-06 Kd 1.0 1.0 1e-05 Ks 0.0 0.0 0.0 illum 1 Ns 1 d 0.500000000000000

obj()¶

An .obj scene file (as a string) containing the this object. A .mtl file of the same name must also be produced for coloring.

EXAMPLES:

sage: from sage.plot.plot3d.shapes import ColorCube
sage: print ColorCube(1, ['red', 'yellow', 'blue']).obj()
g obj_1
usemtl ...
v 1 1 1
v -1 1 1
v -1 -1 1
v 1 -1 1
f 1 2 3 4
...
g obj_6
usemtl ...
v -1 -1 1
v -1 1 1
v -1 1 -1
v -1 -1 -1
f 21 22 23 24

obj_repr(render_params)¶

A (possibly nested) list of strings which will be concatenated and used to construct an .obj file of self. (Nested lists of strings are used because otherwise all the intermediate concatenations can kill performance). This may include a reference to color information which is stored elsewhere.

EXAMPLES:

sage: G = sage.plot.plot3d.base.Graphics3d()
sage: G.obj_repr(G.default_render_params())
[]
sage: G = cube()
sage: G.obj_repr(G.default_render_params())
['g obj_1',
 'usemtl ...',
 ['v 0.5 0.5 0.5',
  'v -0.5 0.5 0.5',
  'v -0.5 -0.5 0.5',
  'v 0.5 -0.5 0.5',
  'v 0.5 0.5 -0.5',
  'v -0.5 0.5 -0.5',
  'v 0.5 -0.5 -0.5',
  'v -0.5 -0.5 -0.5'],
 ['f 1 2 3 4',
  'f 1 5 6 2',
  'f 1 4 7 5',
  'f 6 5 7 8',
  'f 7 4 3 8',
  'f 3 2 6 8'],
 []]

rotate(v, theta)¶

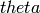Returns self rotated about the vector $v$ by $theta$ radians.

EXAMPLES:

sage: from sage.plot.plot3d.shapes import Cone
sage: v = (1,2,3)
sage: G = arrow3d((0, 0, 0), v)
sage: G += Cone(1/5, 1).translate((0, 0, 2))
sage: C = Cone(1/5, 1, opacity=.25).translate((0, 0, 2))
sage: G += sum(C.rotate(v, pi*t/4) for t in [1..7])
sage: G.show(aspect_ratio=1)

sage: from sage.plot.plot3d.shapes import Box
sage: Box(1/3, 1/5, 1/7).rotate((1, 1, 1), pi/3).show(aspect_ratio=1)

rotateX(theta)¶

Returns self rotated about the $x$ -axis by the given angle.

EXAMPLES:

sage: from sage.plot.plot3d.shapes import Cone
sage: G = Cone(1/5, 1) + Cone(1/5, 1, opacity=.25).rotateX(pi/2)
sage: G.show(aspect_ratio=1)

rotateY(theta)¶

Returns self rotated about the $y$ -axis by the given angle.

EXAMPLES:

sage: from sage.plot.plot3d.shapes import Cone
sage: G = Cone(1/5, 1) + Cone(1/5, 1, opacity=.25).rotateY(pi/3)
sage: G.show(aspect_ratio=1)

rotateZ(theta)¶

Returns self rotated about the $z$ -axis by the given angle.

EXAMPLES:

sage: from sage.plot.plot3d.shapes import Box
sage: G = Box(1/2, 1/3, 1/5) + Box(1/2, 1/3, 1/5, opacity=.25).rotateZ(pi/5)
sage: G.show(aspect_ratio=1)

save(filename, **kwds)¶

Save the graphic to an image file (of type: PNG, BMP, GIF, PPM, or TIFF) rendered using Tachyon, or pickle it (stored as an SOBJ so you can load it later) depending on the file extension you give the filename.

INPUT:

filename - Specify where to save the image or object.
**kwds - When specifying an image file to be rendered by Tachyon, any of the viewing options accepted by show() are valid as keyword arguments to this function and they will behave in the same way. Accepted keywords include: viewer, verbosity, figsize, aspect_ratio, frame_aspect_ratio, zoom, frame, and axes. Default values are provided.

EXAMPLES:

sage: f = tmp_filename() + '.png'
sage: G = sphere()
sage: G.save(f)

We demonstrate using keyword arguments to control the appearance of the output image:

sage: G.save(f, zoom=2, figsize=[5, 10])

But some extra parameters don’t make since (like viewer, since rendering is done using Tachyon only). They will be ignored:

sage: G.save(f, viewer='jmol') # Looks the same

Since Tachyon only outputs PNG images, PIL will be used to convert to alternate formats:

sage: cube().save(tmp_filename() + '.gif')

scale(*x)¶

Returns self scaled in the x, y, and z directions.

EXAMPLES:

sage: G = dodecahedron() + dodecahedron(opacity=.5).scale(2)
sage: G.show(aspect_ratio=1)
sage: G = icosahedron() + icosahedron(opacity=.5).scale([1, 1/2, 2])
sage: G.show(aspect_ratio=1)

TESTS:

sage: G = sphere((0, 0, 0), 1)
sage: G.scale(2)
sage: G.scale(1, 2, 1/2).show(aspect_ratio=1)
sage: G.scale(2).bounding_box()
((-2.0, -2.0, -2.0), (2.0, 2.0, 2.0))

show(**kwds)¶

INPUT:

viewer - string (default: ‘jmol’), how to view the plot
- ‘jmol’: Interactive 3D viewer using Java
- ‘tachyon’: Ray tracer generates a static PNG image
- ‘java3d’: Interactive OpenGL based 3D
- ‘canvas3d’: Web-based 3D viewer powered by JavaScript and <canvas> (notebook only)
filename - string (default: a temp file); file to save the image to
verbosity - display information about rendering the figure
figsize - (default: 5); x or pair [x,y] for numbers, e.g., [5,5]; controls the size of the output figure. E.g., with Tachyon the number of pixels in each direction is 100 times figsize[0]. This is ignored for the jmol embedded renderer.
aspect_ratio - (default: “automatic”) - aspect ratio of the coordinate system itself. Give [1,1,1] to make spheres look round.
frame_aspect_ratio - (default: “automatic”) aspect ratio of frame that contains the 3d scene.
zoom - (default: 1) how zoomed in
frame - (default: True) if True, draw a bounding frame with labels
axes - (default: False) if True, draw coordinate axes
**kwds - other options, which make sense for particular rendering engines

CHANGING DEFAULTS: Defaults can be uniformly changed by importing a dictionary and changing it. For example, here we change the default so images display without a frame instead of with one:

sage: from sage.plot.plot3d.base import SHOW_DEFAULTS
sage: SHOW_DEFAULTS['frame'] = False

This sphere will not have a frame around it:

sage: sphere((0,0,0))

We change the default back:

sage: SHOW_DEFAULTS['frame'] = True

Now this sphere is enclosed in a frame:

sage: sphere((0,0,0))

EXAMPLES: We illustrate use of the aspect_ratio option:

sage: x, y = var('x,y')
sage: p = plot3d(2*sin(x*y), (x, -pi, pi), (y, -pi, pi))
sage: p.show(aspect_ratio=[1,1,1])

This looks flattened, but filled with the plot:

sage: p.show(frame_aspect_ratio=[1,1,1/16])

This looks flattened, but the plot is square and smaller:

sage: p.show(aspect_ratio=[1,1,1], frame_aspect_ratio=[1,1,1/8])

We use the ‘canvas3d’ backend from inside the notebook to get a view of the plot rendered inline using HTML canvas:

sage: p.show(viewer='canvas3d')

tachyon()¶

An tachyon input file (as a string) containing the this object.

EXAMPLES:

sage: print sphere((1, 2, 3), 5, color='yellow').tachyon()
begin_scene
resolution 400 400
         camera
        ...
      plane
        center -2000 -1000 -500
        normal 2.3 2.4 2.0
        TEXTURE
            AMBIENT 1.0 DIFFUSE 1.0 SPECULAR 1.0 OPACITY 1.0
            COLOR 1.0 1.0 1.0
            TEXFUNC 0
    Texdef texture...
  Ambient 0.333333333333 Diffuse 0.666666666667 Specular 0.0 Opacity 1
   Color 1.0 1.0 0.0
   TexFunc 0
    Sphere center 1.0 -2.0 3.0 Rad 5.0 texture...
end_scene

sage: G = icosahedron(color='red') + sphere((1,2,3), 0.5, color='yellow')
sage: G.show(viewer='tachyon', frame=false)
sage: print G.tachyon()
begin_scene
...
Texdef texture...
  Ambient 0.333333333333 Diffuse 0.666666666667 Specular 0.0 Opacity 1
   Color 1.0 0.0 0.0
   TexFunc 0
TRI V0 ...
Sphere center 1.0 -2.0 3.0 Rad 0.5 texture...
end_scene

tachyon_repr(render_params)¶

A (possibly nested) list of strings which will be concatenated and used by tachyon to render self. (Nested lists of strings are used because otherwise all the intermediate concatenations can kill performance). This may include a reference to color information which is stored elsewhere.

EXAMPLES::: sage: G = sage.plot.plot3d.base.Graphics3d() sage: G.tachyon_repr(G.default_render_params()) [] sage: G = sphere((1, 2, 3)) sage: G.tachyon_repr(G.default_render_params()) [‘Sphere center 1.0 2.0 3.0 Rad 1.0 texture...’]

testing_render_params()¶

Returns an instance of RenderParams suitable for testing this object. In particular, it opens up ‘/dev/null’ as an auxiliary zip file for jmol.

EXAMPLES:

sage: type(dodecahedron().testing_render_params())
<class 'sage.plot.plot3d.base.RenderParams'>

texture¶

texture_set()¶

Often the textures of a 3d file format are kept separate from the objects themselves. This function returns the set of textures used, so they can be defined in a preamble or separate file.

EXAMPLES:

sage: sage.plot.plot3d.base.Graphics3d().texture_set()
set([])

sage: G = tetrahedron(color='red') + tetrahedron(color='yellow') + tetrahedron(color='red', opacity=0.5)
sage: [t for t in G.texture_set() if t.color == colors.red] # we should have two red textures
[Texture(texture..., red, ff0000), Texture(texture..., red, ff0000)]
sage: [t for t in G.texture_set() if t.color == colors.yellow] # ...and one yellow
[Texture(texture..., yellow, ffff00)]

transform(**kwds)¶

Apply a transformation to self, where the inputs are passed onto a TransformGroup object. Mostly for internal use; see the translate, scale, and rotate methods for more details.

EXAMPLES:

sage: sphere((0,0,0), 1).transform(trans=(1, 0, 0), scale=(2,3,4)).bounding_box()
((-1.0, -3.0, -4.0), (3.0, 3.0, 4.0))

translate(*x)¶

Return self translated by the given vector (which can be given either as a 3-iterable or via positional arguments).

EXAMPLES:

sage: icosahedron() + sum(icosahedron(opacity=0.25).translate(2*n, 0, 0) for n in [1..4])
sage: icosahedron() + sum(icosahedron(opacity=0.25).translate([-2*n, n, n^2]) for n in [1..4])

TESTS:

sage: G = sphere((0, 0, 0), 1)
sage: G.bounding_box()
((-1.0, -1.0, -1.0), (1.0, 1.0, 1.0))
sage: G.translate(0, 0, 1).bounding_box()
((-1.0, -1.0, 0.0), (1.0, 1.0, 2.0))
sage: G.translate(-1, 5, 0).bounding_box()
((-2.0, 4.0, -1.0), (0.0, 6.0, 1.0))

viewpoint()¶

Returns the viewpoint of this plot. Currently only a stub for x3d.

EXAMPLES:

sage: type(dodecahedron().viewpoint())
<class 'sage.plot.plot3d.base.Viewpoint'>

x3d()¶

An x3d scene file (as a string) containing the this object.

EXAMPLES:

sage: print sphere((1, 2, 3), 5).x3d()
<X3D version='3.0' profile='Immersive' xmlns:xsd='http://www.w3.org/2001/XMLSchema-instance' xsd:noNamespaceSchemaLocation=' http://www.web3d.org/specifications/x3d-3.0.xsd '>
<head>
<meta name='title' content='sage3d'/>
</head>
<Scene>
<Viewpoint position='0 0 6'/>
<Transform translation='1 2 3'>
<Shape><Sphere radius='5.0'/><Appearance><Material diffuseColor='0.4 0.4 1.0' shininess='1' specularColor='0.0 0.0 0.0'/></Appearance></Shape>
</Transform>
</Scene>
</X3D>

sage: G = icosahedron() + sphere((0,0,0), 0.5, color='red')
sage: print G.x3d()
<X3D version='3.0' profile='Immersive' xmlns:xsd='http://www.w3.org/2001/XMLSchema-instance' xsd:noNamespaceSchemaLocation=' http://www.web3d.org/specifications/x3d-3.0.xsd '>
<head>
<meta name='title' content='sage3d'/>
</head>
<Scene>
<Viewpoint position='0 0 6'/>
<Shape>
<IndexedFaceSet coordIndex='...'>
  <Coordinate point='...'/>
</IndexedFaceSet>
<Appearance><Material diffuseColor='0.4 0.4 1.0' shininess='1' specularColor='0.0 0.0 0.0'/></Appearance></Shape>
<Transform translation='0 0 0'>
<Shape><Sphere radius='0.5'/><Appearance><Material diffuseColor='1.0 0.0 0.0' shininess='1' specularColor='0.0 0.0 0.0'/></Appearance></Shape>
</Transform>
</Scene>
</X3D>

class sage.plot.plot3d.base.Graphics3dGroup¶

Bases: sage.plot.plot3d.base.Graphics3d

This class represents a collection of 3d objects. Usually they are formed implicitly by summing.

bounding_box()¶

Box that contains the bounding boxes of all the objects that make up self.

EXAMPLES:

sage: A = sphere((0,0,0), 5)
sage: B = sphere((1, 5, 10), 1)
sage: A.bounding_box()
((-5.0, -5.0, -5.0), (5.0, 5.0, 5.0))
sage: B.bounding_box()
((0.0, 4.0, 9.0), (2.0, 6.0, 11.0))
sage: (A+B).bounding_box()
((-5.0, -5.0, -5.0), (5.0, 6.0, 11.0))
sage: (A+B).show(aspect_ratio=1, frame=True)

sage: sage.plot.plot3d.base.Graphics3dGroup([]).bounding_box()
((0.0, 0.0, 0.0), (0.0, 0.0, 0.0))

flatten()¶

Try to reduce the depth of the scene tree by consolidating groups and transformations.

EXAMPLES:

sage: G = sum([circle((0, 0), t) for t in [1..10]], sphere()); G
sage: G.flatten()
sage: len(G.all)
2
sage: len(G.flatten().all)
11

jmol_repr(render_params)¶

The jmol representation of a group is simply the concatenation of the representation of its objects.

EXAMPLES:

sage: G = sphere() + sphere((1,2,3))
sage: G.jmol_repr(G.default_render_params())
[[['isosurface sphere_1  center {0.0 0.0 0.0} sphere 1.0\ncolor isosurface  [102,102,255]']],
 [['isosurface sphere_2  center {1.0 2.0 3.0} sphere 1.0\ncolor isosurface  [102,102,255]']]]

json_repr(render_params)¶

The JSON representation of a group is simply the concatenation of the representations of its objects.

EXAMPLES:

sage: G = sphere() + sphere((1, 2, 3))
sage: G.json_repr(G.default_render_params())
[[["{vertices:..."]], [["{vertices:..."]]]

obj_repr(render_params)¶

The obj representation of a group is simply the concatenation of the representation of its objects.

EXAMPLES:

sage: G = tetrahedron() + tetrahedron().translate(10, 10, 10)
sage: G.obj_repr(G.default_render_params())
[['g obj_1',
  'usemtl ...',
  ['v 0 0 1',
   'v 0.942809 0 -0.333333',
   'v -0.471405 0.816497 -0.333333',
   'v -0.471405 -0.816497 -0.333333'],
  ['f 1 2 3', 'f 2 4 3', 'f 1 3 4', 'f 1 4 2'],
  []],
 [['g obj_2',
   'usemtl ...',
   ['v 10 10 11',
    'v 10.9428 10 9.66667',
    'v 9.5286 10.8165 9.66667',
    'v 9.5286 9.1835 9.66667'],
   ['f 5 6 7', 'f 6 8 7', 'f 5 7 8', 'f 5 8 6'],
   []]]]

set_texture(**kwds)¶

EXAMPLES:

sage: G = dodecahedron(color='red', opacity=.5) + icosahedron((3, 0, 0), color='blue')
sage: G
sage: G.set_texture(color='yellow')
sage: G

tachyon_repr(render_params)¶

The tachyon representation of a group is simply the concatenation of the representations of its objects.

EXAMPLES:

sage: G = sphere() + sphere((1,2,3))
sage: G.tachyon_repr(G.default_render_params())
[['Sphere center 0.0 0.0 0.0 Rad 1.0 texture...'],
 ['Sphere center 1.0 2.0 3.0 Rad 1.0 texture...']]

texture_set()¶

The texture set of a group is simply the union of the textures of all its objects.

EXAMPLES:

sage: G = sphere(color='red') + sphere(color='yellow')
sage: [t for t in G.texture_set() if t.color == colors.red] # one red texture
[Texture(texture..., red, ff0000)]
sage: [t for t in G.texture_set() if t.color == colors.yellow] # one yellow texture
[Texture(texture..., yellow, ffff00)] 

sage: T = sage.plot.plot3d.texture.Texture('blue'); T
Texture(texture..., blue, 0000ff)
sage: G = sphere(texture=T) + sphere((1, 1, 1), texture=T)
sage: len(G.texture_set())
1

transform(**kwds)¶

Transforming this entire group simply makes a transform group with the same contents.

EXAMPLES:

sage: G = dodecahedron(color='red', opacity=.5) + icosahedron(color='blue')
sage: G
sage: G.transform(scale=(2,1/2,1))
sage: G.transform(trans=(1,1,3))

x3d_str()¶

The x3d representation of a group is simply the concatenation of the representation of its objects.

EXAMPLES:

sage: G = sphere() + sphere((1,2,3))
sage: print G.x3d_str()
<Transform translation='0 0 0'>
<Shape><Sphere radius='1.0'/><Appearance><Material diffuseColor='0.4 0.4 1.0' shininess='1' specularColor='0.0 0.0 0.0'/></Appearance></Shape>
</Transform>
<Transform translation='1 2 3'>
<Shape><Sphere radius='1.0'/><Appearance><Material diffuseColor='0.4 0.4 1.0' shininess='1' specularColor='0.0 0.0 0.0'/></Appearance></Shape>
</Transform>

class sage.plot.plot3d.base.PrimitiveObject¶

Bases: sage.plot.plot3d.base.Graphics3d

This is the base class for the non-container 3d objects.

get_texture()¶

EXAMPLES:

sage: G = dodecahedron(color='red')
sage: G.get_texture()
Texture(texture..., red, ff0000)

jmol_repr(render_params)¶

Default behavior is to render the triangulation. The actual polygon data is stored in a separate file.

EXAMPLES:

sage: from sage.plot.plot3d.shapes import Torus
sage: G = Torus(1, .5)
sage: G.jmol_repr(G.testing_render_params())
['pmesh obj_1 "obj_1.pmesh"\ncolor pmesh  [102,102,255]']

obj_repr(render_params)¶

Default behavior is to render the triangulation.

EXAMPLES:

sage: from sage.plot.plot3d.shapes import Torus
sage: G = Torus(1, .5)
sage: G.obj_repr(G.default_render_params())
['g obj_1',
 'usemtl ...',
 ['v 0 1 0.5',
 ...
  'f ...'],
 []]

set_texture(texture, **kwds=None)¶

EXAMPLES:

sage: G = dodecahedron(color='red'); G
sage: G.set_texture(color='yellow'); G

tachyon_repr(render_params)¶

Default behavior is to render the triangulation.

EXAMPLES:

sage: from sage.plot.plot3d.shapes import Torus
sage: G = Torus(1, .5)
sage: G.tachyon_repr(G.default_render_params())
['TRI V0 0 1 0.5
...
'texture...']

texture_set()¶

EXAMPLES:

sage: G = dodecahedron(color='red')
sage: G.texture_set()
set([Texture(texture..., red, ff0000)])

x3d_str()¶

EXAMPLES:

sage: sphere().flatten().x3d_str()
"<Transform>\n<Shape><Sphere radius='1.0'/><Appearance><Material diffuseColor='0.4 0.4 1.0' shininess='1' specularColor='0.0 0.0 0.0'/></Appearance></Shape>\n\n</Transform>"

class sage.plot.plot3d.base.RenderParams¶

Bases: sage.structure.sage_object.SageObject

This class is a container for all parameters that may be needed to render triangulate/render an object to a certain format. It can contain both cumulative and global parameters.

Of particular note is the transformation object, which holds the cumulative transformation from the root of the scene graph to this node in the tree.

pop_transform()¶

Remove the last transformation off the stack, resetting self.transform to the previous value.

EXAMPLES:

sage: from sage.plot.plot3d.transform import Transformation
sage: params = sage.plot.plot3d.base.RenderParams()
sage: T = Transformation(trans=(100, 500, 0))
sage: params.push_transform(T)
sage: params.transform.get_matrix()
[  1.0   0.0   0.0 100.0]
[  0.0   1.0   0.0 500.0]
[  0.0   0.0   1.0   0.0]
[  0.0   0.0   0.0   1.0]
sage: params.push_transform(Transformation(trans=(-100, 500, 200)))
sage: params.transform.get_matrix()
[   1.0    0.0    0.0    0.0]
[   0.0    1.0    0.0 1000.0]
[   0.0    0.0    1.0  200.0]
[   0.0    0.0    0.0    1.0]
sage: params.pop_transform()
sage: params.transform.get_matrix()
[  1.0   0.0   0.0 100.0]
[  0.0   1.0   0.0 500.0]
[  0.0   0.0   1.0   0.0]
[  0.0   0.0   0.0   1.0]

push_transform(T)¶

Push a transformation onto the stack, updating self.transform.

EXAMPLES:

sage: from sage.plot.plot3d.transform import Transformation
sage: params = sage.plot.plot3d.base.RenderParams()
sage: params.transform is None
True
sage: T = Transformation(scale=(10,20,30))
sage: params.push_transform(T)
sage: params.transform.get_matrix()
[10.0  0.0  0.0  0.0]
[ 0.0 20.0  0.0  0.0]
[ 0.0  0.0 30.0  0.0]
[ 0.0  0.0  0.0  1.0]
sage: params.push_transform(T)  # scale again
sage: params.transform.get_matrix()
[100.0   0.0   0.0   0.0]
[  0.0 400.0   0.0   0.0]
[  0.0   0.0 900.0   0.0]
[  0.0   0.0   0.0   1.0]

unique_name(desc='name')¶

Returns a unique identifier starting with desc.

EXAMPLES:

sage: params = sage.plot.plot3d.base.RenderParams()
sage: params.unique_name()
'name_1'
sage: params.unique_name()
'name_2'
sage: params.unique_name('texture')
'texture_3'

class sage.plot.plot3d.base.TransformGroup¶

Bases: sage.plot.plot3d.base.Graphics3dGroup

This class is a container for a group of objects with a common transformation.

bounding_box()¶

Returns the bounding box of self, i.e. the box containing the contents of self after applying the transformation.

EXAMPLES:

sage: G = cube()
sage: G.bounding_box()
((-0.5, -0.5, -0.5), (0.5, 0.5, 0.5))
sage: G.scale(4).bounding_box()
((-2.0, -2.0, -2.0), (2.0, 2.0, 2.0))
sage: G.rotateZ(pi/4).bounding_box()
((-0.70710678118654746, -0.70710678118654746, -0.5),
 (0.70710678118654746, 0.70710678118654746, 0.5))

flatten()¶

Try to reduce the depth of the scene tree by consolidating groups and transformations.

EXAMPLES:

sage: G = sphere((1,2,3)).scale(100)
sage: T = G.get_transformation()
sage: T.get_matrix()
[100.0   0.0   0.0   0.0]
[  0.0 100.0   0.0   0.0]
[  0.0   0.0 100.0   0.0]
[  0.0   0.0   0.0   1.0]

sage: G.flatten().get_transformation().get_matrix()
[100.0   0.0   0.0 100.0]
[  0.0 100.0   0.0 200.0]
[  0.0   0.0 100.0 300.0]
[  0.0   0.0   0.0   1.0]

get_transformation()¶

Returns the actual transformation object associated with self.

EXAMPLES:

sage: G = sphere().scale(100)
sage: T = G.get_transformation()
sage: T.get_matrix()
[100.0   0.0   0.0   0.0]
[  0.0 100.0   0.0   0.0]
[  0.0   0.0 100.0   0.0]
[  0.0   0.0   0.0   1.0]

jmol_repr(render_params)¶

Transformations for jmol are applied at the leaf nodes.

EXAMPLES:

sage: G = sphere((1,2,3)).scale(2)
sage: G.jmol_repr(G.default_render_params())
[[['isosurface sphere_1  center {2.0 4.0 6.0} sphere 2.0\ncolor isosurface  [102,102,255]']]]

json_repr(render_params)¶

Transformations are applied at the leaf nodes.

EXAMPLES:

sage: G = cube().rotateX(0.2)
sage: G.json_repr(G.default_render_params())
[["{vertices:[{x:0.5,y:0.589368,z:0.390699},..."]]

obj_repr(render_params)¶

Transformations for .obj files are applied at the leaf nodes.

EXAMPLES:

sage: G = cube().scale(4).translate(1, 2, 3)
sage: G.obj_repr(G.default_render_params())
[[['g obj_1',
   'usemtl ...',
   ['v 3 4 5',
    'v -1 4 5',
    'v -1 0 5',
    'v 3 0 5',
    'v 3 4 1',
    'v -1 4 1',
    'v 3 0 1',
    'v -1 0 1'],
   ['f 1 2 3 4',
    'f 1 5 6 2',
    'f 1 4 7 5',
    'f 6 5 7 8',
    'f 7 4 3 8',
    'f 3 2 6 8'],
   []]]]

tachyon_repr(render_params)¶

Transformations for Tachyon are applied at the leaf nodes.

EXAMPLES:

sage: G = sphere((1,2,3)).scale(2)
sage: G.tachyon_repr(G.default_render_params())
[['Sphere center 2.0 4.0 6.0 Rad 2.0 texture...']]

transform(**kwds)¶

Transforming this entire group can be done by composing transformations.

EXAMPLES:

sage: G = dodecahedron(color='red', opacity=.5) + icosahedron(color='blue')
sage: G
sage: G.transform(scale=(2,1/2,1))
sage: G.transform(trans=(1,1,3))

x3d_str()¶

To apply a transformation to a set of objects in x3d, simply make them all children of an x3d Transform node.

EXAMPLES:

sage: sphere((1,2,3)).x3d_str()
"<Transform translation='1 2 3'>\n<Shape><Sphere radius='1.0'/><Appearance><Material diffuseColor='0.4 0.4 1.0' shininess='1' specularColor='0.0 0.0 0.0'/></Appearance></Shape>\n\n</Transform>"

class sage.plot.plot3d.base.Viewpoint¶

Bases: sage.plot.plot3d.base.Graphics3d

This class represents a viewpoint, necessary for x3d.

In the future, there could be multiple viewpoints, and they could have more properties. (Currently they only hold a position).

x3d_str()¶

EXAMPLES:

sage: sphere((0,0,0), 100).viewpoint().x3d_str()
"<Viewpoint position='0 0 6'/>"

sage.plot.plot3d.base.flatten_list(L)¶

This is an optimized routine to turn a list of lists (of lists ...) into a single list. We generate data in a non-flat format to avoid multiple data copying, and then concatenate it all at the end.

This is NOT recursive, otherwise there would be a lot of redundant copying (which we are trying to avoid in the first place, though at least it would be just the pointers).

EXAMPLES:

sage: from sage.plot.plot3d.base import flatten_list
sage: flatten_list([])
[]
sage: flatten_list([[[[]]]])
[]
sage: flatten_list([['a', 'b'], 'c'])
['a', 'b', 'c']
sage: flatten_list([['a'], [[['b'], 'c'], ['d'], [[['e', 'f', 'g']]]]])
['a', 'b', 'c', 'd', 'e', 'f', 'g']

sage.plot.plot3d.base.max3(v)¶

Return the componentwise maximum of a list of 3-tuples.

EXAMPLES:

sage: from sage.plot.plot3d.base import min3, max3
sage: max3([(-1,2,5), (-3, 4, 2)])
(-1, 4, 5)

sage.plot.plot3d.base.min3(v)¶

Return the componentwise minimum of a list of 3-tuples.

EXAMPLES:

sage: from sage.plot.plot3d.base import min3, max3
sage: min3([(-1,2,5), (-3, 4, 2)])
(-3, 2, 2)

sage.plot.plot3d.base.optimal_aspect_ratios(ratios)¶

sage.plot.plot3d.base.optimal_extra_kwds(v)¶: Given a list v of dictionaries, this function merges them such that later dictionaries have precedence.

sage.plot.plot3d.base.point_list_bounding_box(v)¶

EXAMPLES:

sage: from sage.plot.plot3d.base import point_list_bounding_box
sage: point_list_bounding_box([(1,2,3),(4,5,6),(-10,0,10)])
((-10.0, 0.0, 3.0), (4.0, 5.0, 10.0))
sage: point_list_bounding_box([(float('nan'), float('inf'), float('-inf')), (10,0,10)])
((10.0, 0.0, 10.0), (10.0, 0.0, 10.0))

Base classes for 3D Graphics objects and plotting.¶

Previous topic

Next topic

This Page

Navigation

Base classes for 3D Graphics objects and plotting.¶

Previous topic

Next topic

This Page

Quick search

Navigation