Plotting Functions.

EXAMPLES:

sage: def f(x,y):
...       return math.sin(y*y+x*x)/math.sqrt(x*x+y*y+.0001)
...
sage: P = plot3d(f,(-3,3),(-3,3), adaptive=True, color=rainbow(60, 'rgbtuple'), max_bend=.1, max_depth=15)
sage: P.show()

sage: def f(x,y):
...       return math.exp(x/5)*math.sin(y)
...
sage: P = plot3d(f,(-5,5),(-5,5), adaptive=True, color=['red','yellow'])
sage: from sage.plot.plot3d.plot3d import axes
sage: S = P + axes(6, color='black')
sage: S.show()

We plot “cape man”:

sage: S = sphere(size=.5, color='yellow')

sage: from sage.plot.plot3d.shapes import Cone
sage: S += Cone(.5, .5, color='red').translate(0,0,.3)

sage: S += sphere((.45,-.1,.15), size=.1, color='white') + sphere((.51,-.1,.17), size=.05, color='black')
sage: S += sphere((.45, .1,.15),size=.1, color='white') + sphere((.51, .1,.17), size=.05, color='black')
sage: S += sphere((.5,0,-.2),size=.1, color='yellow')
sage: def f(x,y): return math.exp(x/5)*math.cos(y)
sage: P = plot3d(f,(-5,5),(-5,5), adaptive=True, color=['red','yellow'], max_depth=10)
sage: cape_man = P.scale(.2) + S.translate(1,0,0)
sage: cape_man.show(aspect_ratio=[1,1,1])

AUTHORS:

• Tom Boothby: adaptive refinement triangles
• Josh Kantor: adaptive refinement triangles
• Robert Bradshaw (2007-08): initial version of this file
• William Stein (2007-12, 2008-01): improving 3d plotting
• Oscar Lazo, William Cauchois, Jason Grout (2009-2010): Adding coordinate transformations

class sage.plot.plot3d.plot3d.Cylindrical(dep_var, indep_vars)

Bases: sage.plot.plot3d.plot3d._Coordinates

A cylindrical coordinate system for use with plot3d(transformation=...) where the position of a point is specified by three numbers:

• the radial distance (radius) from the -axis
• the azimuth angle (azimuth) from the positive -axis
• the height or altitude (height) above the -plane

These three variables must be specified in the constructor.

EXAMPLES:

Construct a cylindrical transformation for a function for height in terms of radius and azimuth:

sage: T = Cylindrical('height', ['radius', 'azimuth'])

If we construct some concrete variables, we can get a transformation:

sage: r, theta, z = var('r theta z')
sage: T.transform(radius=r, azimuth=theta, height=z)
(r*cos(theta), r*sin(theta), z)

We can plot with this transform. Remember that the independent variable is the height, and the dependent variables are the radius and the azimuth (in that order):

sage: plot3d(9-r^2, (r, 0, 3), (theta, 0, pi), transformation=T)

We next graph the function where the radius is constant:

sage: S=Cylindrical('radius', ['azimuth', 'height'])
sage: theta,z=var('theta, z')
sage: plot3d(3, (theta,0,2*pi), (z, -2, 2), transformation=S)

See also cylindrical_plot3d() for more examples of plotting in cylindrical coordinates.

transform(radius=None, azimuth=None, height=None)

A cylindrical coordinates transform.

EXAMPLE:

sage: T = Cylindrical('height', ['azimuth', 'radius'])
sage: T.transform(radius=var('r'), azimuth=var('theta'), height=var('z'))
(r*cos(theta), r*sin(theta), z)

class sage.plot.plot3d.plot3d.Spherical(dep_var, indep_vars)

Bases: sage.plot.plot3d.plot3d._Coordinates

A spherical coordinate system for use with plot3d(transformation=...) where the position of a point is specified by three numbers:

• the radial distance (radius) from the origin
• the azimuth angle (azimuth) from the positive -axis
• the inclination angle (inclination) from the positive -axis

These three variables must be specified in the constructor.

EXAMPLES:

Construct a spherical transformation for a function for the radius in terms of the azimuth and inclination:

sage: T = Spherical('radius', ['azimuth', 'inclination'])

If we construct some concrete variables, we can get a transformation in terms of those variables:

sage: r, phi, theta = var('r phi theta')
sage: T.transform(radius=r, azimuth=theta, inclination=phi)
(r*sin(phi)*cos(theta), r*sin(phi)*sin(theta), r*cos(phi))

We can plot with this transform. Remember that the independent variable is the radius, and the dependent variables are the azimuth and the inclination (in that order):

sage: plot3d(phi * theta, (theta, 0, pi), (phi, 0, 1), transformation=T)

We next graph the function where the inclination angle is constant:

sage: S=Spherical('inclination', ['radius', 'azimuth'])
sage: r,theta=var('r,theta')
sage: plot3d(3, (r,0,3), (theta, 0, 2*pi), transformation=S)

See also spherical_plot3d() for more examples of plotting in spherical coordinates.

transform(radius=None, azimuth=None, inclination=None)

A spherical coordinates transform.

EXAMPLE:

sage: T = Spherical('radius', ['azimuth', 'inclination'])
sage: T.transform(radius=var('r'), azimuth=var('theta'), inclination=var('phi'))
(r*sin(phi)*cos(theta), r*sin(phi)*sin(theta), r*cos(phi))

class sage.plot.plot3d.plot3d.TrivialTriangleFactory

smooth_triangle(a, b, c, da, db, dc, color=None)

triangle(a, b, c, color=None)

sage.plot.plot3d.plot3d.axes(scale=1, radius=None, **kwds)

sage.plot.plot3d.plot3d.cylindrical_plot3d(f, urange, vrange, **kwds)

Plots a function in cylindrical coordinates. This function is equivalent to:

sage: r,u,v=var('r,u,v')
sage: f=u*v; urange=(u,0,pi); vrange=(v,0,pi)
sage: T = (r*cos(u), r*sin(u), v, [u,v])
sage: plot3d(f, urange, vrange, transformation=T)

or equivalently:

sage: T = Cylindrical('radius', ['azimuth', 'height'])
sage: f=lambda u,v: u*v; urange=(u,0,pi); vrange=(v,0,pi)
sage: plot3d(f, urange, vrange, transformation=T)

INPUT:

• f - a symbolic expression or function of two variables, representing the radius from the -axis.
• urange - a 3-tuple (u, u_min, u_max), the domain of the azimuth variable.
• vrange - a 3-tuple (v, v_min, v_max), the domain of the elevation () variable.

EXAMPLES:

A portion of a cylinder of radius 2:

sage: theta,z=var('theta,z')
sage: cylindrical_plot3d(2,(theta,0,3*pi/2),(z,-2,2))

Some random figures:

sage: cylindrical_plot3d(cosh(z),(theta,0,2*pi),(z,-2,2))

sage: cylindrical_plot3d(e^(-z^2)*(cos(4*theta)+2)+1,(theta,0,2*pi),(z,-2,2),plot_points=[80,80]).show(aspect_ratio=(1,1,1))

sage.plot.plot3d.plot3d.plot3d(f, urange, vrange, adaptive=False, transformation=None, **kwds)

INPUT:

• f - a symbolic expression or function of 2 variables
• urange - a 2-tuple (u_min, u_max) or a 3-tuple (u, u_min, u_max)
• vrange - a 2-tuple (v_min, v_max) or a 3-tuple (v, v_min, v_max)
• adaptive - (default: False) whether to use adaptive refinement to draw the plot (slower, but may look better). This option does NOT work in conjuction with a transformation (see below).
• mesh - bool (default: False) whether to display mesh grid lines
• dots - bool (default: False) whether to display dots at mesh grid points
• plot_points - (default: “automatic”) initial number of sample points in each direction; an integer or a pair of integers
• transformation - (default: None) a transformation to apply. May be a 3 or 4-tuple (x_func, y_func, z_func, independent_vars) where the first 3 items indicate a transformation to cartesian coordinates (from your coordinate system) in terms of u, v, and the function variable fvar (for which the value of f will be substituted). If a 3-tuple is specified, the independent variables are chosen from the range variables. If a 4-tuple is specified, the 4th element is a list of independent variables. transformation may also be a predefined coordinate system transformation like Spherical or Cylindrical.

Note

mesh and dots are not supported when using the Tachyon raytracer renderer.

EXAMPLES: We plot a 3d function defined as a Python function:

sage: plot3d(lambda x, y: x^2 + y^2, (-2,2), (-2,2))

We plot the same 3d function but using adaptive refinement:

sage: plot3d(lambda x, y: x^2 + y^2, (-2,2), (-2,2), adaptive=True)

Adaptive refinement but with more points:

sage: plot3d(lambda x, y: x^2 + y^2, (-2,2), (-2,2), adaptive=True, initial_depth=5)

We plot some 3d symbolic functions:

sage: var('x,y')
(x, y)
sage: plot3d(x^2 + y^2, (x,-2,2), (y,-2,2))
sage: plot3d(sin(x*y), (x, -pi, pi), (y, -pi, pi))

We give a plot with extra sample points:

sage: var('x,y')
(x, y)
sage: plot3d(sin(x^2+y^2),(x,-5,5),(y,-5,5), plot_points=200)
sage: plot3d(sin(x^2+y^2),(x,-5,5),(y,-5,5), plot_points=[10,100])

A 3d plot with a mesh:

sage: var('x,y')
(x, y)
sage: plot3d(sin(x-y)*y*cos(x),(x,-3,3),(y,-3,3), mesh=True)     

Two wobby translucent planes:

sage: x,y = var('x,y')
sage: P = plot3d(x+y+sin(x*y), (x,-10,10),(y,-10,10), opacity=0.87, color='blue')
sage: Q = plot3d(x-2*y-cos(x*y),(x,-10,10),(y,-10,10),opacity=0.3,color='red')
sage: P + Q

We draw two parametric surfaces and a transparent plane:

sage: L = plot3d(lambda x,y: 0, (-5,5), (-5,5), color="lightblue", opacity=0.8)
sage: P = plot3d(lambda x,y: 4 - x^3 - y^2, (-2,2), (-2,2), color='green')
sage: Q = plot3d(lambda x,y: x^3 + y^2 - 4, (-2,2), (-2,2), color='orange')
sage: L + P + Q

We draw the “Sinus” function (water ripple-like surface):

sage: x, y = var('x y')
sage: plot3d(sin(pi*(x^2+y^2))/2,(x,-1,1),(y,-1,1))

Hill and valley (flat surface with a bump and a dent):

sage: x, y = var('x y')
sage: plot3d( 4*x*exp(-x^2-y^2), (x,-2,2), (y,-2,2))

An example of a transformation:

sage: r, phi, z = var('r phi z')
sage: trans=(r*cos(phi),r*sin(phi),z)
sage: plot3d(cos(r),(r,0,17*pi/2),(phi,0,2*pi),transformation=trans,opacity=0.87).show(aspect_ratio=(1,1,2),frame=False)

Many more examples of transformations:

sage: u, v, w = var('u v w')
sage: rectangular=(u,v,w)
sage: spherical=(w*cos(u)*sin(v),w*sin(u)*sin(v),w*cos(v))
sage: cylindric_radial=(w*cos(u),w*sin(u),v)
sage: cylindric_axial=(v*cos(u),v*sin(u),w)
sage: parabolic_cylindrical=(w*v,(v^2-w^2)/2,u)

Plot a constant function of each of these to get an idea of what it does:

sage: A = plot3d(2,(u,-pi,pi),(v,0,pi),transformation=rectangular,plot_points=[100,100])
sage: B = plot3d(2,(u,-pi,pi),(v,0,pi),transformation=spherical,plot_points=[100,100])
sage: C = plot3d(2,(u,-pi,pi),(v,0,pi),transformation=cylindric_radial,plot_points=[100,100])
sage: D = plot3d(2,(u,-pi,pi),(v,0,pi),transformation=cylindric_axial,plot_points=[100,100])
sage: E = plot3d(2,(u,-pi,pi),(v,-pi,pi),transformation=parabolic_cylindrical,plot_points=[100,100])
sage: @interact
... def _(which_plot=[A,B,C,D,E]):
...       show(which_plot)
<html>...

Now plot a function:

sage: g=3+sin(4*u)/2+cos(4*v)/2
sage: F = plot3d(g,(u,-pi,pi),(v,0,pi),transformation=rectangular,plot_points=[100,100])
sage: G = plot3d(g,(u,-pi,pi),(v,0,pi),transformation=spherical,plot_points=[100,100])
sage: H = plot3d(g,(u,-pi,pi),(v,0,pi),transformation=cylindric_radial,plot_points=[100,100])
sage: I = plot3d(g,(u,-pi,pi),(v,0,pi),transformation=cylindric_axial,plot_points=[100,100])
sage: J = plot3d(g,(u,-pi,pi),(v,0,pi),transformation=parabolic_cylindrical,plot_points=[100,100])
sage: @interact
... def _(which_plot=[F, G, H, I, J]):
...       show(which_plot)
<html>...

TESTS:

Make sure the transformation plots work:

sage: show(A + B + C + D + E)
sage: show(F + G + H + I + J)

Listing the same plot variable twice gives an error:

sage: x, y = var('x y')
sage: plot3d( 4*x*exp(-x^2-y^2), (x,-2,2), (x,-2,2))
...
ValueError: range variables should be distinct, but there are duplicates

sage.plot.plot3d.plot3d.plot3d_adaptive(f, x_range, y_range, color='automatic', grad_f=None, max_bend=0.5, max_depth=5, initial_depth=4, num_colors=128, **kwds)

Adaptive 3d plotting of a function of two variables.

This is used internally by the plot3d command when the option adaptive=True is given.

INPUT:

• f - a symbolic function or a Python function of 3 variables.
• x_range - x range of values: 2-tuple (xmin, xmax) or 3-tuple (x,xmin,xmax)
• y_range - y range of values: 2-tuple (ymin, ymax) or 3-tuple (y,ymin,ymax)
• grad_f - gradient of f as a Python function
• color - “automatic” - a rainbow of num_colors colors
• num_colors - (default: 128) number of colors to use with default color
• max_bend - (default: 0.5)
• max_depth - (default: 5)
• initial_depth - (default: 4)
• **kwds - standard graphics parameters

EXAMPLES: We plot :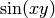

sage: from sage.plot.plot3d.plot3d import plot3d_adaptive
sage: x,y=var('x,y'); plot3d_adaptive(sin(x*y), (x,-pi,pi), (y,-pi,pi), initial_depth=5)

sage.plot.plot3d.plot3d.spherical_plot3d(f, urange, vrange, **kwds)

Plots a function in spherical coordinates. This function is equivalent to:

sage: r,u,v=var('r,u,v')
sage: f=u*v; urange=(u,0,pi); vrange=(v,0,pi)
sage: T = (r*cos(u)*sin(v), r*sin(u)*sin(v), r*cos(v), [u,v])
sage: plot3d(f, urange, vrange, transformation=T)

or equivalently:

sage: T = Spherical('radius', ['azimuth', 'inclination'])
sage: f=lambda u,v: u*v; urange=(u,0,pi); vrange=(v,0,pi)
sage: plot3d(f, urange, vrange, transformation=T)

INPUT:

• f - a symbolic expression or function of two variables.
• urange - a 3-tuple (u, u_min, u_max), the domain of the azimuth variable.
• vrange - a 3-tuple (v, v_min, v_max), the domain of the inclination variable.

EXAMPLES:

A sphere of radius 2:

sage: x,y=var('x,y')
sage: spherical_plot3d(2,(x,0,2*pi),(y,0,pi))

A drop of water:

sage: x,y=var('x,y')
sage: spherical_plot3d(e^-y,(x,0,2*pi),(y,0,pi),opacity=0.5).show(frame=False)

An object similar to a heart:

sage: x,y=var('x,y')
sage: spherical_plot3d((2+cos(2*x))*(y+1),(x,0,2*pi),(y,0,pi),rgbcolor=(1,.1,.1))

Some random figures:

sage: x,y=var('x,y')
sage: spherical_plot3d(1+sin(5*x)/5,(x,0,2*pi),(y,0,pi),rgbcolor=(1,0.5,0),plot_points=(80,80),opacity=0.7)

sage: x,y=var('x,y')
sage: spherical_plot3d(1+2*cos(2*y),(x,0,3*pi/2),(y,0,pi)).show(aspect_ratio=(1,1,1))