The Tachyon 3D Ray Tracer

Given any 3D graphics object one can compute a raytraced representation by typing show(viewer='tachyon'). For example, we draw two translucent spheres that contain a red tube, and render the result using Tachyon.

sage: S = sphere(opacity=0.8, aspect_ratio=[1,1,1])
sage: L = line3d([(0,0,0),(2,0,0)], thickness=10, color='red')
sage: M = S + S.translate((2,0,0)) + L
sage: M.show(viewer='tachyon')

One can also directly control Tachyon, which gives a huge amount of flexibility. For example, here we directly use Tachyon to draw 3 spheres on the coordinate axes. Notice that the result is gorgeous:

sage: t = Tachyon(xres=500,yres=500, camera_center=(2,0,0))
sage: t.light((4,3,2), 0.2, (1,1,1))
sage: t.texture('t2', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(1,0,0))
sage: t.texture('t3', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(0,1,0))
sage: t.texture('t4', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(0,0,1))
sage: t.sphere((0,0.5,0), 0.2, 't2')
sage: t.sphere((0.5,0,0), 0.2, 't3')
sage: t.sphere((0,0,0.5), 0.2, 't4')
sage: t.show()

AUTHOR:

• John E. Stone (johns@megapixel.com): wrote tachyon ray tracer
• William Stein: sage-tachyon interface
• Joshua Kantor: 3d function plotting
• Tom Boothby: 3d function plotting n’stuff
• Leif Hille: key idea for bugfix for texfunc issue (trac #799)
• Marshall Hampton: improved doctests, rings, axis-aligned boxes.

TODO:

• clean up trianglefactory stuff

class sage.plot.plot3d.tachyon.Axis_aligned_box(min_p, max_p, texture)

Box with axis-aligned edges with the given min and max coordinates.

str()

Returns the scene string of the axis-aligned box.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import Axis_aligned_box
sage: aab = Axis_aligned_box((0,0,0),(1,1,1),'s')
sage: aab.str()
'\n        box min  0.0 0.0 0.0  max  1.0 1.0 1.0  s\n        '

class sage.plot.plot3d.tachyon.Cylinder(center, axis, radius, texture)

An infinite cylinder.

str()

Returns the scene string of the cylinder.

EXAMPLES:

sage: t = Tachyon()
sage: from sage.plot.plot3d.tachyon import Cylinder
sage: c = Cylinder((0,0,0),(1,1,1),.1,'s')
sage: c.str()
'\n        cylinder center  0.0 0.0 0.0  axis  1.0 1.0 1.0  rad 0.1 s\n        '

class sage.plot.plot3d.tachyon.FCylinder(base, apex, radius, texture)

A finite cylinder.

str()

Returns the scene string of the finite cylinder.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import FCylinder
sage: fc = FCylinder((0,0,0),(1,1,1),.1,'s')
sage: fc.str()
'\n        fcylinder base  0.0 0.0 0.0  apex  1.0 1.0 1.0  rad 0.1 s\n        '

class sage.plot.plot3d.tachyon.FractalLandscape(res, scale, center, texture)

Axis-aligned fractal landscape. Does not seem very useful at the moment, but perhaps will be improved in the future.

str()

Returns the scene string of the fractal landscape.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import FractalLandscape
sage: fl = FractalLandscape([20,20],[30,30],[1,2,3],'s')
sage: fl.str()
'\n        scape res  20 20  scale  30 30  center  1.0 2.0 3.0  s\n        '

class sage.plot.plot3d.tachyon.Light(center, radius, color)

Represents lighting objects.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import Light
sage: q = Light((1,1,1),1,(1,1,1))
sage: q._center
(1, 1, 1)

str()

Returns the tachyon string defining the light source.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import Light
sage: q = Light((1,1,1),1,(1,1,1))
sage: q._radius
1

class sage.plot.plot3d.tachyon.ParametricPlot(f, t_0, t_f, tex, r=0.10000000000000001, cylinders=True, min_depth=4, max_depth=8, e_rel=0.01, e_abs=0.01)

Parametric plotting routines.

str()

Returns the tachyon string representation of the parameterized curve.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import ParametricPlot
sage: t = var('t')
sage: f = lambda t: (t,t^2,t^3)
sage: q = ParametricPlot(f,0,1,'s')
sage: q.str()[9:69]
'sphere center  0.0 0.0 0.0  rad 0.1 s\n        \n        fcyli'

tol(est, val)

Check relative, then absolute tolerance. If both fail, return False. This is a zero-safe error checker.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import ParametricPlot
sage: t = var('t')
sage: f = lambda t: (t,t^2,t^3)
sage: q = ParametricPlot(f,0,1,'s')
sage: q.tol([0,0,0],[1,0,0])
False
sage: q.tol([0,0,0],[.0001,0,0])
True

class sage.plot.plot3d.tachyon.Plane(center, normal, texture)

An infinite plane.

str()

Returns the scene string of the plane.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import Plane
sage: p = Plane((1,2,3),(1,2,4),'s')
sage: p.str()
'\n        plane center  1.0 2.0 3.0  normal  1.0 2.0 4.0  s\n        '

class sage.plot.plot3d.tachyon.Ring(center, normal, inner, outer, texture)

An annulus of zero thickness.

str()

Returns the scene string of the ring.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import Ring
sage: r = Ring((0,0,0), (1,1,0), 1.0, 2.0, 's')
sage: r.str()
'\n        ring center  0.0 0.0 0.0  normal  1.0 1.0 0.0  inner 1.0 outer 2.0 s\n        '

class sage.plot.plot3d.tachyon.Sphere(center, radius, texture)

A class for creating spheres in tachyon.

str()

Returns the scene string for the sphere.

EXAMPLES:

sage: t = Tachyon()
sage: from sage.plot.plot3d.tachyon import Sphere
sage: t.texture('r', color=(.8,0,0), ambient = .1)
sage: s = Sphere((1,1,1),1,'r')
sage: s.str()
'\n        sphere center  1.0 1.0 1.0  rad 1.0 r\n        '

class sage.plot.plot3d.tachyon.Tachyon(xres=350, yres=350, zoom=1.0, antialiasing=False, aspectratio=1.0, raydepth=8, camera_center=(-3, 0, 0), updir=(0, 0, 1), look_at=(0, 0, 0), viewdir=None, projection='PERSPECTIVE')

Bases: sage.structure.sage_object.SageObject

Create a scene the can be rendered using the Tachyon ray tracer.

INPUT:

• xres - (default 350)
• yres - (default 350)
• zoom - (default 1.0)
• antialiasing - (default False)
• aspectratio - (default 1.0)
• raydepth - (default 5)
• camera_center - (default (-3, 0, 0))
• updir - (default (0, 0, 1))
• look_at - (default (0,0,0))
• viewdir - (default None)
• projection - (default ‘PERSPECTIVE’)

OUTPUT: A Tachyon 3d scene.

Note that the coordinates are by default such that is up, positive is to the {left} and is toward you. This is not oriented according to the right hand rule.

EXAMPLES: Spheres along the twisted cubic.

sage: t = Tachyon(xres=512,yres=512, camera_center=(3,0.3,0))
sage: t.light((4,3,2), 0.2, (1,1,1))
sage: t.texture('t0', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(1.0,0,0))
sage: t.texture('t1', ambient=0.1, diffuse=0.9, specular=0.3, opacity=1.0, color=(0,1.0,0))
sage: t.texture('t2', ambient=0.2,diffuse=0.7, specular=0.5, opacity=0.7, color=(0,0,1.0))
sage: k=0
sage: for i in srange(-1,1,0.05):
...    k += 1
...    t.sphere((i,i^2-0.5,i^3), 0.1, 't%s'%(k%3))
...
sage: t.show()

Another twisted cubic, but with a white background, got by putting infinite planes around the scene.

sage: t = Tachyon(xres=512,yres=512, camera_center=(3,0.3,0), raydepth=8)
sage: t.light((4,3,2), 0.2, (1,1,1))
sage: t.texture('t0', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(1.0,0,0))
sage: t.texture('t1', ambient=0.1, diffuse=0.9, specular=0.3, opacity=1.0, color=(0,1.0,0))
sage: t.texture('t2', ambient=0.2,diffuse=0.7, specular=0.5, opacity=0.7, color=(0,0,1.0))
sage: t.texture('white', color=(1,1,1))
sage: t.plane((0,0,-1), (0,0,1), 'white')
sage: t.plane((0,-20,0), (0,1,0), 'white')
sage: t.plane((-20,0,0), (1,0,0), 'white')

sage: k=0
sage: for i in srange(-1,1,0.05):
...    k += 1
...    t.sphere((i,i^2 - 0.5,i^3), 0.1, 't%s'%(k%3))
...    t.cylinder((0,0,0), (0,0,1), 0.05,'t1')
...
sage: t.show()

Many random spheres:

sage: t = Tachyon(xres=512,yres=512, camera_center=(2,0.5,0.5), look_at=(0.5,0.5,0.5), raydepth=4)
sage: t.light((4,3,2), 0.2, (1,1,1))
sage: t.texture('t0', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(1.0,0,0))
sage: t.texture('t1', ambient=0.1, diffuse=0.9, specular=0.3, opacity=1.0, color=(0,1.0,0))
sage: t.texture('t2', ambient=0.2, diffuse=0.7, specular=0.5, opacity=0.7, color=(0,0,1.0))
sage: k=0
sage: for i in range(100):
...    k += 1
...    t.sphere((random(),random(), random()), random()/10, 't%s'%(k%3))
...
sage: t.show()

Points on an elliptic curve, their height indicated by their height above the axis:

sage: t = Tachyon(camera_center=(5,2,2), look_at=(0,1,0))
sage: t.light((10,3,2), 0.2, (1,1,1))
sage: t.texture('t0', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(1,0,0))
sage: t.texture('t1', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(0,1,0))
sage: t.texture('t2', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(0,0,1))
sage: E = EllipticCurve('37a')
sage: P = E([0,0])
sage: Q = P
sage: n = 100
sage: for i in range(n):   # increase 20 for a better plot
...    Q = Q + P
...    t.sphere((Q[1], Q[0], ZZ(i)/n), 0.1, 't%s'%(i%3))
...
sage: t.show()

A beautiful picture of rational points on a rank 1 elliptic curve.

sage: t = Tachyon(xres=1000, yres=800, camera_center=(2,7,4), look_at=(2,0,0), raydepth=4)
sage: t.light((10,3,2), 1, (1,1,1))
sage: t.light((10,-3,2), 1, (1,1,1))
sage: t.texture('black', color=(0,0,0))
sage: t.texture('red', color=(1,0,0))
sage: t.texture('grey', color=(.9,.9,.9))
sage: t.plane((0,0,0),(0,0,1),'grey')
sage: t.cylinder((0,0,0),(1,0,0),.01,'black')
sage: t.cylinder((0,0,0),(0,1,0),.01,'black')
sage: E = EllipticCurve('37a')
sage: P = E([0,0])
sage: Q = P
sage: n = 100
sage: for i in range(n):
...    Q = Q + P
...    c = i/n + .1
...    t.texture('r%s'%i,color=(float(i/n),0,0))
...    t.sphere((Q[0], -Q[1], .01), .04, 'r%s'%i)
...
...
sage: t.show()    # long time, e.g., 10-20 seconds

A beautiful spiral.

sage: t = Tachyon(xres=800,yres=800, camera_center=(2,5,2), look_at=(2.5,0,0))
sage: t.light((0,0,100), 1, (1,1,1))
sage: t.texture('r', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(1,0,0))
sage: for i in srange(0,50,0.1):
...    t.sphere((i/10,sin(i),cos(i)), 0.05, 'r')
...
sage: t.texture('white', color=(1,1,1), opacity=1, specular=1, diffuse=1)
sage: t.plane((0,0,-100), (0,0,-100), 'white')
sage: t.show()

axis_aligned_box(min_p, max_p, texture)

Creates an axis-aligned box with minimal point min_p and maximum point max_p.

EXAMPLES:

sage: t = Tachyon()
sage: t.axis_aligned_box((0,0,0),(2,2,2),'s')

cylinder(center, axis, radius, texture)

Creates the scene information for a infinite cylinder with the given center, axis direction, radius, and texture.

EXAMPLES:

sage: t = Tachyon()
sage: t.texture('c')
sage: t.cylinder((0,0,0),(-1,-1,-1),.1,'c')

fcylinder(base, apex, radius, texture)

Finite cylinders are almost the same as infinite ones, but the center and length of the axis determine the extents of the cylinder. The finite cylinder is also really a shell, it doesn’t have any caps. If you need to close off the ends of the cylinder, use two ring objects, with the inner radius set to 0.0 and the normal set to be the axis of the cylinder. Finite cylinders are built this way to enhance speed.

EXAMPLES:

sage: t = Tachyon()
sage: t.fcylinder((1,1,1),(1,2,3),.01,'s')
sage: len(t.str())
423

fractal_landscape(res, scale, center, texture)

Axis-aligned fractal landscape. Not very useful at the moment.

EXAMPLES:

sage: t = Tachyon()
sage: t.texture('s')
sage: t.fractal_landscape([30,30],[80,80],[0,0,0],'s')
sage: len(t._objects)
2

light(center, radius, color)

Creates a light source of the given center, radius, and color.

EXAMPLES:

sage: q = Tachyon()
sage: q.light((1,1,1),1.0,(.2,0,.8))
sage: q.str().split('\n')[17]
'        light center  1.0 1.0 1.0 '

parametric_plot(f, t_0, t_f, tex, r=0.10000000000000001, cylinders=True, min_depth=4, max_depth=8, e_rel=0.01, e_abs=0.01)

Plots a space curve as a series of spheres and finite cylinders. Example (twisted cubic)

sage: f = lambda t: (t,t^2,t^3)
sage: t = Tachyon(camera_center=(5,0,4))
sage: t.texture('t')
sage: t.light((-20,-20,40), 0.2, (1,1,1))
sage: t.parametric_plot(f,-5,5,'t',min_depth=6)

plane(center, normal, texture)

Creates an infinite plane with the given center and normal.

EXAMPLES:

sage: t = Tachyon()
sage: t.plane((0,0,0),(1,1,1),'s')
sage: t.str()[338:380]
'plane center  0.0 0.0 0.0  normal  1.0 1.0'

plot(f, (xmin, xmax), (ymin, ymax), texture, grad_f=None, max_bend=0.69999999999999996, max_depth=5, initial_depth=3, num_colors=None)

INPUT:

• f - Function of two variables, which returns a float (or coercible to a float) (xmin,xmax)
• (ymin,ymax) - defines the rectangle to plot over texture: Name of texture to be used Optional arguments:
• grad_f - gradient function. If specified, smooth triangles will be used.
• max_bend - Cosine of the threshold angle between triangles used to determine whether or not to recurse after the minimum depth
• max_depth - maximum recursion depth. Maximum triangles plotted =
• initial_depth - minimum recursion depth. No error-tolerance checking is performed below this depth. Minimum triangles plotted:
• num_colors - Number of rainbow bands to color the plot with. Texture supplied will be cloned (with different colors) using the texture_recolor method of the Tachyon object.

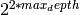
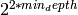
Plots a function by constructing a mesh with nonstandard sampling density without gaps. At very high resolutions (depths 10) it becomes very slow. Cython may help. Complexity is approx. 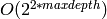. This algorithm has been optimized for speed, not memory - values from f(x,y) are recycled rather than calling the function multiple times. At high recursion depth, this may cause problems for some machines.

Flat Triangles:

sage: t = Tachyon(xres=512,yres=512, camera_center=(4,-4,3),viewdir=(-4,4,-3), raydepth=4)
sage: t.light((4.4,-4.4,4.4), 0.2, (1,1,1))
sage: def f(x,y): return float(sin(x*y))
sage: t.texture('t0', ambient=0.1, diffuse=0.9, specular=0.1,  opacity=1.0, color=(1.0,0,0))
sage: t.plot(f,(-4,4),(-4,4),"t0",max_depth=5,initial_depth=3, num_colors=60)  # increase min_depth for better picture
sage: t.show()

Plotting with Smooth Triangles (requires explicit gradient function):

sage: t = Tachyon(xres=512,yres=512, camera_center=(4,-4,3),viewdir=(-4,4,-3), raydepth=4)
sage: t.light((4.4,-4.4,4.4), 0.2, (1,1,1))
sage: def f(x,y): return float(sin(x*y))
sage: def g(x,y): return ( float(y*cos(x*y)), float(x*cos(x*y)), 1 )
sage: t.texture('t0', ambient=0.1, diffuse=0.9, specular=0.1,  opacity=1.0, color=(1.0,0,0))
sage: t.plot(f,(-4,4),(-4,4),"t0",max_depth=5,initial_depth=3, grad_f = g)  # increase min_depth for better picture
sage: t.show()

Preconditions: f is a scalar function of two variables, grad_f is None or a triple-valued function of two variables, min_x != max_x, min_y != max_y

sage: f = lambda x,y: x*y
sage: t = Tachyon()
sage: t.plot(f,(2.,2.),(-2.,2.),'')
...
ValueError: Plot rectangle is really a line.  Make sure min_x != max_x and min_y != max_y.

ring(center, normal, inner, outer, texture)

Creates the scene information for a ring with the given parameters.

EXAMPLES:

sage: t = Tachyon()
sage: t.ring([0,0,0], [0,0,1], 1.0, 2.0, 's')
sage: t._objects[0]._center
[0, 0, 0]

save(filename='sage.png', verbose=0, block=True, extra_opts='')

INPUT:

• filename - (default: ‘sage.png’) output filename; the extension of the filename determines the type. Supported types include:
• tga - 24-bit (uncompressed)
• bmp - 24-bit Windows BMP (uncompressed)
• ppm - 24-bit PPM (uncompressed)
• rgb - 24-bit SGI RGB (uncompressed)
• png - 24-bit PNG (compressed, lossless)
• verbose - integer; (default: 0)
• 0 - silent
• 1 - some output
• 2 - very verbose output
• block - bool (default: True); if False, run the rendering command in the background.
• extra_opts - passed directly to tachyon command line. Use tachyon_rt.usage() to see some of the possibilities.

EXAMPLES:

sage: q = Tachyon()
sage: q.light((1,1,11), 1,(1,1,1))
sage: q.texture('s')
sage: q.sphere((0,0,0),1,'s')
sage: tempname = tmp_filename()
sage: q.save(tempname)
sage: os.system('rm ' + tempname)
0

show(verbose=0, extra_opts='')

Creates a PNG file of the scene.

EXAMPLES:

sage: q = Tachyon()
sage: q.light((-1,-1,10), 1,(1,1,1))
sage: q.texture('s')
sage: q.sphere((0,0,0),1,'s')
sage: q.show(verbose = False)

smooth_triangle(vertex_1, vertex_2, vertex_3, normal_1, normal_2, normal_3, texture)

Creates a triangle along with a normal vector for smoothing.

EXAMPLES:

sage: t = Tachyon()
sage: t.light((1,1,1),.1,(1,1,1))
sage: t.texture('s')
sage: t.smooth_triangle([0,0,0],[0,0,1],[0,1,0],[0,1,1],[-1,1,2],[3,0,0],'s')
sage: t._objects[2]
[0, 0, 0] [0, 0, 1] [0, 1, 0] s [0, 1, 1] [-1, 1, 2] [3, 0, 0]

sphere(center, radius, texture)

Creates the scene information for a sphere with the given center, radius, and texture.

EXAMPLES:

sage: t = Tachyon()
sage: t.texture('sphere_texture')
sage: t.sphere((1,2,3), .1, 'sphere_texture')
sage: t._objects[1].str()
'\n        sphere center  1.0 2.0 3.0  rad 0.1 sphere_texture\n        '

str()

Returns the complete tachyon scene file as a string.

EXAMPLES:

sage: t = Tachyon(xres=500,yres=500, camera_center=(2,0,0))
sage: t.light((4,3,2), 0.2, (1,1,1))
sage: t.texture('t2', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(1,0,0))
sage: t.texture('t3', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(0,1,0))
sage: t.texture('t4', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(0,0,1))
sage: t.sphere((0,0.5,0), 0.2, 't2')
sage: t.sphere((0.5,0,0), 0.2, 't3')
sage: t.sphere((0,0,0.5), 0.2, 't4')
sage: t.str().find('PLASTIC')
567

texfunc(type=0, center=(0, 0, 0), rotate=(0, 0, 0), scale=(1, 1, 1))

INPUT:

• type - (default: 0)
  0. No special texture, plain shading
  1. 3D checkerboard function, like a rubik’s cube
  2. Grit Texture, randomized surface color
  3. 3D marble texture, uses object’s base color
  4. 3D wood texture, light and dark brown, not very good yet
  5. 3D gradient noise function (can’t remember what it looks like)
  6. Don’t remember
  7. Cylindrical Image Map, requires ppm filename (don’t know how to specify name in sage?!)
  8. Spherical Image Map, requires ppm filename (don’t know how to specify name in sage?!)
  9. Planar Image Map, requires ppm filename (don’t know how to specify name in sage?!)
• center - (default: (0,0,0))
• rotate - (default: (0,0,0))
• scale - (default: (1,1,1))

EXAMPLES: We draw an infinite checkboard:

sage: t = Tachyon(camera_center=(2,7,4), look_at=(2,0,0))
sage: t.texture('black', color=(0,0,0), texfunc=1)
sage: t.plane((0,0,0),(0,0,1),'black')
sage: t.show()

texture(name, ambient=0.20000000000000001, diffuse=0.80000000000000004, specular=0.0, opacity=1.0, color=(1.0, 0.0, 0.5), texfunc=0, phong=0, phongsize=0.5, phongtype='PLASTIC')

INPUT:

• name - string; the name of the texture (to be used later)
• ambient - (default: 0.2)
• diffuse - (default: 0.8)
• specular - (default: 0.0)
• opacity - (default: 1.0)
• color - (default: (1.0,0.0,0.5))
• texfunc - (default: 0); a texture function; this is either the output of self.texfunc, or a number between 0 and 9, inclusive. See the docs for self.texfunc.
• phong - (default: 0)
• phongsize - (default: 0.5)
• phongtype - (default: “PLASTIC”)

EXAMPLES: We draw a scene with 4 sphere that illustrates various uses of the texture command:

sage: t = Tachyon(camera_center=(2,5,4), look_at=(2,0,0), raydepth=6)
sage: t.light((10,3,4), 1, (1,1,1))
sage: t.texture('mirror', ambient=0.05, diffuse=0.05, specular=.9, opacity=0.9, color=(.8,.8,.8))
sage: t.texture('grey', color=(.8,.8,.8), texfunc=3)
sage: t.plane((0,0,0),(0,0,1),'grey')
sage: t.sphere((4,-1,1), 1, 'mirror')
sage: t.sphere((0,-1,1), 1, 'mirror')
sage: t.sphere((2,-1,1), 0.5, 'mirror')
sage: t.sphere((2,1,1), 0.5, 'mirror')
sage: show(t)

texture_recolor(name, colors)

Recolors default textures.

EXAMPLES:

sage: t = Tachyon()
sage: t.texture('s')
sage: q = t.texture_recolor('s',[(0,0,1)])
sage: t._objects[1]._color
(0, 0, 1)

triangle(vertex_1, vertex_2, vertex_3, texture)

Creates a triangle with the given vertices and texture.

EXAMPLES:

sage: t = Tachyon()
sage: t.texture('s')
sage: t.triangle([1,2,3],[4,5,6],[7,8,10],'s')
sage: t._objects[1]
[1, 2, 3] [4, 5, 6] [7, 8, 10] s

class sage.plot.plot3d.tachyon.TachyonSmoothTriangle(a, b, c, da, db, dc, color=0)

Bases: sage.plot.plot3d.tri_plot.SmoothTriangle

A triangle along with a normal vector, which is used for smoothing.

str()

Returns the scene string for a smoothed triangle.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import TachyonSmoothTriangle
sage: t = TachyonSmoothTriangle([-1,-1,-1],[0,0,0],[1,2,3],[1,0,0],[0,1,0],[0,0,1])
sage: t.str()
'\n        STRI V0  ...  1.0 0.0 0.0  N1  0.0 1.0 0.0   N2  0.0 0.0 1.0 \n             0\n        '

class sage.plot.plot3d.tachyon.TachyonTriangle(a, b, c, color=0)

Bases: sage.plot.plot3d.tri_plot.Triangle

Basic triangle class.

str()

Returns the scene string for a triangle.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import TachyonTriangle
sage: t = TachyonTriangle([-1,-1,-1],[0,0,0],[1,2,3])
sage: t.str()
'\n        TRI V0  -1.0 -1.0 -1.0   V1  0.0 0.0 0.0    V2  1.0 2.0 3.0 \n            0\n        '

class sage.plot.plot3d.tachyon.TachyonTriangleFactory(tach, tex)

Bases: sage.plot.plot3d.tri_plot.TriangleFactory

A class to produce triangles of various rendering types.

get_colors(list)

Returns a list of color labels.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import TachyonTriangleFactory
sage: t = Tachyon()
sage: t.texture('s')
sage: ttf = TachyonTriangleFactory(t, 's')
sage: ttf.get_colors([1])
['SAGETEX1_0']

smooth_triangle(a, b, c, da, db, dc, color=None)

Creates a TachyonSmoothTriangle.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import TachyonTriangleFactory
sage: t = Tachyon()
sage: t.texture('s')
sage: ttf = TachyonTriangleFactory(t, 's')
sage: ttfst = ttf.smooth_triangle([0,0,0],[1,0,0],[0,0,1],[1,1,1],[1,2,3],[-1,-1,2])
sage: ttfst.str()
'\n        STRI V0  0.0 0.0 0.0  ...'

triangle(a, b, c, color=None)

Creates a TachyonTriangle with vertices a, b, and c.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import TachyonTriangleFactory
sage: t = Tachyon()
sage: t.texture('s')
sage: ttf = TachyonTriangleFactory(t, 's')
sage: ttft = ttf.triangle([1,2,3],[3,2,1],[0,2,1])
sage: ttft.str()
'\n        TRI V0  1.0 2.0 3.0   V1  3.0 2.0 1.0    V2  0.0 2.0 1.0 \n            s\n        '

class sage.plot.plot3d.tachyon.Texfunc(type=0, center=(0, 0, 0), rotate=(0, 0, 0), scale=(1, 1, 1))

str()

Returns the scene string for this texture function.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import Texfunc
sage: t = Texfunc()
sage: t.str()
'0 center  0.0 0.0 0.0  rotate  0.0 0.0 0.0  scale  1.0 1.0 1.0 '

class sage.plot.plot3d.tachyon.Texture(name, ambient=0.20000000000000001, diffuse=0.80000000000000004, specular=0.0, opacity=1.0, color=(1.0, 0.0, 0.5), texfunc=0, phong=0, phongsize=0, phongtype='PLASTIC')

recolor(name, color)

Returns a texture with the new given color.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import Texture
sage: t2 = Texture('w')
sage: t2w = t2.recolor('w2', (.1,.2,.3))
sage: t2ws = t2w.str()
sage: color_index = t2ws.find('color')
sage: t2ws[color_index:color_index+20]
'color  0.1 0.2 0.3  '

str()

Returns the scene string for this texture.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import Texture
sage: t = Texture('w')
sage: t.str().split()[2:6]
['ambient', '0.2', 'diffuse', '0.8']

sage.plot.plot3d.tachyon.tostr(s, length=3, out_type=<type 'float'>)

Converts vector information to a space-separated string.

EXAMPLES:

sage: from sage.plot.plot3d.tachyon import tostr
sage: tostr((1,1,1))
' 1.0 1.0 1.0 '
sage: tostr('2 3 2')
'2 3 2'