AUTHORS:
This tutorial outlines the construction of Brandt modules in Sage. The
importance of this construction is that it provides us with a method
to compute modular forms on 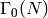 as outlined in Pizer’s paper
[Pi]. In fact there exists a non-canonical Hecke algebra isomorphism
between the Brandt modules and a certain subspace of
as outlined in Pizer’s paper
[Pi]. In fact there exists a non-canonical Hecke algebra isomorphism
between the Brandt modules and a certain subspace of
 which contains all the newforms.
which contains all the newforms.
The Brandt module is the free abelian group on right ideal classes of a quaternion order together with a natural Hecke action determined by Brandt matrices.
A quaternion algebra over  is a central simple algebra of
dimension 4 over
is a central simple algebra of
dimension 4 over  . Such an algebra
. Such an algebra  is said to be
ramified at a place
is said to be
ramified at a place  of
of  if and only if
if and only if 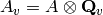 is a division algebra. Otherwise
is a division algebra. Otherwise  is said to be split
at
is said to be split
at  .
.
A = QuaternionAlgebra(p) returns the quaternion algebra  over
over
 ramified precisely at the places
ramified precisely at the places  and
and 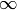 .
.
A = QuaternionAlgebra(k,a,b) returns a quaternion algebra with basis
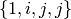 over
over 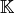 such that
such that 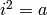 ,
, 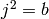 and
and 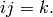
An order 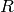 in a quaternion algebra is a 4-dimensional lattice on
in a quaternion algebra is a 4-dimensional lattice on  which is also a subring containing the identity.
which is also a subring containing the identity.
R = A.maximal_order() returns a maximal order 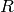 in the quaternion
algebra
in the quaternion
algebra 
An Eichler order 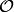 in a quaternion algebra is the
intersection of two maximal orders. The level of
in a quaternion algebra is the
intersection of two maximal orders. The level of 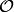 is its
index in any maximal order containing it.
is its
index in any maximal order containing it.
O = A.order_of_level_N returns an Eichler order  in
in  of level
of level  where
where  does not divide
does not divide  .
.
A right 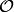 -ideal
-ideal  is a lattice on
is a lattice on  such that
such that
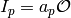 (for some
(for some 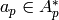 ) for all
) for all 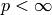 . Two
right
. Two
right 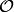 -ideals
-ideals  and
and 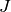 are said to belong to the same
class if
are said to belong to the same
class if 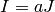 for some
for some 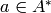 . (Left
. (Left 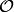 -ideals are
defined in a similar fashion.)
-ideals are
defined in a similar fashion.)
The right order of  is defined to be the set of elements in
is defined to be the set of elements in  which fix
which fix  under right multiplication.
under right multiplication.
right_order (R, basis) returns the right ideal of  in
in 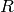 given a
basis for the right ideal
given a
basis for the right ideal  contained in the maximal order
contained in the maximal order 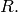
ideal_classes(self) returns a tuple of all right ideal classes in self which, for the purpose of constructing the Brandt module B(p,M), is taken to be an Eichler order of level M.
The implementation of this method is especially interesting. It depends on the construction of a Hecke module defined as a free abelian group on right ideal classes of a quaternion algebra with the following action
where 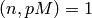 and the sum is over cyclic
and the sum is over cyclic 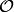 -module
homomorphisms
-module
homomorphisms  up to isomorphism
of
up to isomorphism
of 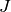 . Equivalently one can sum over the inclusions of the submodules
. Equivalently one can sum over the inclusions of the submodules
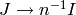 . The rough idea is to start with the trivial
ideal class containing the order
. The rough idea is to start with the trivial
ideal class containing the order 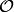 itself. Using the
method cyclic_submodules(self, I, p) one computes
itself. Using the
method cyclic_submodules(self, I, p) one computes ![T_p([\mathcal{O}])](../../../_images/math/4c742d51ea444d1f92a937693eed60771f733cee.png) for some prime integer
for some prime integer  not dividing the level of the order
not dividing the level of the order
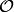 . Apply this method repeatedly and test for equivalence
among resulting ideals. A theorem of Serre asserts that one gets a
complete set of ideal class representatives after a finite number of
repetitions.
. Apply this method repeatedly and test for equivalence
among resulting ideals. A theorem of Serre asserts that one gets a
complete set of ideal class representatives after a finite number of
repetitions.
One can prove that two ideals  and
and 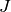 are equivalent if and only
if there exists an element
are equivalent if and only
if there exists an element 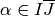 such
such
 .
.
is_equivalent(I,J) returns true if  and
and 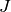 are equivalent. This
method first compares the theta series of
are equivalent. This
method first compares the theta series of  and
and 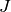 . If they are the
same, it computes the theta series of the lattice
. If they are the
same, it computes the theta series of the lattice 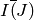 . It
returns true if the
. It
returns true if the 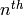 coefficient of this series is nonzero
where
coefficient of this series is nonzero
where 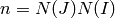 .
.
The theta series of a lattice  over the quaternion algebra
over the quaternion algebra  is
defined as
is
defined as
L.theta_series(T,q) returns a power series representing 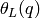 up to a precision of
up to a precision of 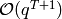 .
.
The Hecke structure defined on the Brandt module is given by the Brandt matrices which can be computed using the definition of the Hecke operators given earlier.
hecke_matrix_from_defn (self,n) returns the matrix of the nth Hecke
operator 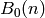 acting on self, computed directly from the
definition.
acting on self, computed directly from the
definition.
However, one can efficiently compute Brandt matrices using theta
series. In fact, let {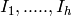 } be a set of right
} be a set of right
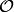 -ideal class representatives. The (i,j) entry in the
Brandt matrix
-ideal class representatives. The (i,j) entry in the
Brandt matrix 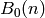 is the product of the
is the product of the 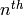 coefficient in
the theta series of the lattice
coefficient in
the theta series of the lattice 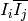 and the first
coefficient in the theta series of the lattice
and the first
coefficient in the theta series of the lattice
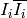 .
.
compute_hecke_matrix_brandt(self,n) returns the nth Hecke matrix, computed using theta series.
sage: B = BrandtModule(23)
sage: B.maximal_order()
Order of Quaternion Algebra (-1, -23) with base ring Rational Field with basis (1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
sage: B.right_ideals()
(Fractional ideal (2 + 2*j, 2*i + 2*k, 4*j, 4*k), Fractional ideal (2 + 2*j, 2*i + 6*k, 8*j, 8*k), Fractional ideal (2 + 10*j + 8*k, 2*i + 8*j + 6*k, 16*j, 16*k))
sage: B.hecke_matrix(2)
[1 2 0]
[1 1 1]
[0 3 0]
sage: B.brandt_series(3)
[1/4 + q + q^2 + O(q^3) 1/4 + q^2 + O(q^3) 1/4 + O(q^3)]
[ 1/2 + 2*q^2 + O(q^3) 1/2 + q + q^2 + O(q^3) 1/2 + 3*q^2 + O(q^3)]
[ 1/6 + O(q^3) 1/6 + q^2 + O(q^3) 1/6 + q + O(q^3)]

We decompose a Brandt module over both  and
and  .:
.:
sage: B = BrandtModule(43, base_ring=ZZ); B
Brandt module of dimension 4 of level 43 of weight 2 over Integer Ring
sage: D = B.decomposition()
sage: D
[
Subspace of dimension 1 of Brandt module of dimension 4 of level 43 of weight 2 over Integer Ring,
Subspace of dimension 1 of Brandt module of dimension 4 of level 43 of weight 2 over Integer Ring,
Subspace of dimension 2 of Brandt module of dimension 4 of level 43 of weight 2 over Integer Ring
]
sage: D[0].basis()
((0, 0, 1, -1),)
sage: D[1].basis()
((1, 2, 2, 2),)
sage: D[2].basis()
((1, 1, -1, -1), (0, 2, -1, -1))
sage: B = BrandtModule(43, base_ring=QQ); B
Brandt module of dimension 4 of level 43 of weight 2 over Rational Field
sage: B.decomposition()[2].basis()
((1, 0, -1/2, -1/2), (0, 1, -1/2, -1/2))
Return the Brandt module of given weight associated to the prime power p^r and integer M, where p and M are coprime.
EXAMPLES:
sage: BrandtModule(17)
Brandt module of dimension 2 of level 17 of weight 2 over Rational Field
sage: BrandtModule(17,15)
Brandt module of dimension 32 of level 17*15 of weight 2 over Rational Field
sage: BrandtModule(3,7)
Brandt module of dimension 2 of level 3*7 of weight 2 over Rational Field
sage: BrandtModule(3,weight=2)
Brandt module of dimension 1 of level 3 of weight 2 over Rational Field
sage: BrandtModule(11, base_ring=ZZ)
Brandt module of dimension 2 of level 11 of weight 2 over Integer Ring
sage: BrandtModule(11, base_ring=QQbar)
Brandt module of dimension 2 of level 11 of weight 2 over Algebraic Field
The use_cache option determines whether the Brandt module returned by this function is cached.:
sage: BrandtModule(37) is BrandtModule(37)
True
sage: BrandtModule(37,use_cache=False) is BrandtModule(37,use_cache=False)
False
TESTS:
Note that N and M must be coprime:
sage: BrandtModule(3,15)
...
ValueError: M must be coprime to N
Only weight 2 is currently implemented:
sage: BrandtModule(3,weight=4)
...
NotImplementedError: weight != 2 not yet implemented
Brandt modules are cached:
sage: B = BrandtModule(3,5,2,ZZ)
sage: B is BrandtModule(3,5,2,ZZ)
True
Bases: sage.modular.hecke.element.HeckeModuleElement
Return the monodromy pairing of self and x.
EXAMPLES:
sage: B = BrandtModule(5,13)
sage: B.monodromy_weights()
(1, 3, 1, 1, 1, 3)
sage: (B.0 + B.1).monodromy_pairing(B.0 + B.1)
4
Bases: sage.modular.hecke.ambient_module.AmbientHeckeModule
A Brandt module.
EXAMPLES:
sage: BrandtModule(3, 10)
Brandt module of dimension 4 of level 3*10 of weight 2 over Rational Field
Return the auxiliary level (prime to p part) of the quaternion order used to compute this Brandt module.
EXAMPLES:
sage: BrandtModule(7,5,2,ZZ).M()
5
Return ramification level N.
EXAMPLES:
sage: BrandtModule(7,5,2,ZZ).N()
7
Return matrix of power series 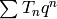 to the given
precision. Note that the Hecke operators in this series are
always over
to the given
precision. Note that the Hecke operators in this series are
always over  , even if the base ring of this Brandt module
is not
, even if the base ring of this Brandt module
is not  .
.
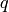 )
)
EXAMPLES:
sage: B = BrandtModule(11)
sage: B.brandt_series(2)
[1/4 + q + O(q^2) 1/4 + O(q^2)]
[ 1/6 + O(q^2) 1/6 + q + O(q^2)]
sage: B.brandt_series(5)
[1/4 + q + q^2 + 2*q^3 + 5*q^4 + O(q^5) 1/4 + 3*q^2 + 3*q^3 + 3*q^4 + O(q^5)]
[ 1/6 + 2*q^2 + 2*q^3 + 2*q^4 + O(q^5) 1/6 + q + q^3 + 4*q^4 + O(q^5)]
Asking for a smaller precision works.:
sage: B.brandt_series(3)
[1/4 + q + q^2 + O(q^3) 1/4 + 3*q^2 + O(q^3)]
[ 1/6 + 2*q^2 + O(q^3) 1/6 + q + O(q^3)]
sage: B.brandt_series(3,var='t')
[1/4 + t + t^2 + O(t^3) 1/4 + 3*t^2 + O(t^3)]
[ 1/6 + 2*t^2 + O(t^3) 1/6 + t + O(t^3)]
Return a list of rescaled versions of the fractional right
ideals 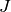 such that
such that 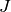 contains
contains  and the quotient has
group structure the product of two cyclic groups of order
and the quotient has
group structure the product of two cyclic groups of order  .
.
We emphasize again that 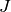 is rescaled to be integral.
is rescaled to be integral.
EXAMPLES:
sage: B = BrandtModule(11)
sage: I = B.order_of_level_N().unit_ideal()
sage: B.cyclic_submodules(I, 2)
[Fractional ideal (1/2 + 3/2*j + k, 1/2*i + j + 1/2*k, 2*j, 2*k),
Fractional ideal (1/2 + 1/2*i + 1/2*j + 1/2*k, i + k, j + k, 2*k),
Fractional ideal (1/2 + 1/2*j + k, 1/2*i + j + 3/2*k, 2*j, 2*k)]
sage: B.cyclic_submodules(I, 3)
[Fractional ideal (1/2 + 1/2*j, 1/2*i + 5/2*k, 3*j, 3*k),
Fractional ideal (1/2 + 3/2*j + 2*k, 1/2*i + 2*j + 3/2*k, 3*j, 3*k),
Fractional ideal (1/2 + 3/2*j + k, 1/2*i + j + 3/2*k, 3*j, 3*k),
Fractional ideal (1/2 + 5/2*j, 1/2*i + 1/2*k, 3*j, 3*k)]
sage: B.cyclic_submodules(I, 11)
...
ValueError: p must be coprime to the level
Return the 1-dimensional subspace of self on which the Hecke
operators 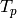 act as
act as 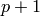 for
for  coprime to the level.
coprime to the level.
NOTE: This function assumes that the base field has characteristic 0.
EXAMPLES:
sage: B = BrandtModule(11); B.eisenstein_subspace()
Subspace of dimension 1 of Brandt module of dimension 2 of level 11 of weight 2 over Rational Field
sage: B.eisenstein_subspace() is B.eisenstein_subspace()
True
sage: BrandtModule(3,11).eisenstein_subspace().basis()
((1, 1),)
sage: BrandtModule(7,10).eisenstein_subspace().basis()
((1, 1, 1, 1/2, 1, 1, 1/2, 1, 1, 1),)
sage: BrandtModule(7,10,base_ring=ZZ).eisenstein_subspace().basis()
((2, 2, 2, 1, 2, 2, 1, 2, 2, 2),)
Return the underlying free module of the Brandt module.
EXAMPLES:
sage: B = BrandtModule(10007,389)
sage: B.free_module()
Vector space of dimension 325196 over Rational Field
Return the matrix of the n-th Hecke operator.
INPUT:
– integer
algorithm – string (default: ‘default’)
- ‘default’ – let Sage guess which algorithm is best
- ‘direct’ – use cyclic subideals (generally much better when you want few Hecke operators and the dimension is very large); uses ‘theta’ if n divides the level.
- ‘brandt’ – use Brandt matrices (generally much better when you want many Hecke operators and the dimension is very small; bad when the dimension is large)
sparse – bool (default: False)
– integer or None (default: None); in direct algorithm, use theta series to this precision as an initial check for equality of ideal classes.
EXAMPLES:
sage: B = BrandtModule(3,7); B.hecke_matrix(2)
[0 3]
[1 2]
sage: B.hecke_matrix(5, algorithm='brandt')
[0 6]
[2 4]
sage: t = B.hecke_matrix(11, algorithm='brandt', sparse=True); t
[ 6 6]
[ 2 10]
sage: type(t)
<type 'sage.matrix.matrix_rational_sparse.Matrix_rational_sparse'>
sage: B.hecke_matrix(19, algorithm='direct', B=2)
[ 8 12]
[ 4 16]
Returns whether self is cuspidal, i.e. has no Eisenstein part.
Return a maximal order in the quaternion algebra associated to this Brandt module.
EXAMPLES:
sage: BrandtModule(17).maximal_order()
Order of Quaternion Algebra (-17, -3) with base ring Rational Field with basis (1/2 + 1/2*j, 1/2*i + 1/2*k, -1/3*j - 1/3*k, k)
sage: BrandtModule(17).maximal_order() is BrandtModule(17).maximal_order()
True
Return the weights for the monodromy pairing on this Brandt
module. The weights are associated to each ideal class in our
fixed choice of basis. The weight of an ideal class ![[I]](../../../_images/math/2547f5530ff0b2e6d9b6e082e5b6302240f54ea5.png) is
half the number of units of the right order
is
half the number of units of the right order  .
.
NOTE: The base ring must be  or
or  .
.
EXAMPLES:
sage: BrandtModule(11).monodromy_weights()
(2, 3)
sage: BrandtModule(37).monodromy_weights()
(1, 1, 1)
sage: BrandtModule(43).monodromy_weights()
(2, 1, 1, 1)
sage: BrandtModule(7,10).monodromy_weights()
(1, 1, 1, 2, 1, 1, 2, 1, 1, 1)
sage: BrandtModule(5,13).monodromy_weights()
(1, 3, 1, 1, 1, 3)
Return Eichler order of level N = p^(2*r+1)*M in the quaternion algebra.
EXAMPLES:
sage: BrandtModule(7).order_of_level_N()
Order of Quaternion Algebra (-1, -7) with base ring Rational Field with basis (1/2 + 1/2*j, 1/2*i + 1/2*k, j, k)
sage: BrandtModule(7,13).order_of_level_N()
Order of Quaternion Algebra (-1, -7) with base ring Rational Field with basis (1/2 + 1/2*j + 12*k, 1/2*i + 9/2*k, j + 11*k, 13*k)
sage: BrandtModule(7,3*17).order_of_level_N()
Order of Quaternion Algebra (-1, -7) with base ring Rational Field with basis (1/2 + 1/2*j + 35*k, 1/2*i + 65/2*k, j + 19*k, 51*k)
Return the quaternion algebra A over QQ ramified precisely at p and infinity used to compute this Brandt module.
EXAMPLES:
sage: BrandtModule(997).quaternion_algebra()
Quaternion Algebra (-2, -997) with base ring Rational Field
sage: BrandtModule(2).quaternion_algebra()
Quaternion Algebra (-1, -1) with base ring Rational Field
sage: BrandtModule(3).quaternion_algebra()
Quaternion Algebra (-1, -3) with base ring Rational Field
sage: BrandtModule(5).quaternion_algebra()
Quaternion Algebra (-2, -5) with base ring Rational Field
sage: BrandtModule(17).quaternion_algebra()
Quaternion Algebra (-17, -3) with base ring Rational Field
Return sorted tuple of representatives for the equivalence classes of right ideals in self.
EXAMPLES:
sage: B = BrandtModule(23)
sage: B.right_ideals()
(Fractional ideal (2 + 2*j, 2*i + 2*k, 4*j, 4*k),
Fractional ideal (2 + 2*j, 2*i + 6*k, 8*j, 8*k),
Fractional ideal (2 + 10*j + 8*k, 2*i + 8*j + 6*k, 16*j, 16*k))
TEST:
sage: B = BrandtModule(1009)
sage: Is = B.right_ideals()
sage: n = len(Is)
sage: prod(not Is[i].is_equivalent(Is[j]) for i in range(n) for j in range(i))
1
Return a basis for the left ideal of R with given generators.
EXAMPLES:
sage: B = BrandtModule(17); A = B.quaternion_algebra(); i,j,k = A.gens()
sage: sage.modular.quatalg.brandt.basis_for_left_ideal(B.maximal_order(), [i+j,i-j,2*k,A(3)])
[1/2 + 1/6*j + 2/3*k, 1/2*i + 1/2*k, 1/3*j + 1/3*k, k]
sage: sage.modular.quatalg.brandt.basis_for_left_ideal(B.maximal_order(), [3*(i+j),3*(i-j),6*k,A(3)])
[3/2 + 1/2*j + 2*k, 3/2*i + 3/2*k, j + k, 3*k]
EXAMPLES:
sage: a = sage.modular.quatalg.brandt.benchmark_magma([(11,1), (37,1), (43,1), (97,1)]) # optional - magma
('magma', 11, 1, ...)
('magma', 37, 1, ...)
('magma', 43, 1, ...)
('magma', 97, 1, ...)
sage: a = sage.modular.quatalg.brandt.benchmark_magma([(11,2), (37,2), (43,2), (97,2)]) # optional - magma
('magma', 11, 2, ...)
('magma', 37, 2, ...)
('magma', 43, 2, ...)
('magma', 97, 2, ...)
EXAMPLES:
sage: a = sage.modular.quatalg.brandt.benchmark_sage([(11,1), (37,1), (43,1), (97,1)])
('sage', 11, 1, ...)
('sage', 37, 1, ...)
('sage', 43, 1, ...)
('sage', 97, 1, ...)
sage: a = sage.modular.quatalg.brandt.benchmark_sage([(11,2), (37,2), (43,2), (97,2)])
('sage', 11, 2, ...)
('sage', 37, 2, ...)
('sage', 43, 2, ...)
('sage', 97, 2, ...)
Return the class number of an order of level N = p^r*M in the quaternion algebra over QQ ramified precisely at p and infinity.
This is an implementation of Theorem 1.12 of [Pizer, 1980].
EXAMPLES:
sage: sage.modular.quatalg.brandt.class_number(389,1,1)
33
sage: sage.modular.quatalg.brandt.class_number(389,1,2) # TODO -- right?
97
sage: sage.modular.quatalg.brandt.class_number(389,3,1) # TODO -- right?
4892713
Return a maximal order in the quaternion algebra ramified at p and infinity.
This is an implementation of Proposition 5.2 of [Pizer, 1980].
EXAMPLES:
sage: A = BrandtModule(17).quaternion_algebra()
sage: sage.modular.quatalg.brandt.maximal_order(A)
Order of Quaternion Algebra (-17, -3) with base ring Rational Field with basis (1/2 + 1/2*j, 1/2*i + 1/2*k, -1/3*j - 1/3*k, k)
Return an order in the quaternion algebra A with given level. (Implemented only when the base field is the rational numbers.)
EXAMPLES:
sage: from sage.modular.quatalg.brandt import quaternion_order_with_given_level, maximal_order
sage: A.<i,j,k> = QuaternionAlgebra(5)
sage: level = 2 * 5 * 17
sage: O = quaternion_order_with_given_level(A, level)
sage: M = maximal_order(A)
sage: L = O.free_module()
sage: N = M.free_module()
sage: print L.index_in(N) == level/5 #check that the order has the right index in the maximal order
True
Given a basis for a left ideal I, return the right order in the quaternion order R of elements such that I*x is contained in I.
EXAMPLES:
We do a consistency check with the ideal equal to a maximal order.:
sage: B = BrandtModule(17); basis = sage.modular.quatalg.brandt.basis_for_left_ideal(B.maximal_order(), B.maximal_order().basis())
sage: sage.modular.quatalg.brandt.right_order(B.maximal_order(), basis)
Order of Quaternion Algebra (-17, -3) with base ring Rational Field with basis (1/2 + 1/6*j + 2/3*k, 1/2*i + 1/2*k, 1/3*j + 1/3*k, k)
sage: basis
[1/2 + 1/6*j + 2/3*k, 1/2*i + 1/2*k, 1/3*j + 1/3*k, k]
sage: B = BrandtModule(17); A = B.quaternion_algebra(); i,j,k = A.gens()
sage: basis = sage.modular.quatalg.brandt.basis_for_left_ideal(B.maximal_order(), [i*j-j])
sage: sage.modular.quatalg.brandt.right_order(B.maximal_order(), basis)
Order of Quaternion Algebra (-17, -3) with base ring Rational Field with basis (1/2 + 1/2*i + 1/2*j + 17/2*k, i, j + 8*k, 9*k)