The module of divisors on the modular curve 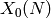 over
over 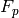 supported at supersingular points.
supported at supersingular points.
AUTHORS:
EXAMPLES:
sage: x = SupersingularModule(389)
sage: m = x.T(2).matrix()
sage: a = m.change_ring(GF(97))
sage: D = a.decomposition()
sage: D[:3]
[
(Vector space of degree 33 and dimension 1 over Finite Field of size 97
Basis matrix:
[ 0 0 0 1 96 96 1 96 96 0 2 96 96 0 1 0 1 2 95 0 1 1 0 1 0 95 0 96 95 1 96 0 2], True),
(Vector space of degree 33 and dimension 1 over Finite Field of size 97
Basis matrix:
[ 0 1 96 75 16 81 22 17 17 0 0 80 80 1 16 40 74 0 0 96 81 23 57 74 0 0 0 24 0 23 73 0 0], True),
(Vector space of degree 33 and dimension 1 over Finite Field of size 97
Basis matrix:
[ 0 1 96 90 90 7 7 6 91 0 0 91 6 13 7 0 91 0 0 84 90 6 0 6 0 0 0 90 0 91 7 0 0], True)
]
sage: len(D)
9
We compute a Hecke operator on a space of huge dimension!:
sage: X = SupersingularModule(next_prime(100000))
sage: t = X.T(2).matrix() # long time (but still less than a minute!)
sage: t.nrows() # long time
8334
TESTS:
sage: X = SupersingularModule(389)
sage: T = X.T(2).matrix().change_ring(QQ)
sage: d = T.decomposition()
sage: len(d)
6
sage: [a[0].dimension() for a in d]
[1, 1, 2, 3, 6, 20]
sage: loads(dumps(X)) == X
True
sage: loads(dumps(d)) == d
True
This function returns a certain quadratic polynomial over a finite field in indeterminate J3.
The roots of the polynomial along with ssJ1 are the neighboring/2-isogenous supersingular j-invariants of ssJ2.
INPUT:
OUTPUT:
EXAMPLES:
The following code snippet produces a factor of the modular polynomial
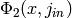 , where
, where 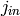 is a supersingular j-invariant
defined over the finite field with
is a supersingular j-invariant
defined over the finite field with 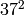 elements:
elements:
sage: F = GF(37^2, 'a')
sage: X = PolynomialRing(F, 'x').gen()
sage: j_in = supersingular_j(F)
sage: poly = sage.modular.ssmod.ssmod.Phi_polys(2,X,j_in)
sage: poly.roots()
[(8, 1), (27*a + 23, 1), (10*a + 20, 1)]
sage: sage.modular.ssmod.ssmod.Phi2_quad(X, F(8), j_in)
x^2 + 31*x + 31
Note
Given a root (j1,j2) to the polynomial 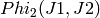 , the pairs
(j2,j3) not equal to (j2,j1) which solve
, the pairs
(j2,j3) not equal to (j2,j1) which solve 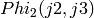 are roots of
the quadratic equation:
are roots of
the quadratic equation:
J3^2 + (-j2^2 + 1488*j2 + (j1 - 162000))*J3 + (-j1 + 1488)*j2^2 + (1488*j1 + 40773375)*j2 + j1^2 - 162000*j1 + 8748000000
This will be of use to extend the 2-isogeny graph, once the initial
three roots are determined for 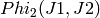 .
.
AUTHORS:
This function returns a certain polynomial of degree 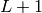 in the
indeterminate x over a finite field.
in the
indeterminate x over a finite field.
The roots of the modular polynomial 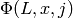 are the
are the
 -isogenous supersingular j-invariants of j.
-isogenous supersingular j-invariants of j.
INPUT:
OUTPUT:
EXAMPLES:
The following code snippet produces the modular polynomial
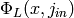 , where
, where 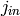 is a supersingular j-invariant
defined over the finite field with
is a supersingular j-invariant
defined over the finite field with 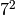 elements:
elements:
sage: F = GF(7^2, 'a')
sage: X = PolynomialRing(F, 'x').gen()
sage: j_in = supersingular_j(F)
sage: sage.modular.ssmod.ssmod.Phi_polys(2,X,j_in)
x^3 + 3*x^2 + 3*x + 1
sage: sage.modular.ssmod.ssmod.Phi_polys(3,X,j_in)
x^4 + 4*x^3 + 6*x^2 + 4*x + 1
sage: sage.modular.ssmod.ssmod.Phi_polys(5,X,j_in)
x^6 + 6*x^5 + x^4 + 6*x^3 + x^2 + 6*x + 1
sage: sage.modular.ssmod.ssmod.Phi_polys(7,X,j_in)
x^8 + x^7 + x + 1
sage: sage.modular.ssmod.ssmod.Phi_polys(11,X,j_in)
x^12 + 5*x^11 + 3*x^10 + 3*x^9 + 5*x^8 + x^7 + x^5 + 5*x^4 + 3*x^3 + 3*x^2 + 5*x + 1
AUTHORS:
Bases: sage.modular.hecke.module.HeckeModule_free_module
The module of supersingular points in a given characteristic, with given level structure.
The characteristic must not divide the level.
NOTE: Currently, only level 1 is implemented.
EXAMPLES:
sage: S = SupersingularModule(17)
sage: S
Module of supersingular points on X_0(1)/F_17 over Integer Ring
sage: S = SupersingularModule(16)
...
ValueError: the argument prime must be a prime number
sage: S = SupersingularModule(prime=17, level=34)
...
ValueError: the argument level must be coprime to the argument prime
sage: S = SupersingularModule(prime=17, level=5)
...
NotImplementedError: supersingular modules of level > 1 not yet implemented
Return the dimension of the space of modular forms of weight 2 and level equal to the level associated to self.
INPUT:
EXAMPLES:
sage: S = SupersingularModule(7)
sage: S.dimension()
1
sage: S = SupersingularModule(15073)
sage: S.dimension()
1256
sage: S = SupersingularModule(83401)
sage: S.dimension()
6950
AUTHORS:
This function returns the 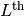 Hecke matrix.
Hecke matrix.
INPUT:
EXAMPLES:
This example computes the action of the Hecke operator 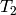 on the module of supersingular points on
on the module of supersingular points on 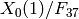 :
:
sage: S = SupersingularModule(37)
sage: M = S.hecke_matrix(2)
sage: M
[1 1 1]
[1 0 2]
[1 2 0]
This example computes the action of the Hecke operator 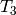 on the module of supersingular points on
on the module of supersingular points on 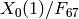 :
:
sage: S = SupersingularModule(67)
sage: M = S.hecke_matrix(3)
sage: M
[0 0 0 0 2 2]
[0 0 1 1 1 1]
[0 1 0 2 0 1]
[0 1 2 0 1 0]
[1 1 0 1 0 1]
[1 1 1 0 1 0]
Note
The first list — list_j — returned by the supersingular_points function are the rows and column indexes of the above hecke matrices and its ordering should be kept in mind when interpreting these matrices.
AUTHORS:
This function returns the level associated to self.
INPUT:
EXAMPLES:
sage: S = SupersingularModule(15073)
sage: S.level()
1
AUTHORS:
This function returns the characteristic of the finite field associated to self.
INPUT:
OUTPUT:
EXAMPLES:
sage: S = SupersingularModule(19)
sage: S.prime()
19
AUTHORS:
Return the dimension of the space of modular forms of weight 2 and level equal to the level associated to self.
INPUT:
EXAMPLES:
sage: S = SupersingularModule(7)
sage: S.dimension()
1
sage: S = SupersingularModule(15073)
sage: S.dimension()
1256
sage: S = SupersingularModule(83401)
sage: S.dimension()
6950
AUTHORS:
This function computes the supersingular j-invariants over the finite field associated to self.
INPUT:
EXAMPLES:
The following examples calculate supersingular j-invariants over finite fields with characteristic 7, 11 and 37:
sage: S = SupersingularModule(7)
sage: S.supersingular_points()
([6], {6: 0})
sage: S = SupersingularModule(11)
sage: S.supersingular_points()
([1, 0], {0: 1, 1: 0})
sage: S = SupersingularModule(37)
sage: S.supersingular_points()
([8, 27*a + 23, 10*a + 20], {8: 0, 10*a + 20: 2, 27*a + 23: 1})
AUTHORS:
Return an upper bound (provably correct) on the number of elliptic curves of conductor equal to the level of this supersingular module.
INPUT:
ALGORITHM: Currently we only use 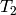 . Function will be
extended to use more Hecke operators later.
. Function will be
extended to use more Hecke operators later.
The prime p is replaced by the smallest prime that doesn’t divide the level.
EXAMPLE:
sage: SupersingularModule(37).upper_bound_on_elliptic_factors()
2
(There are 4 elliptic curves of conductor 37, but only 2 isogeny classes.)
This function returns the weight associated to self.
INPUT:
EXAMPLES:
sage: S = SupersingularModule(19)
sage: S.weight()
2
AUTHORS:
This function returns the dimension of the Supersingular module, which is
equal to the dimension of the space of modular forms of weight  and conductor equal to prime times level.
and conductor equal to prime times level.
INPUT:
EXAMPLES: The code below computes the dimensions of Supersingular modules with level=1 and prime = 7, 15073 and 83401:
sage: dimension_supersingular_module(7)
1
sage: dimension_supersingular_module(15073)
1256
sage: dimension_supersingular_module(83401)
6950
NOTES: The case of level > 1 has not been implemented yet.
AUTHORS:
This function returns a fundamental discriminant  of an
imaginary quadratic field, where the given prime does not split
(see Silverman’s Advanced Topics in the Arithmetic of Elliptic
Curves, page 184, exercise 2.30(d).)
of an
imaginary quadratic field, where the given prime does not split
(see Silverman’s Advanced Topics in the Arithmetic of Elliptic
Curves, page 184, exercise 2.30(d).)
INPUT:
EXAMPLES:
These examples return supersingular discriminants for 7, 15073 and 83401:
sage: supersingular_D(7)
-4
sage: supersingular_D(15073)
-15
sage: supersingular_D(83401)
-7
AUTHORS:
This function returns a supersingular j-invariant over the finite field FF.
INPUT:
EXAMPLES:
The following examples calculate supersingular j-invariants for a few finite fields:
sage: supersingular_j(GF(7^2, 'a'))
6
Observe that in this example the j-invariant is not defined over the prime field:
sage: supersingular_j(GF(15073^2,'a')) # optional -- requires database
10630*a + 6033
sage: supersingular_j(GF(83401^2, 'a'))
67977
AUTHORS: