Heilbronn matrix computation

class sage.modular.modsym.heilbronn.Heilbronn

Bases: object

apply(u, v, N)

Return a list of pairs ((c,d),m), which is obtained as follows: 1) Compute the images (a,b) of the vector (u,v) (mod N) acted on by each of the HeilbronnCremona matrices in self. 2) Reduce each (a,b) to canonical form (c,d) using p1normalize 3) Sort. 4) Create the list ((c,d),m), where m is the number of times that (c,d) appears in the list created in steps 1-3 above. Note that the pairs ((c,d),m) are sorted lexicographically by (c,d).

INPUT:

• u, v, N - integers

OUTPUT: list

EXAMPLES:

sage: H = sage.modular.modsym.heilbronn.HeilbronnCremona(2); H
The Cremona-Heilbronn matrices of determinant 2
sage: H.apply(1,2,7)
[((1, 5), 1), ((1, 6), 1), ((1, 1), 1), ((1, 4), 1)]

to_list()

Return the list of Heilbronn matrices corresponding to self. Each matrix is given as a list of four ints.

EXAMPLES:

sage: H = HeilbronnCremona(2); H
The Cremona-Heilbronn matrices of determinant 2
sage: H.to_list()
[[1, 0, 0, 2], [2, 0, 0, 1], [2, 1, 0, 1], [1, 0, 1, 2]]

class sage.modular.modsym.heilbronn.HeilbronnCremona

Bases: sage.modular.modsym.heilbronn.Heilbronn

p

class sage.modular.modsym.heilbronn.HeilbronnMerel

Bases: sage.modular.modsym.heilbronn.Heilbronn

n

sage.modular.modsym.heilbronn.hecke_images_gamma0_weight2(u, v, N, indices, R)

INPUT:

• u, v, N - integers so that gcd(u,v,N) = 1
• indices - a list of positive integers
• R - matrix over QQ that writes each elements of P1 = P1List(N) in terms of a subset of P1.

OUTPUT: a dense matrix with rational entries whose columns are the images T_n(x) for n in indices and x the Manin symbol (u,v), expressed in terms of the basis.

EXAMPLES:

sage: M = ModularSymbols(23,2,1)
sage: A = sage.modular.modsym.heilbronn.hecke_images_gamma0_weight2(1,0,23,[1..6],M.manin_gens_to_basis())
sage: A
[ 1  0  0]
[ 3  0 -1]
[ 4 -2 -1]
[ 7 -2 -2]
[ 6  0 -2]
[12 -2 -4]
sage: z = M((1,0))
sage: [M.T(n)(z).element() for n in [1..6]]
[(1, 0, 0), (3, 0, -1), (4, -2, -1), (7, -2, -2), (6, 0, -2), (12, -2, -4)]

sage.modular.modsym.heilbronn.hecke_images_gamma0_weight_k(u, v, i, N, k, indices, R)

INPUT:

• u, v, N - integers so that gcd(u,v,N) = 1
• i - integer with 0 = i = k-2
• k - weight
• indices - a list of positive integers
• R - matrix over QQ that writes each elements of P1 = P1List(N) in terms of a subset of P1.

OUTPUT: a dense matrix with rational entries whose columns are the images T_n(x) for n in indices and x the Manin symbol [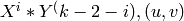], expressed in terms of the basis.

EXAMPLES:

sage: M = ModularSymbols(15,6,sign=-1)
sage: R = M.manin_gens_to_basis()
sage: sage.modular.modsym.heilbronn.hecke_images_gamma0_weight_k(4,1,3,15,6,[1,11,12], R)
[       0        0      1/8     -1/8        0        0        0        0]
[-4435/22 -1483/22     -112 -4459/22  2151/22 -5140/11  4955/22  2340/11]
[ 1253/22  1981/22       -2  3177/22 -1867/22  6560/11 -7549/22  -612/11]
sage: x = M((3,4,1)) ; x.element()
(0, 0, 1/8, -1/8, 0, 0, 0, 0)
sage: M.T(11)(x).element()
(-4435/22, -1483/22, -112, -4459/22, 2151/22, -5140/11, 4955/22, 2340/11)
sage: M.T(12)(x).element()
(1253/22, 1981/22, -2, 3177/22, -1867/22, 6560/11, -7549/22, -612/11)

sage.modular.modsym.heilbronn.hecke_images_nonquad_character_weight2(u, v, N, indices, chi, R)

Return images of the Hecke operators 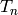for in the list indices, where chi must be a quadratic Dirichlet character with values in QQ.

R is assumed to be the relation matrix of a weight modular symbols space over QQ with character chi.

INPUT:

• u, v, N - integers so that gcd(u,v,N) = 1
• indices - a list of positive integers
• chi - a Dirichlet character that takes values in a nontrivial extension of QQ.
• R - matrix over QQ that writes each elements of P1 = P1List(N) in terms of a subset of P1.

OUTPUT: a dense matrix with entries in the field QQ(chi) (the values of chi) whose columns are the images T_n(x) for n in indices and x the Manin symbol (u,v), expressed in terms of the basis.

EXAMPLES:

sage: chi = DirichletGroup(13).0^2
sage: M = ModularSymbols(chi)
sage: eps = M.character()
sage: R = M.manin_gens_to_basis()
sage: sage.modular.modsym.heilbronn.hecke_images_nonquad_character_weight2(1,0,13,[1,2,6],eps,R)
[           1            0            0            0]
[   zeta6 + 2            0            0           -1]
[           7 -2*zeta6 + 1   -zeta6 - 1     -2*zeta6]
sage: x = M((1,0)); x.element()
(1, 0, 0, 0)
sage: M.T(2)(x).element()
(zeta6 + 2, 0, 0, -1)
sage: M.T(6)(x).element()
(7, -2*zeta6 + 1, -zeta6 - 1, -2*zeta6)

sage.modular.modsym.heilbronn.hecke_images_quad_character_weight2(u, v, N, indices, chi, R)

INPUT:

• u, v, N - integers so that gcd(u,v,N) = 1
• indices - a list of positive integers
• chi - a Dirichlet character that takes values in QQ
• R - matrix over QQ(chi) that writes each elements of P1 = P1List(N) in terms of a subset of P1.

OUTPUT: a dense matrix with entries in the rational field QQ (the values of chi) whose columns are the images T_n(x) for n in indices and x the Manin symbol (u,v), expressed in terms of the basis.

EXAMPLES:

sage: chi = DirichletGroup(29,QQ).0
sage: M = ModularSymbols(chi)
sage: R = M.manin_gens_to_basis()
sage: sage.modular.modsym.heilbronn.hecke_images_quad_character_weight2(2,1,29,[1,3,4],chi,R)
[ 0  0  0  0  0 -1]
[ 0  1  0  1  1  1]
[ 0 -2  0  2 -2 -1]
sage: x = M((2,1)) ; x.element()
(0, 0, 0, 0, 0, -1)
sage: M.T(3)(x).element()
(0, 1, 0, 1, 1, 1)
sage: M.T(4)(x).element()
(0, -2, 0, 2, -2, -1)