Navigation
- index
- modules |
- next |
- previous |
- Sage Reference v4.5.1 »
- Modular Symbols »

Used mainly for computing the cuspidal subspace of modular symbols. The space of boundary symbols of sign 0 is isomorphic as a Hecke module to the dual of the space of Eisenstein series, but this does not give a useful method of computing Eisenstein series, since there is no easy way to extract the constant terms.
We represent boundary modular symbols as a sum of Manin symbols of the form
![[P, u/v]](../../../_images/math/93cd03b4b1c23e61628c1801e789693253034e7b.png) , where
, where 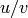 is a cusp for our group
is a cusp for our group  . The group of boundary
modular symbols naturally embeds into a vector space
. The group of boundary
modular symbols naturally embeds into a vector space 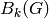 (see Stein,
section 8.4, or Merel, section 1.4, where this space is called
(see Stein,
section 8.4, or Merel, section 1.4, where this space is called ![\CC[\Gamma
\backslash \QQ]_k](../../../_images/math/9433cb91ca5ecebfe507e7221b7e7317570aae53.png) , for a definition), which is a finite dimensional
, for a definition), which is a finite dimensional 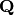 vector space of dimension equal to the number of cusps for
vector space of dimension equal to the number of cusps for  . The embedding
takes
. The embedding
takes ![[P, u/v]](../../../_images/math/93cd03b4b1c23e61628c1801e789693253034e7b.png) to
to ![P(u,v)\cdot [(u,v)]](../../../_images/math/27057f052ed2ee17b5d4fdf435c687662a2be339.png) . We represent the basis vectors by
pairs
. We represent the basis vectors by
pairs ![[(u,v)]](../../../_images/math/899cc458d8d1f1da9406b690e6115ec7e0f8cd4b.png) with u, v coprime. On
with u, v coprime. On 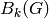 , we have the relations
, we have the relations
![[\gamma \cdot (u,v)] = [(u,v)]](../../../_images/math/95bea2a6787963be1414d79f65e4720c43ccd225.png)
for all 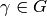 and
and
![[(\lambda u, \lambda v)] = \operatorname{sign}(\lambda)^k [(u,v)]](../../../_images/math/0426b4347f8489b4b05119ea5cd08dccabe652e8.png)
for all 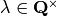 .
.
It’s possible for these relations to kill a class, i.e., for a pair ![[(u,v)]](../../../_images/math/899cc458d8d1f1da9406b690e6115ec7e0f8cd4b.png) to be 0. For example, when
to be 0. For example, when 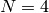 and
and 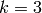 then
then 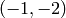 is equivalent mod
is equivalent mod
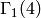 to
to 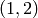 since
since 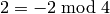 and
and 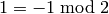 . But since
. But since 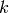 is odd,
is odd, ![[(-1,-2)]](../../../_images/math/4d960a7689c1ec777980b77b5ca6f2e4adb11e8a.png) is also equivalent to
is also equivalent to ![-[(1,2)]](../../../_images/math/05f1bc4ea762682d1dd74e06100ce68463f09b91.png) . Thus this symbol is
equivalent to its negative, hence 0 (notice that this wouldn’t be the case in
characteristic 2). This happens for any irregular cusp when the weight is odd;
there are no irregular cusps on
. Thus this symbol is
equivalent to its negative, hence 0 (notice that this wouldn’t be the case in
characteristic 2). This happens for any irregular cusp when the weight is odd;
there are no irregular cusps on 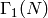 except when
except when 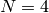 , but there
can be more on
, but there
can be more on 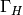 groups. See also prop 2.30 of Stein’s Ph.D. thesis.
groups. See also prop 2.30 of Stein’s Ph.D. thesis.
In addition, in the case that our space is of sign 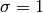 or
or 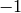 , we
also have the relation
, we
also have the relation ![[(-u,v)] = \sigma \cdot [(u,v)]](../../../_images/math/2dfa347f0cfefcea279d213cce8af851165b534e.png) . This relation can
also combine with the above to kill a cusp class - for instance, take (u,v) =
(1,3) for
. This relation can
also combine with the above to kill a cusp class - for instance, take (u,v) =
(1,3) for 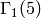 . Then since the cusp
. Then since the cusp  is
is
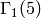 -equivalent to the cusp
-equivalent to the cusp 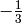 , we have that
, we have that ![[(1,3)] =
[(-1,3)]](../../../_images/math/afd69d8576e4aee886470906b45384ab17261282.png) . Now, on the minus subspace, we also have that
. Now, on the minus subspace, we also have that ![[(-1,3)] = -[(1,3)]](../../../_images/math/e6cdadee1ee1a23403001839c303f382fdc6ca79.png) ,
which means this class must vanish. Notice that this cannot be used to show
that
,
which means this class must vanish. Notice that this cannot be used to show
that ![[(1,0)]](../../../_images/math/005384eaf1021152f7921bf2a923d964820a6c4f.png) or
or ![[(0,1)]](../../../_images/math/945cd54d2ebeb66d6eb1aabb2e2f0a59ad88186f.png) is 0.
is 0.
Note
Special care must be taken when working with the images of the cusps 0 and
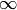 in
in 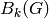 . For all cusps except 0 and
. For all cusps except 0 and 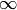 , multiplying the
cusp by -1 corresponds to taking
, multiplying the
cusp by -1 corresponds to taking ![[(u,v)]](../../../_images/math/899cc458d8d1f1da9406b690e6115ec7e0f8cd4b.png) to
to ![[(-u,v)]](../../../_images/math/e41cd6823ce55e4cfc6cf42a95d3defe0fb3a66c.png) in
in 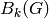 . This
means that
. This
means that ![[(u,v)]](../../../_images/math/899cc458d8d1f1da9406b690e6115ec7e0f8cd4b.png) is equivalent to
is equivalent to ![[(-u,v)]](../../../_images/math/e41cd6823ce55e4cfc6cf42a95d3defe0fb3a66c.png) whenever
whenever  is
equivalent to
is
equivalent to 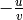 , except in the case of 0 and
, except in the case of 0 and 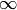 . We
have the following conditions for
. We
have the following conditions for ![[(1,0)]](../../../_images/math/005384eaf1021152f7921bf2a923d964820a6c4f.png) and
and ![[(0,1)]](../../../_images/math/945cd54d2ebeb66d6eb1aabb2e2f0a59ad88186f.png) :
:
![[(0,1)] = \sigma \cdot [(0,1)]](../../../_images/math/77ed6683ad0337194afe8ca8fe527fadc5b9fc07.png) , so
, so ![[(0,1)]](../../../_images/math/945cd54d2ebeb66d6eb1aabb2e2f0a59ad88186f.png) is 0 exactly when
is 0 exactly when 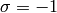 .
.![[(1,0)] = \sigma \cdot [(-1,0)]](../../../_images/math/ec7bce4706ef3eda0c0ebf6026b7c6995457e15b.png) and
and ![[(1,0)] = (-1)^k [(-1,0)]](../../../_images/math/d652a135999cc60dd8217be81dc7f275d182d84c.png) , so
, so
![[(1,0)] = 0](../../../_images/math/ecdb9269c3db413313ce509a01cadc5792083d42.png) whenever
whenever 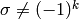 .
.Note
For all the spaces of boundary symbols below, no work is done to determine the cusps for G at creation time. Instead, cusps are added as they are discovered in the course of computation. As a result, the rank of a space can change as a computation proceeds.
REFERENCES:
Bases: sage.modular.hecke.module.HeckeModule_generic
Return the Dirichlet character associated to this space of boundary modular symbols.
EXAMPLES:
sage: ModularSymbols(DirichletGroup(7).0, 6).boundary_space().character()
Dirichlet character modulo 7 of conductor 7 mapping 3 |--> zeta6
Return the underlying free module for self.
EXAMPLES:
sage: B = ModularSymbols(Gamma1(7), 5, sign=-1).boundary_space()
sage: B.free_module()
Sparse vector space of dimension 0 over Rational Field
sage: x = B(Cusp(0)) ; y = B(Cusp(1/7)) ; B.free_module()
Sparse vector space of dimension 2 over Rational Field
Return the i-th generator of this space.
EXAMPLES:
sage: B = ModularSymbols(Gamma0(24), 4).boundary_space()
sage: B.gen(0)
...
ValueError: only 0 generators known for Space of Boundary Modular Symbols for Congruence Subgroup Gamma0(24) of weight 4 and over Rational Field
sage: B(Cusp(1/3))
[1/3]
sage: B.gen(0)
[1/3]
Return the congruence subgroup associated to this space of boundary modular symbols.
EXAMPLES:
sage: ModularSymbols(GammaH(14,[3]), 2).boundary_space().group()
Congruence Subgroup Gamma_H(14) with H generated by [3]
Return True if self is a space of boundary symbols associated to an ambient space of modular symbols.
EXAMPLES:
sage: M = ModularSymbols(Gamma1(6), 4)
sage: M.is_ambient()
True
sage: M.boundary_space().is_ambient()
True
The rank of the space generated by boundary symbols that have been found so far in the course of computing the boundary map.
Warning
This number may change as more elements are coerced into this space!! (This is an implementation detail that will likely change.)
EXAMPLES:
sage: M = ModularSymbols(Gamma0(72), 2) ; B = M.boundary_space()
sage: B.rank()
0
sage: _ = [ B(x) for x in M.basis() ]
sage: B.rank()
16
Return the sign of the complex conjugation involution on this space of boundary modular symbols.
EXAMPLES:
sage: ModularSymbols(13,2,sign=-1).boundary_space().sign()
-1
Return the weight of this space of boundary modular symbols.
EXAMPLES:
sage: ModularSymbols(Gamma1(9), 5).boundary_space().weight()
5
Bases: sage.modular.hecke.element.HeckeModuleElement
Return self as a vector on the QQ-vector space with basis self.parent()._known_cusps().
EXAMPLES:
sage: B = ModularSymbols(18,4,sign=1).boundary_space()
sage: x = B(Cusp(1/2)) ; x
[1/2]
sage: x.coordinate_vector()
(1)
sage: ((18/5)*x).coordinate_vector()
(18/5)
sage: B(Cusp(0))
[0]
sage: x.coordinate_vector()
(1)
sage: x = B(Cusp(1/2)) ; x
[1/2]
sage: x.coordinate_vector()
(1, 0)