Numerical computation of newforms

class sage.modular.modform.numerical.NumericalEigenforms(group, weight=2, eps=9.9999999999999995e-21, delta=0.01, tp=[, 2, 3, 5])

Bases: sage.structure.sage_object.SageObject

numerical_eigenforms(group, weight=2, eps=1e-20, delta=1e-2, tp=[2,3,5])

INPUT:

• group - a congruence subgroup of a Dirichlet character of order 1 or 2
• weight - an integer >= 2
• eps - a small float; abs( ) < eps is what “equal to zero” is interpreted as for floating point numbers.
• delta - a small-ish float; eigenvalues are considered distinct if their difference has absolute value at least delta
• tp - use the Hecke operators T_p for p in tp when searching for a random Hecke operator with distinct Hecke eigenvalues.

OUTPUT:

A numerical eigenforms object, with the following useful methods:

• ap() - return all eigenvalues of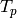

• eigenvalues() - list of eigenvalues corresponding to the given list of primes, e.g.,:

  [[eigenvalues of T_2],
   [eigenvalues of T_3],
   [eigenvalues of T_5], ...]

• systems_of_eigenvalues() - a list of the systems of eigenvalues of eigenforms such that the chosen random linear combination of Hecke operators has multiplicity 1 eigenvalues.

EXAMPLES:

sage: n = numerical_eigenforms(23)
sage: n == loads(dumps(n))
True
sage: n.ap(2)
[3.0, 0.61803398875, -1.61803398875]
sage: n.systems_of_eigenvalues(7)
[
[-1.61803398875, 2.2360679775, -3.2360679775],
[0.61803398875, -2.2360679775, 1.2360679775],
[3.0, 4.0, 6.0]
]
sage: n.systems_of_abs(7)
[
[0.6180339887..., 2.236067977..., 1.236067977...],
[1.6180339887..., 2.236067977..., 3.236067977...],
[3.0, 4.0, 6.0]
]
sage: n.eigenvalues([2,3,5])
[[3.0, 0.61803398875, -1.61803398875],
 [4.0, -2.2360679775, 2.2360679775],
 [6.0, 1.2360679775, -3.2360679775]]

ap(p)

Return a list of the eigenvalues of the Hecke operator 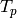on all the computed eigenforms. The eigenvalues match up between one prime and the next.

INPUT:

• p - integer, a prime number

OUTPUT:

• list - a list of double precision complex numbers

EXAMPLES:

sage: n = numerical_eigenforms(11,4)
sage: n.ap(2) # random order
[9.0, 9.0, 2.73205080757, -0.732050807569]
sage: n.ap(3) # random order
[28.0, 28.0, -7.92820323028, 5.92820323028]
sage: m = n.modular_symbols()
sage: x = polygen(QQ, 'x')
sage: m.T(2).charpoly(x).factor()
(x - 9)^2 * (x^2 - 2*x - 2)
sage: m.T(3).charpoly(x).factor()
(x - 28)^2 * (x^2 + 2*x - 47)

eigenvalues(primes)

Return the eigenvalues of the Hecke operators corresponding to the primes in the input list of primes. The eigenvalues match up between one prime and the next.

INPUT:

• primes - a list of primes

OUTPUT:

list of lists of eigenvalues.

EXAMPLES:

sage: n = numerical_eigenforms(1,12)
sage: n.eigenvalues([3,5,13])
[[177148.0, 252.0], [48828126.0, 4830.0], [1.79216039404e+12, -577737.999...]]

level()

Return the level of this set of modular eigenforms.

EXAMPLES:

sage: n = numerical_eigenforms(61) ; n.level()
61

modular_symbols()

Return the space of modular symbols used for computing this set of modular eigenforms.

EXAMPLES:

sage: n = numerical_eigenforms(61) ; n.modular_symbols()
Modular Symbols space of dimension 5 for Gamma_0(61) of weight 2 with sign 1 over Rational Field

systems_of_abs(bound)

Return the absolute values of all systems of eigenvalues for self for primes up to bound.

EXAMPLES:

sage: numerical_eigenforms(61).systems_of_abs(10)
[
[0.311107817466, 2.90321192591, 2.52542756084, 3.21431974338],
[1.0, 2.0, 3.0, 1.0],
[1.48119430409, 0.806063433525, 3.15632517466, 0.675130870567],
[2.17008648663, 1.70927535944, 1.63089761382, 0.460811127189],
[3.0, 4.0, 6.0, 8.0]
]

systems_of_eigenvalues(bound)

Return all systems of eigenvalues for self for primes up to bound.

EXAMPLES:

sage: numerical_eigenforms(61).systems_of_eigenvalues(10)
[
[-1.48119430409..., 0.806063433525..., 3.15632517466..., 0.675130870567...],
[-1.0..., -2.0..., -3.0..., 1.0...],
[0.311107817466..., 2.90321192591..., -2.52542756084..., -3.21431974338...],
[2.17008648663..., -1.70927535944..., -1.63089761382..., -0.460811127189...],
[3.0, 4.0, 6.0, 8.0]
]

weight()

Return the weight of this set of modular eigenforms.

EXAMPLES:

sage: n = numerical_eigenforms(61) ; n.weight()
2

sage.modular.modform.numerical.support(v, eps)

Given a vector and a threshold eps, return all indices where 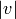is larger than eps.

EXAMPLES:

sage: sage.modular.modform.numerical.support( numerical_eigenforms(61)._easy_vector(), 1.0 )
[]

sage: sage.modular.modform.numerical.support( numerical_eigenforms(61)._easy_vector(), 0.5 )
[0, 1]