Hecke Operators on -expansions

sage.modular.modform.hecke_operator_on_qexp.hecke_operator_on_basis(B, n, k, eps=None, already_echelonized=False)

Given a basis of -expansions for a space of modular forms with character to precision at least 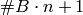, this function computes the matrix of 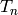relative to .

Note

If the elements of B are not known to sufficient precision, this function will report that the vectors are linearly dependent (since they are to the specified precision).

INPUT:

• B - list of q-expansions
• n - an integer >= 1
• k - an integer
• eps - Dirichlet character
• already_echelonized – bool (default: False); if True, use that the basis is already in Echelon form, which saves a lot of time.

EXAMPLES:

sage: sage.modular.modform.constructor.ModularForms_clear_cache()
sage: ModularForms(1,12).q_expansion_basis()
[
q - 24*q^2 + 252*q^3 - 1472*q^4 + 4830*q^5 + O(q^6),
1 + 65520/691*q + 134250480/691*q^2 + 11606736960/691*q^3 + 274945048560/691*q^4 + 3199218815520/691*q^5 + O(q^6)
]
sage: hecke_operator_on_basis(ModularForms(1,12).q_expansion_basis(), 3, 12)
...
ValueError: The given basis vectors must be linearly independent.

sage: hecke_operator_on_basis(ModularForms(1,12).q_expansion_basis(30), 3, 12)
[   252      0]
[     0 177148]

TESTS:

This shows that the problem with finite fields reported at trac #8281 is solved:

sage: bas_mod5 = [f.change_ring(GF(5)) for f in victor_miller_basis(12, 20)]
sage: hecke_operator_on_basis(bas_mod5, 2, 12)
[4 0]
[0 1]

sage.modular.modform.hecke_operator_on_qexp.hecke_operator_on_qexp(f, n, k, eps=None, prec=None, check=True, _return_list=False)

Given the -expansion of a modular form with character , this function computes the image of under the Hecke operator 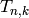of weight .

EXAMPLES:

sage: M = ModularForms(1,12)
sage: hecke_operator_on_qexp(M.basis()[0], 3, 12)
252*q - 6048*q^2 + 63504*q^3 - 370944*q^4 + O(q^5)
sage: hecke_operator_on_qexp(M.basis()[0], 1, 12, prec=7)
q - 24*q^2 + 252*q^3 - 1472*q^4 + 4830*q^5 - 6048*q^6 + O(q^7)
sage: hecke_operator_on_qexp(M.basis()[0], 1, 12)
q - 24*q^2 + 252*q^3 - 1472*q^4 + 4830*q^5 - 6048*q^6 - 16744*q^7 + 84480*q^8 - 113643*q^9 - 115920*q^10 + 534612*q^11 - 370944*q^12 - 577738*q^13 + O(q^14)

sage: M.prec(20)
20
sage: hecke_operator_on_qexp(M.basis()[0], 3, 12)
252*q - 6048*q^2 + 63504*q^3 - 370944*q^4 + 1217160*q^5 - 1524096*q^6 + O(q^7)
sage: hecke_operator_on_qexp(M.basis()[0], 1, 12)
q - 24*q^2 + 252*q^3 - 1472*q^4 + 4830*q^5 - 6048*q^6 - 16744*q^7 + 84480*q^8 - 113643*q^9 - 115920*q^10 + 534612*q^11 - 370944*q^12 - 577738*q^13 + 401856*q^14 + 1217160*q^15 + 987136*q^16 - 6905934*q^17 + 2727432*q^18 + 10661420*q^19 - 7109760*q^20 + O(q^21)

sage: (hecke_operator_on_qexp(M.basis()[0], 1, 12)*252).add_bigoh(7)
252*q - 6048*q^2 + 63504*q^3 - 370944*q^4 + 1217160*q^5 - 1524096*q^6 + O(q^7)

sage: hecke_operator_on_qexp(M.basis()[0], 6, 12)
-6048*q + 145152*q^2 - 1524096*q^3 + O(q^4)

An example on a formal power series:

sage: R.<q> = QQ[[]]
sage: f = q + q^2 + q^3 + q^7 + O(q^8)
sage: hecke_operator_on_qexp(f, 3, 12)
q + O(q^3)
sage: hecke_operator_on_qexp(delta_qexp(24), 3, 12).prec()
8
sage: hecke_operator_on_qexp(delta_qexp(25), 3, 12).prec()
9